Теоретические основы электротехники-3

три коэффициента. Коэффициенты 0, 1, 2 следует выразить через потенциалы узлов (в данном случае вершин) элемента, связав тем самым величины a1, a2,

a3 выражения U(x, y) = 2an n с коэффициентами 0, 1, 2.

n

Решая систему уравнений

U i 0 1xi 2 yi U j 0 1xj 2 yj U k 0 1xk 2 yk

(здесь xi, yi, xj, yj, xk, yk – координаты вершин i, j, k элемента) относительно вели- чин 0, 1, 2, получаем:

где коэффициенты b, c, d определяются через координаты вершин треугольника.

Сопоставление выражений U(x, y) 0 + 1 x + 2 y Ui bi + Uj bj + Uk bk + + (Ui ci + Uj cj + Uk ck) x + (Ui di + Uj dj + Uk dk ) y è U(x, y) ai i(x, y)+ a j j(x, y) + + ak k (x, y) показывает, что ai Ui, aj Uj, ak Uk è i (x, y) bi +ci x + di y,

j (x, y) bj + cj x + dj y, k (x, y) bk + ck x + dk y.

Как видно, базисная функция i (x, y) равна 1 в вершине i элемента и, являясь линейной функцией координат x, y, обращается в нуль в вершинах j, k. Аналогичным свойством характеризуются и базисные функции j (x, y), k (x, y).

В общем случае, когда элемент имеет p узлов, введение матриц

ΓΓ ΓΓò ΓΓ 0, 1, … p ΓΓ, ΓΓ U ΓΓò ΓΓ U1, U2, …Up ,

ΓΓ x ΓΓ ΓΓ 1, x, y, z, x2, y2, … ΓΓ, ΓΓ ΓΓ ΓΓ 1, 2, … pΓΓ

позволяет записать выражение U(x, y) x и после решения уравнения U X ãäå

1, x1, y1, z1, x12 , 1, x2 , y2 , z2 , x22 ,

X

1, x p , y p , z p , x 2p ,

матрица размерностью p p, найти величину X–1 U и выразить потенциал U(x, y) через базисные функции:

U(x, y) x X-1 U U.

Рассмотрим формирование системы уравнений метода конечных элементов при расчете плоскопараллельного электростатического поля.

Рассчитывая производные функционалов всех элементов области по потенциалу узла i и суммируя соответствующие коэффициенты, находим (см. рис. 24.37)

kii 2aiie , kij 2aije , kik 2aike , kil 2aile , kim 2aime , Fi 2 fie .

Таким образом, i-я строка матрицы K системы алгебраических уравнений K U F, получаемая при вычислении производной функционала по потенциалу Ui óçëà i, в данном примере, когда узел i является общим лишь для 5 элемен-

òîâ, ñóòü 0, 0, ...0, kii, kij, kik, kil, kim, kin, 0, ..., 0, 0, åñëè óçëû i, j, k, l, m, n нумерованы один за другим.

Подобно рассмотренному можем рассчитать коэффициенты других строк матрицы K. Она имеет, как правило, не более 10 % ненулевых коэффициентов,

так как производные Je функционалов элементов, которые не включают в себяUi

óçåë i, обращаются в нуль. В связи с тем, что матрица K является редкозаполненной, для решения уравнений метода конечных элементов применяют специальные экономичные методы, учитывающие это свойство системы уравнений.

Решив уравнение KU F, можем рассчитать напряженность поля внутри элементов, а также другие дифференциальные и интегральные характеристики.

Метод конечных элементов применяют при численных расчетах полей в неоднородных, анизотропных и нелинейных средах, когда получение аналитиче- ских решений затруднительно.

Глава двадцать пятая

Расчет электрической емкости

25.1. Емкость между круглыми цилиндрами. Емкость двухпроводной линии передачи

Емкость между двумя уединенными проводящими телами равна отношению заряда q1 q одного из тел к разности их потенциалов U1 – U2; причем предполагается, что заряды тел равны по абсолютному значению и противоположны по знаку, т. е. q2 –q1 –q. Вычисление емкости между двумя телами сводится к вычислению разности их потенциалов в этих условиях. В качестве важного примера найдем выражение для емкости между двумя параллельными круглыми проводящими цилиндрами. Цилиндры будем предполагать бесконечно длинными, емкость будем определять между их отрезками длиной l. В §§ 24.12 и 24.13 было исследовано поле таких цилиндров.

Потенциал в некоторой точке, удаленной на расстояния r1 è r2 от электриче- ских осей цилиндров (см. рис. 24.12 и 24.15), определяется формулой

Нас интересует разность потенциалов самих цилиндров. Для определения потенциалов цилиндров выберем на их поверхностях точки, например наиболее близкие друг к другу точки A1 è A2 (см. рис. 24.14 и 24.15). Пусть k1 — значение отношения r2/r1 для точки A1 и соответственно k2 — значение этого отношения для точки A2. Имеем

Отношение r2/r1 для любой точки поля может быть выражено через радиус R окружности равного потенциала, проходящей через эту точку (см. рис. 24.12), и через расстояние h | x0 | от центра этой окружности до плоскости постоянного потенциала (на рис. 24.12 — до плоскости нулевого потенциала). Воспользовав-

Знак плюс следует брать при k > 1, что соответствует случаю r2 > r1, т. е. расположению окружности равного потенциала слева от плоскости U const (см. рис. 24.15). Знак минус следует брать при k < 1, что соответствует расположению окружности равного потенциала справа от плоскости U const.

Рассмотрим частные случаи.

1. Емкость круглого цилиндра относительно плоскости

(ðèñ. 25.1).

Для плоскости постоянного потенциала k2 r2/r1 1, так как эта плоскость расположена посередине между электрическими осями (см. рис. 24.12). Следовательно,

Здесь h — расстояние от оси цилиндра до плоскости и R — радиус цилиндра. Полученной формулой можно пользоваться для вычисления емкости относительно земли провода, подвешенного на высоте h параллельно поверхности земли. Так как обычно h 00 R, то приближенно

C 1 2l . ln 2h

R

2. Емкость между несоосными, не охватывающими друг друга круглыми цилиндрами (ðèñ. 25.2).

Имеем k1 > 1 è k2 < 1, и, следовательно, перед знаком квадратного корня в формуле для k1 надо взять знак плюс,

Учитывая, что для любого числа x существует тождество

1x 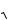x 2 1,

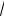xx 2 1

можем переписать формулу для емкости между цилиндрами в виде

86 Часть 4. Теория электромагнитного поля

Величины h1 è h2 определяются через расстояние между геометрическими осями цилиндров и через их радиусы R1 è R2 по формулам:

выведенным в § 24.13.

Для двух цилиндров одинаковых радиусов имеем R1 R2 R è h1 h2 D/2. Формула для емкости при этом принимает вид

3. Емкость между тонкими проводами. Емкость двухпроводной линии переда- чи.

Поэтому формула для емкости может быть представлена в приближенной форме:

5. Емкость между соосными круглыми цилиндрами. Последняя формула переходит в формулу для емкости между соосными цилиндрами в пределе при h1/R1 . è h2/R2 ..

88 Часть 4. Теория электромагнитного поля

Связь между потенциалом U1 òåëà A1 и его зарядом можно выразить в аналогичной форме:

U1 11q1.

Следует подчеркнуть, что коэффициент 11 не равен величине 1/C1, ãäå C1 — емкость тела A1, определяемая в предположении, что все другие тела от него бесконечно удалены. Такое равенство приближенно имеет место только в том случае, когда вносимое тело A2 весьма мало (см. рис. 25.4). В общем случае (см. рис. 25.5) потенциал U1 определяется как зарядом q1, распределенным на поверхности тела A1, так и зарядами, индуцированными на теле A2. Таким образом, коэффициент 11, так же как и коэффициент 21, зависит от формы обоих тел и от их взаимного расположения.

Предположим теперь, что тело A1 имеет суммарный заряд, равный нулю, в то время как заряд q2 òåëà A2 отличен от нуля (рис. 25.6). При этом тела приобретают потенциалы, значения которых про-

В общем случае, когда имеется n заряженных тел: A1, A2, ..., An, получаем систему уравнений:

U1 11q1 12 q2 1k qk 1n qn ; U 2 21q1 22 q2 2k qk 2n qn ;

. . . . . . . . . . . . . . . . .

U k k1q1 k 2 q2 kk qk kn qn ;

. . . . . . . . . . . . . . . . .

U n n1q1 n2 q2 nk qk nn qn .

Коэффициенты носят название п о т е н ц и а л ь н ы х к о э ф ф и ц и е н т о в. Они зависят от формы и размеров поверхностей тел, от взаимного расположения тел и от диэлектрической проницаемости среды. Коэффициенты kk с одинаковыми индексами называются с о б с т в е н н ы м и п о т е н ц и а л ь н ы м и

к о э ф ф и ц и е н т а м и, а коэффициенты nk с различными индексами — в з а - и м н ы м и п о т е н ц и а л ь н ы м и к о э ф ф и ц и е н т а м и. Эти уравнения слу-

жат для вычисления потенциалов тел по заданным их зарядам.

90 Часть 4. Теория электромагнитного поля

Нередко пользуются уравнениями в несколько иной форме, а именно: выражают заряд каждого тела не через потенциалы тел, а через разности потенциалов данного тела и других тел, в том числе и земли. Имеем

q1 C11(U1 0) C12 (U1 U 2 ) C1k (U1 U k ) C1n (U1 U n );

. . . . . . . . . . . . . . . . .

qk Ck1(U k U1) Ck 2 (U k U 2 ) Ckk (U k 0) Ckn (U k U n );

. . . . . . . . . . . . . . . . .

qn Cn1(U n U1) Cn2 (U n U 2 ) Cnk (U n U k ) Cnn (U n 0).

Коэффициенты C в этих уравнениях называются ч а с т и ч н ы м и е м к о - с т я м и — с о б с т в е н н ы м и при одинаковых индексах и в з а и м н ы м и при различных индексах. Для определения собственной частичной емкости Ckk следует принять потенциалы всех тел равными Uk. Тогда qk CkkUk.

Для измерения емкости Ckk необходимо соединить между собой все тела, зарядить всю эту систему до потенциала Uk относительно земли и затем, отключив источник ЭДС, разрядить систему на землю (рис. 25.8). При этом гальванометр должен быть включен так, чтобы был измерен только заряд qk òåëà Ak.

ßñíî, ÷òî Ckk > 0, так как при положительном потенциале системы и заряд на ней будет положителен. При этом же условии U1 U2 ... Uk ... Un из уравнений, содержащих коэффициенты электростатической индукции, имеем

qk (k1 k 2 kk kn )U k .

Следовательно,

Ckk k1 k 2 kk kn .

Взаимная частичная емкость Cnk определяется из того же опыта, что и коэф-

фициент nk. Действительно, при U1 U2 ... Uk–1 Uk+1 ... Un 0 è Uk 0 из уравнений, содержащих частичные емкости, имеем qn – CnkUk. Следовательно,

Cnk – nk. Таким образом, вообще при k p

Ckp – kp è Ckp > 0.

Преимущество уравнений, содержащих частичные емкости, по сравнению с уравнениями, содержащими коэффициенты электростатической индукции, состоит в том, что в них все коэффициенты положительны.

Отметим, что имеет место равенство kp pk, справедливость которого легко доказать из условия независимости энергии системы заряженных тел от последовательности, в которой устанавливаются заряды системы, аналогично тому, как было доказано равенство Mkp Mpk (см. ч. I). Пользуясь определителями, легко показать также, что kp pk. И из условия Ckp – kp следует, что Ckp Cpk. Это соотношение выражает принцип взаимности для системы заряженных тел.