
- •Обращение к читателю
- •Введение
- •РАЗДЕЛ 1. Функции, их свойства и графики
- •§1. Числовые множества
- •§2. Вычисления и расчёты
- •§3. Функциональные зависимости
- •§4. Основные свойства функций
- •§5. Корни n-ой степени
- •§6. Степенные функции с рациональными показателями
- •§7. Основные понятия и аксиомы стереометрии
- •§8. Взаимное расположение двух прямых в пространстве
- •§9. Параллельное проектирование
- •§10. Изображение фигур в стереометрии
- •§11. Параллельность прямых и плоскостей
- •§12. Параллельность плоскостей
- •§13. Тригонометрические функции числового аргумента
- •§14. Основные соотношения между тригонометрическими функциями
- •§15. Свойства и графики тригонометрических функций
- •§16. Тригонометрические формулы сложения и следствия из них
- •§17. Простейшие тригонометрические уравнения и неравенства
- •§18. Перпендикулярность прямой и плоскости
- •§19. Связь между параллельностью и перпендикулярностью прямых и плоскостей
- •§20. Перпендикулярность плоскостей
- •§21. Ортогональное проектирование
- •§23. Измерение расстояний в пространстве
- •§24. Измерение углов в пространстве
- •Ответы и указания к задачам
- •Предметный указатель
- •Содержание

§7. основные понятия и аксиомы стереометрии
Ðассматриваются основные фигуры стереометрии, отношения между ними, их свойства.
 Вы уже знакомы с одним из разделов геометрии —
Вы уже знакомы с одним из разделов геометрии —
планиметрией. В нем изучаются свойства плоских геометрических фигур и отношений между ними.
Но мы живем в пространстве, в котором — три измерения, в отличие от плоскости. Для его восприятия и исследования, для решения практических задач знаний планиметрии недостаточно. Знакомство с геометрией пространства необходимо человеку для его общего развития и профессионального становления.
Геометрия пространства — это математическая наука о пространственных геометрических фигурах, отношениях между ними, а также об их свойствах. Называют ее стереометрией.
Геометрия — греческое γηωμετρια (geometrіa) — зем-
леустройство (землемерие), от γη (ge) или γηa (gea) — земля и μετρεω (metreo) — меряю, измеряю.
Планиметрия — от латинского planum — плоская поверхность, плоскость – и греческого μετρεω — меряю, измеряю.
Стереометрия — от греческих στερεοζ (stereos) —
пространственный и μετρεω — меряю, измеряю.
Возникнув из практики, постоянно обращаясь к ней в процессе своего развития, геометрия стала одной из важнейших математических наук для описания окружающего мира. Основные «действующие лица» в геометрии — геометрические фигуры. Они являются абстракциями объектов реального мира, в которых

130 |
Параллельность прямых и плоскостей |
отображается лишь их форма и размеры. Иначе говоря, геометрические фигуры являются математическими моделями объектов окружающей среды. Так, например, точку в пространстве можно рассматривать как математическую идеализацию реальных объектов — звезд на небе, следа иглы на бумаге, кончика карандаша и т. п. Точка в геометрии не имеет привычных размеров (длины, ширины, высоты). Она применяется для моделирования различных физических тел малых размеров. Безусловно, малых относительно других тел (в некоторых случаях футбольный мяч можно считать точкой, например, на футбольном поле).
Один и тот же предмет может моделироваться различными фигурами в зависимости от цели, которую мы при этом преследуем. Например, можно считать, что крышка данного стола имеет форму прямоугольного параллелепипеда, если нам необходимо найти ее массу, пользуясь плотностью древесины. Но эту крышку можно представлять в форме прямоугольника, если нам необходимо приобрести скатерть.
Геометрические фигуры различаются по своим свойствам, они находятся в различных отношениях между собой: принадлежности, равенства, подобия, параллельности и т. п.
Как и любая наука, геометрия состоит из понятий и утверждений, в которых устанавливаются связи между понятиями. Новые математические понятия определяют через уже известные, а новые утверждения доказывают на основе ранее доказанных. При этом неминуемо возникает вопрос: «А с чего же начинается построение математической теории?». Ответ на этот вопрос найден давно. Еще Евклидом, жившим приблизительно в ІІІ ст. до н.э., создан специальный метод решения данной проблемы. Этот метод называют аксиоматическим. Его сущность заключается в том, что некоторые основные понятия считают неопределяемыми, то есть такими, которым не даются определения. В то же время содержание этих понятий отображают в утверждениях о них, которые считают истинными. Эти утверждения называют аксиомами. По каким причинам признается истинность этих утверждений, в конечном итоге несущественно для построения теории, которую называют аксиоматической теорией. Как правило,
«доверие» к аксиомам вызвано опытом их использования
в практической или научной деятельности.

Основные понятия и аксиомы стереометрии |
131 |
Аксиома — от греческого αξιωομα (axioma) — букваль-
но достоинство, уважение, авторитет — в переносном смысле означает то, что не подлежит сомнению, неопровержимо.
Имея исходный набор первоначальных, неопределяемых понятий, можно начинать построение аксиоматической теории. Таким образом, аксиоматическое построение теории осуществляется по такой схеме:
перечисляются неопределяемые понятия;формулируются аксиомы;
определяются новые понятия с помощью неопределяемых и ранее определённых;
доказываются утверждения на основе аксиом и ранее доказанных утверждений.
Утверждения, которые доказывают в аксиоматической теории, называют теоремами. На практике, для удобства работы с ними, теоремам придают различные названия, отображающие сущность теорем или их роль: свойство, признак, формула, лемма, следствие и т. п.
Теорема — от греческого θεωρημα (theorema), от θεωρεω
(theoreo) — присматриваюсь, наблюдаю — утверждение, истинность которого обосновывают с помощью логических рассуждений, опирающихся на аксиомы, или на ранее доказанные утверждения, или на то и другое.
Полезно аксиоматическое построение математической теории представлять себе в виде некоторой интеллектуальной игры, похожей, например, на игру в шахматы. Шахматы как игра определяется выбором доски, составом фигур и правилами игры. При этом никакого значения не имеют размеры доски, форма фигур, их название, а тем более, из чего они сделаны. Кстати, в шахматы можно играть, фиксируя только ходы на бумаге или в памяти компьютера. Бессмысленно говорить об определении пешки или короля самих по себе. Их сущность проявляется в действиях по отношению к другим фигурам. Примерно так же сущность неопределяемых понятий в аксиоматической теории проявляется в аксиомах. Аксиомы теории, как и правила игры, — это условные соглашения. Целесообразность выбора той или другой аксиомы
132 Параллельность прямых и плоскостей
может быть подтверждена использованием аксиоматической теории в решении тех или иных практических задач.
Чтобы заложить фундамент для изучения стереометрии, нам следует ввести основные (неопределяемые) фигуры стереометрии. Содержание соответствующих им понятий будут выражать свойства, характеризующие отношения между фигурами. Эти свойства принимаются без доказательства, то есть они являются аксиомами стереометрии. На основе аксиом мы сможем доказать новые утверждения, развивающие и дополняющие базовые свойства фигур.
Основными неопределяемыми фигурами стереометрии являются точка, прямая, плоскость. Представление о них вы получили, изучая планиметрию, а содержание соответствующих им понятий будет раскрыто в аксиомах.
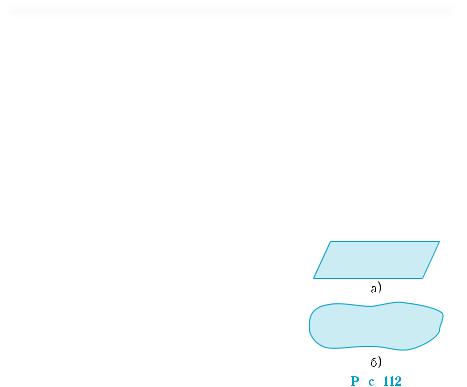
Прежде всего договоримся относительно обозначений и изображений основных фигур. Точка и прямая изображаются и обозначают-
ся так же, как и в планиметрии. Плоскость чаще всего изображают с помощью параллелограмма (рис. 112, а), ведь именно так выглядят самые распространенные физические модели плоскостей: лист бумаги, крышка стола, классная доска и др. Чтобы подчеркнуть
безграничность плоскости, ее иногда изобра- 
 жают как участок «неправильной» формы (рис. 112, б). Плоскости обозначают малыми греческими буквами: α, β, γ и т. п.
жают как участок «неправильной» формы (рис. 112, б). Плоскости обозначают малыми греческими буквами: α, β, γ и т. п.
Наряду с основными неопределяемыми понятиями стереометрии будем считать известным из планиметрии содержание таких понятий, как отрезок и его длина, луч, угол и его ве-
личина и т.п., а также некоторых понятий, характеризующих взаимное расположение точек, прямых и плоскостей: точка
А принадлежит прямой l и плоскости β, прямая l ле-
жит в плоскости α, плоскость α проходит через точку А и др.
Отношения принадлежности точек часто обозначают знаком : М l; М α, а отношение принадлежности прямых — знаком : l α. Запись М α означает, точка М не принадлежит плоскости α. Аналогичное содержание имеет запись l α .
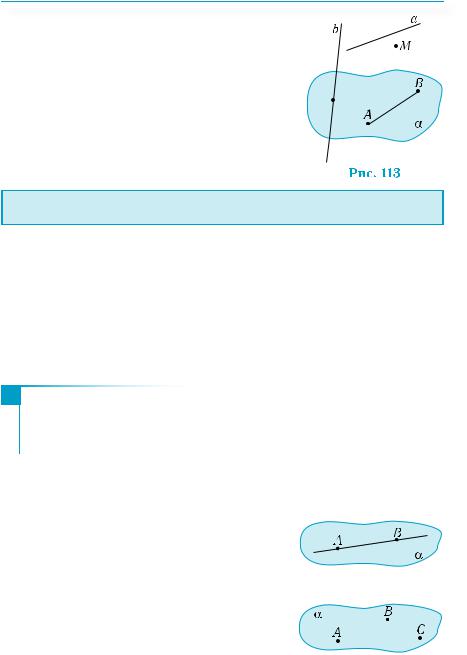
Изображения фигур должны учитывать их взаимное расположение. Например, рис. 113 должен показывать наглядно то, что
Основные понятия и аксиомы стереометрии |
133 |
точка М не принадлежит плоскости α, отрезок АВ лежит в плоскости α, а прямые а и b
не лежат в этой плоскости. Часть прямой b на рис. 113, закрытая изображением плоскости α, обозначена штриховой линией.
Вся совокупность точек, рассматриваемых в стереометрии, образует пространство. Любую часть пространства, то есть некоторую совокупность его точек, называют фи-
гурой.
 Фигура — от латинского figura — образ, вид.
Фигура — от латинского figura — образ, вид.
Фигура называется плоской, если все ее точки размещены в одной плоскости. Со многими плоскими фигурами вы уже ознакомились, изучая планиметрию. Некоторые неплоские фигуры — куб, шар, цилиндр — также известны вам.
Если различные фигуры имеют общие точки, то говорят, что они пересекаются. Поэтому выражение «плоскости пересекаются» означает, что у этих плоскостей есть общие точки. Пересечение, то есть общую часть фигур, обозначают знаком ∩:
l∩ α,α ∩β.
!Будемисходитьизтого,чтопространствовстереометрии содержит бесконечное множество плоскостей. То есть вне каждой плоскости существует бесконечное множество плоскостей, а вместе с этим и точек, и прямых.
Рассмотрим основные свойства, характеризующие неопределяемое понятие плоскости и его связи с другими основными понятиями.
С1. Если прямая проходит через две точки данной плоскости, то она полностью лежит в этой плоскости.
C2. Через три точки, не лежащие на одной прямой, проходит одна и только одна плоскость.
134 |
Параллельность прямых и плоскостей |
С3. Если две различные плоскости имеют общую точку, то их пересечением является прямая, проходящая через эту точку.
C4. Через две произвольные точки пространства можно провести одну и только одну прямую.
Эти свойства, с учетом сделанных выше предположений, и примем за систему аксиом нашего курса стереометрии.
Содержание аксиом хорошо согласуется со свойствами физических объектов и величин, моделируемых с помощью основных геометрических понятий. Действительно, попробуйте прижать к столу концы хорошо натянутой нити и увидите, что она плотно прилегает к поверхности стола, сливается с ней. Именно такое свойство моделирует аксиома С1.
На трех ножках стол стоит, не качаясь, даже если они имеют разную высоту. Устойчивость такого стола объясняется тем, что концы трех его ножек всегда размещаются в плоскости пола и даже определяют ее (аксиома С2). Зато стол с четырьмя ножками иногда может качаться. Аксиома С2 указывает на один из способов задания плоскости. Понятно, что плоскость однозначно определяют прямая и точка, которая лежит вне этой прямой, две пересекающиеся прямые. Обоснование этих утверждений будет приведено дальше. Равносильность указанных способов задания плоскостей естественна: имея три точки, не лежащие на одной прямой, можно построить пересекающиеся прямые (даже три пары пересекающихся прямых), две пересекающиеся прямые позволяют выбрать три точки, не лежащие на одной прямой, и т. д.
Нас окружают многочисленные проявления аксиомы С3: по прямой пересекаются много плоских объектов (стены комнаты, детали ящика и т. п.).
Легко найти и физические аналоги аксиомы С4. Ведь, например, две натянутые нити сливаются, если их концы совпадают.

Основные понятия и аксиомы стереометрии |
135 |
Изучая стереометрию, будем широко использовать соответствиемеждуобъектамиреальногомира,отношениямимеждуними и их геометрическими образами и отношениями между ними. Это соответствие будет служить не только иллюстрацией геометрических понятий и фактов, а даже и неформальным обоснованием их содержательности. При этом следует иметь в виду, что строгие доказательства утверждений существуют и при определенных усилиях могут быть построены.
Отметим также, что стереометрия имеет много аналогий в планиметрии. В частности, подобно тому, как прямая на плоскости разбивает ее на две полуплоскости,
!пространство разбивается каждой плоскостью на два полупространства, причем точки А, В принадлежат одному полупространству тогда и только тогда, когда отрезок АВ не пересекает данную плоскость. Будем считать также, что на каждой плоскости пространства можно пользоваться известными понятиями и фактами планиметрии.
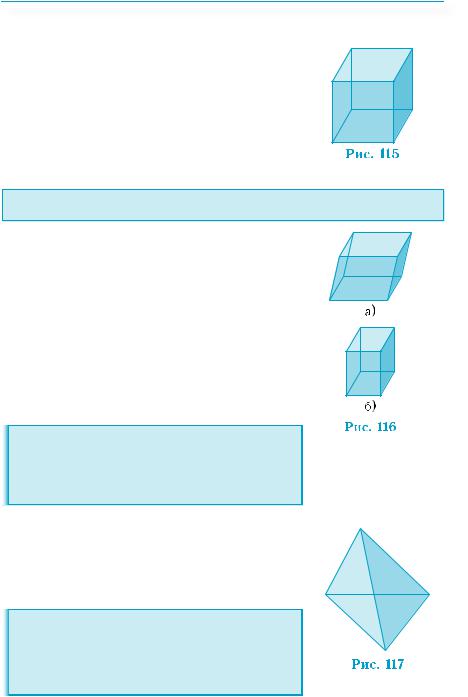
Понятия точки, прямой, плоскости и т. п. относятся к основным в стереометрии, так как с них начинается ее построение. Но главной целью стереометрии является изучение сугубо пространственных фигур. Поэтому, чтобы сделать построение стереометрии содержательнее, мы с самого начала будем использовать некоторые простые пространственные фигуры — куб, параллелепипед, пирамиду, шар и др. (рис. 114), отложив их детальное изучение на будущее. Эти фигуры вы уже неоднократно рассматривали, начиная с младших классов.
136 |
Параллельность прямых и плоскостей |
Вспомним, прежде всего, о некоторых многогранниках, представляющих собой части пространства, ограниченные многоугольниками. Многоугольники, ограничивающие многогранник, называют его гранями, их стороны — рёбрами, а
вершины — вершинами многогранника. Куб — это многогранник, имещий 6 граней и все они являются квадратами. У него
8 вершин и 12 рёбер (рис. 115).
 Куб — от греческого χνβοζ (kіbоs) — игральная кость.
Куб — от греческого χνβοζ (kіbоs) — игральная кость.
Параллелепипед — это многогран-
ник, имеющий 6 граней, и все они —
параллелограммы, и такое же количество
вершин и рёбер, как куб (рис. 116, а). Па-
раллелепипед, все грани которого яв-
ляются прямоугольниками, называется |
|
прямоугольным |
параллелепипедом |
(рис. 116, б). |
|
Куб является частным случаем прямоугольного параллелепипеда. Его грани не только прямоугольники, но даже квадраты.
Параллелепипед — от греческих
παραλληλοζ (parallelos) — параллельный и επιπεδοζ (epipedos) — равное,
плоское.
Тетраэдр — это многогранник, имеющий 4 грани, являющиеся треугольниками (рис. 117). Если все грани тетраэдра – правильные треугольники, то тетраэдр называется правильным тетраэдром.
Тетраэдр — от греческих τετραζ
(tetras) — четыре, в сложных словах
τετρα - (tetra-) и εζρα (hedra) — осно-
вание, поверхность, сторона.
Основные понятия и аксиомы стереометрии |
137 |
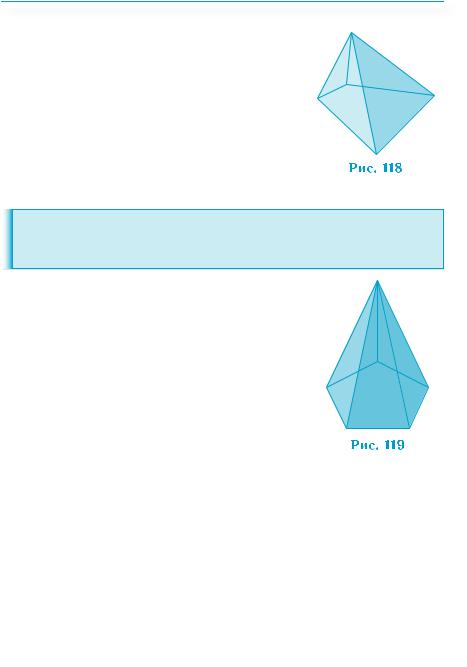
Пирамида — это многогранник, у которого одна грань — произвольный многоугольник, а остальные грани — треугольники с общей вершиной (рис. 118). Первая грань называется основанием, а остальные — боковыми гранями, их общая вершина — вершиной пирамиды. Рёбра, сходящиеся в вершине пирамиды, называют боковыми. Тетраэдр является частным случаем пирамиды. Каждая его грань может служить основанием.
Пирамида — от греческого πνραμιζ (руrатіs), по-
видимому, от египетского рereтиs — диагональ основания.
Если основанием пирамиды служит п-угольник, то она называется п-угольной. Если основанием пирамиды является правильный п-угольник, а боковые грани — равные равнобедренные треугольники с вершинами в вершине пирамиды, то пирамида называется правильной п-уголь- ной. Изображается она при п = 5 так, как показано на рис. 119. Правильный тетраэдр является частным случаем правильной треугольной пирамиды.
Шар с центром в точке О радиуса
R — это множество точек пространства, находящихся от точки О на расстоянии, не превышающем R (рис. 120).
Итак, имеем ряд основных понятий и аксиом сте- 
 реометрии. Построение теории начнем с доказательства утверждения, равнозначного по содержанию аксиоме С2. Эта аксиома определяет один из
реометрии. Построение теории начнем с доказательства утверждения, равнозначного по содержанию аксиоме С2. Эта аксиома определяет один из
способов задания плоскости в пространстве, что, кстати, позволя-
138 |
Параллельность прямых и плоскостей |
ет плоскость, определяемую точками А, В, С, называть плоскостью АВС. Однако с помощью точек и прямых плоскость можно задать иначе. Опыт подсказывает, что плоскость однозначно определяется прямой и точкой вне её или же двумя пересекающимися прямыми. Согласно правилам построения стереометрии на аксиоматической основе, эти утверждения необходимо доказать, исходя из аксиом.
Теорема 1 (о плоскости, проходящей через прямую и точку).
Через прямую и точку, не лежащую на этой прямой, проходит плоскость и к тому же только одна.
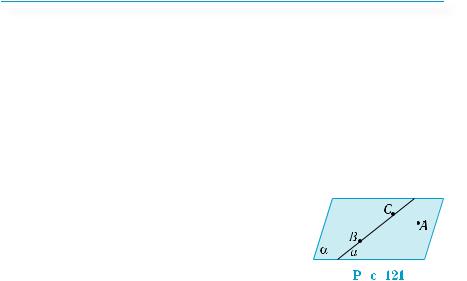
Пусть даны прямая а и точка А, не лежащая на этой прямой. Возьмем на прямой а две точки В и С (рис. 121). Согласно аксиоме С4, прямая а — единственная прямая, проходящая через точки В и С.
Поскольку точка А, по условию теоремы, 
 не принадлежит прямой а, то точки А, В и С не могут лежать на одной прямой.
не принадлежит прямой а, то точки А, В и С не могут лежать на одной прямой.
Согласно аксиоме С2, существует плоскость α, содержащая точки А, В, С, и, в соответствии с аксиомой С1, эта плоскость содержит прямую а. Следовательно, искомая плоскость существует.
Любая другая плоскость β, проходящая через прямую а и точку А, содержит точки В и С. Так как через точки А, В, С можно провести лишь одну плоскость (аксиома С2), то плоскость β совпадает с α. А это значит, что искомая плоскость — единственная.
Анализируя доказательство теоремы, нетрудно прийти к выводу, что через каждую прямую проходит бесконечное множество плоскостей. Расположение каждой из них определяется некоторой точкой, не лежащей на данной прямой. Это можно проиллюстрировать, например, вращая двери относительно неподвижных навесов. Еще один способ задания плоскости сформулирован в следующей теореме.
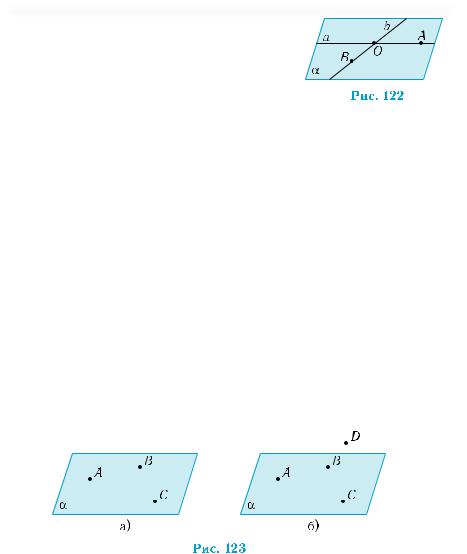
Теорема 2 (о плоскости, проходящей через две пересекающиеся прямые).
Через две пересекающиеся прямые проходит плоскость и притом лишь одна.
Пусть прямые а и b имеют одну общую точку О. Возьмём на этих прямых произвольные точки А и В, отличные от О (рис. 122).
Основные понятия и аксиомы стереометрии |
139 |
Точки А, О, В не лежат на одной прямой, поэтому существует плоскость α, содержа-
щая эти точки (аксиома С2). Плоскость α содержит прямые а и b (аксиома С1). Следовательно, через данные прямые проходит плоскость.
Каждая иная плоскость β, проходящая через прямые а и b, содержит точки А, О, В, и, согласно аксиоме С2, должна совпадать с плоскостью α, поскольку эти точки не лежат на одной прямой.
Следующая задача содержит утверждение, которое будет широко использоваться при последующем изучении стереометрии.
Задача 1. Доказать, что в пространстве существуют четыре точки, не лежащие в одной плоскости.
Необходимо доказать существование четырех точек, которые нельзя поместить в одну плоскость, то есть, что не существует плоскости, проходящей через эти четыре точки.
Возьмем произвольную плоскость α и в ней выберем три точки А, В, С, не лежащие на одной прямой (рис. 123, а). Поскольку вне плоскости α существуют точки пространства, то выберем из них произвольную точку D (рис. 123, б). Не существует плоскости β, которая содержала бы точки А, В, С, D. В противном случае плоскости α и β совпадали бы (по аксиоме С2), и точка D принадлежала бы плоскости α.
Вприведенных аксиомах и теоремах шла речь о прямых
иплоскостях, задаваемых тем или иным способом. Нам и дальше придется строить в пространстве различные фигуры, опираясь на их свойства. Задачи на построение в стереометрии аналогичны задачам на построение в планиметрии. Однако, в стереометрии нет инструментария для построения плоскости. Да и изображение пространственных построений на плоском рисунке не всегда
140 |
Параллельность прямых и плоскостей |
адекватно воспроизводит реальность. Поэтому в стереометрии под построением понимают доказательство возможности всех шагов процесса построения. При этом считается, что плоскость построена, если определены три точки, не лежащие на одной прямой, или прямая и точка вне прямой, или две пересекающиеся прямые, или же другие элементы, определяющие плоскость. Для построения прямой достаточно иметь две ее точки.
Естественно считать, что на каждой плоскости возможны
все построения, известные из планиметрии.
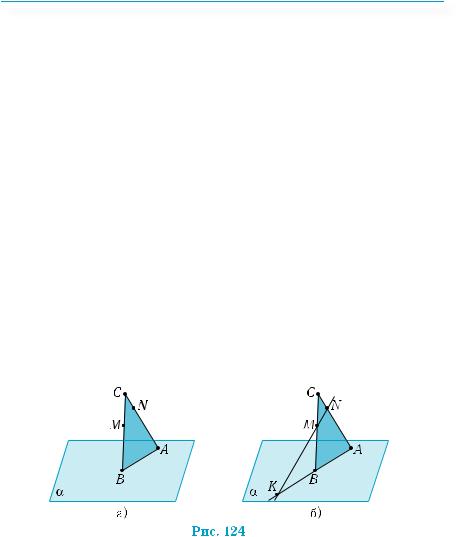
Пример 1. Сторона АВ треугольника АВС лежит в плоскости α, а вершина С — вне её. Точка M делит отрезок СВ в отношении 3 : 4, а точка N делит отрезок СА в отношении 1 : 4, считая от С. Построить точку пересечения прямой MN с плоскостью α.
Условиям примера соответствует рис. 124, а). Прямая MN лежит в плоскости АВС. Пересечением этой плоскости с плоскостью α является прямая АВ. Поэтому искомая точка пересечения расположена на прямой АВ. Прямые АВ и MN лежат в плоскости АВС и, как это вытекает из условия, пересекаются. Найдем их точку пересечения, продлив отрезки АВ и NМ до пересечения в точке K (рис. 124, б). Она и является искомой точкой пересечения прямой МN и плоскости α.
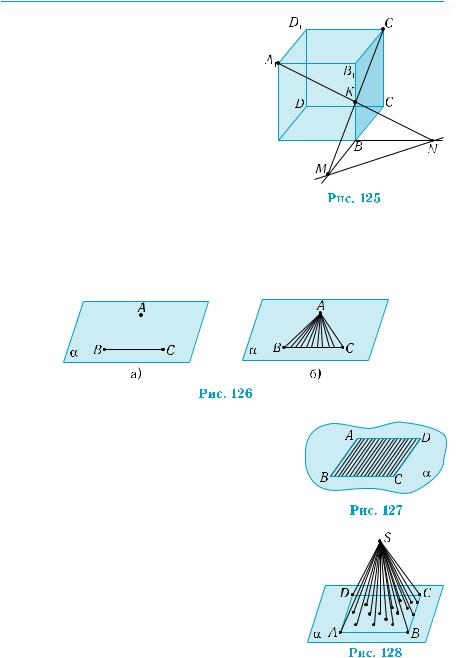
Пример 2. Построить линию пересечения плоскости, проходящей через вершины А1, С1 куба АBCDA1B1C1D1 и середину K ребра BB1, с плоскостью грани АBСD.
Чтобы построить искомую прямую пересечения, достаточно найти две ее точки. Для нахождения этих точек воспользуемся решением примера 1. Поскольку прямая С1K лежит в плоскости грани BCC1B1, то точка М пересечения прямых С1K и СВ является
Основные понятия и аксиомы стереометрии |
141 |
одной из точек искомой прямой пересечения (рис. 125), а вторая точка N является точкой пересечения прямых АB и A1K в плоскости грани АBB1A1. Прямая МN является искомой.
Для введения геометрических фигур, как плоских, так и пространс-
твенных, можно применять конс- 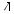 труктивный подход. Этот подход предусматривает построение фигур из отрезков. Продемонстрируем его на следующих примерах.
труктивный подход. Этот подход предусматривает построение фигур из отрезков. Продемонстрируем его на следующих примерах.
Пусть в некоторой плоскости α имеем отрезок ВС и точку А, лежащую вне прямой ВС (рис. 126, а). Соединим отрезками все точки отрезка ВС с точкой А (рис. 126, б). Фигура, состоящая из точек всех построенных отрезков, является треугольником.
Если же имеем отрезок ВС и по одну сторону от прямой ВС отложим от каждой точки отрезка равные и параллельные между собой отрезки (рис. 127), то концы этих отрезков образуют отрезок AD (докажите!), а фигура, образованная из всех точек этих отрезков, является параллелограммом.
Теперь понятно, как в пространстве можно конструктивно ввести некоторые фигуры, например, пирамиды, в частности тетраэдры.
Возьмем четырехугольник ABCD в плоскостиα,атакжеточкуS внеплоскостиα.Соединим точку S со всеми точками четырёхугольника ABCD (рис. 128).
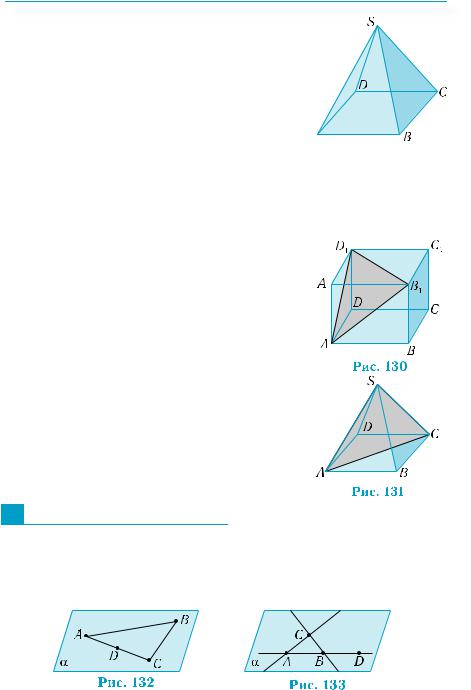
142 Параллельность прямых и плоскостей
Совокупность всех точек отрезков, соединяющих точку S с точками четырехугольника ABCD, образует фигуру, которая яв-
ляется четырехугольной пирамидой.
Обычно четырехугольную пирамиду изображают, как это сделано на рис. 129.
Аналогично строят пирамиды, основаниями которых служат многоугольники с про- 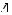
извольным числом сторон. 


 Для изучения пространственных фигур целесообразно рас-
Для изучения пространственных фигур целесообразно рас-
сматривать пересечения этих фигур с плоскостями. Такие пересечения называются сечениями, если по обе стороны от плоскости пересечения — секущей плоскости — есть точки фигуры.
Нетрудно убедиться в том, что сечениями параллелепипеда или пирамиды являются многоугольники. Действительно, из аксиомы
C3 вытекает, что пересечением секущей плоскости и грани фигуры является отрезок.
Таким образом, при пересечении данных фигур с плоскостью получим ограниченные отрезками фигуры на плоскости, то
есть многоугольники. Так, сечением куба ABCDA1B1C1D1 (рис. 130) плоскостью, про-
ходящей через вершины А, В1, D1, является
треугольник AB1D1, а сечением пирамиды
SABCD плоскостью, проходящей через вер-
шину S и диагональ основания AC является
треугольник ASC (рис. 131).
Контрольные вопросы
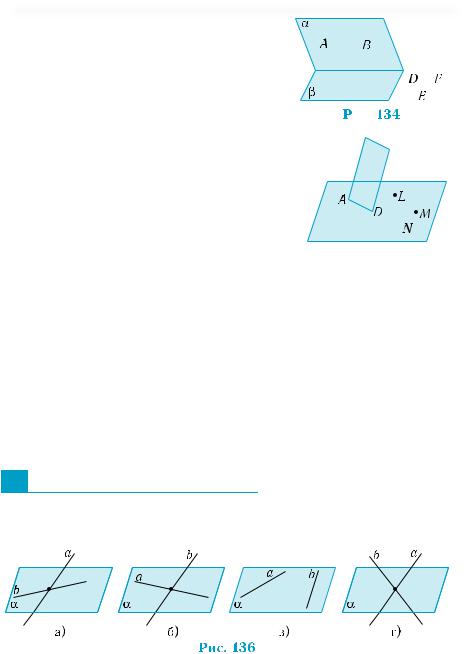
1.Какими тремя точками, указанными на рис. 132, плоскость α определяется однозначно?
2.Через какие три точки, указанные на рис. 133, можно провести еще одну плоскость, отличающуюся от плоскости α?
Основные понятия и аксиомы стереометрии |
143 |
3.Какая из точек D, Е, F на рис. 134 мо-
жет быть точкой пересечения прямой 
иплоскости β?  Четырехугольник АВСD — паралле-
Четырехугольник АВСD — паралле-  лограмм, K CD. Какая из точек L, М,
лограмм, K CD. Какая из точек L, М, 
на рис. 135 может быть точкой пере-
сечения прямой ВK с плоскостью α? 
 Две вершины треугольника прина-
Две вершины треугольника прина-  длежат плоскости. Принадлежит ли ей
длежат плоскости. Принадлежит ли ей  третья вершина?
третья вершина?  Всегда ли через три точки можно провести единственную плоскость?
Всегда ли через три точки можно провести единственную плоскость?
Можно ли утверждать, что один из диаметров окружности принадлежит плос- 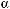

кости, если две точки этой окружности 


 принадлежат этой плоскости?
принадлежат этой плоскости?
Чтобы придать устойчивость геодезическим (теодолитам, нивелирам и т. п.), их обычно треногах. Почему?
На сколько частей делят пространство три плоскости они имеют ровно одну общую точку?
Всегда ли через четыре точки можно провести плоскость Столяр с помощью линейки проверяет, хорошо ли отшлифо вана поверхность. Как он это делает?
Можно ли торт разрезать на восемь частей, сделав лишь три
разреза?4.8.9.7.6.5. АВN инструментамзакрепляют на, если10. ?11. -12.
Графические упражнения
1. Укажите взаимное расположение прямых а, b и плоскости α, изображенных на рис. 136, а)-г).
144 |
Параллельность прямых и плоскостей |
|
2. На рис. 137 прямая AB не принадлежит |
|
|
плоскости COD. |
|
|
1) Сколько общих точек имеют плоскости |
|
|
AOB и COD? |
|
|
2) |
Какая фигура является пересечением |
|
плоскостей AOC и BOD? |
|
|
3) |
Сколько плоскостей можно провести |
|
через точки А, В, С? |
|
|
3. На рис. 138 изображен прямоугольный параллелепипед. |
||
1) Сколько плоскостей можно провести через вершины A, D1, C? |
||
2) |
Сколько плоскостей можно провести через вершины A, C |
|
и середину отрезка BD? |
|
|
3) |
Какая фигура является пересечением плоскостей АВС |
|
и C1D1D? |
|
|
4) |
Сколько общих точек имеют плоскости BCD и АСВ1? |
и T не |
4. Какие из следующих пар точек X и Y, X и Z, Y и T, Z |
||
лежат в одной грани тетраэдра, изображенного на рис. 139? |
||
5. На рис. 140 изображены плоскости AED и AFB. |
|
|
1) |
Какая фигура является их пересечением? |
|
2) |
Сколько плоскостей можно провести через точки F, C, Е? |
|
3) |
Сколько плоскостей можно провести через точки А, Е, F? |
|
4)КакаяпрямаяявляетсяпересечениемплоскостейBCD иЕАС? |
||
6. Постройте рисунок, используя приведенные данные. |
|
|
1) |
Плоскость α проходит через прямую а и точку М, не лежа- |
|
щую на прямой а, и пересекает прямую с в точке М. |
|
|
2) |
Прямые МС и МВ пересекают плоскость α в одной точке. |
|
3)ПрямыеМСиМВпересекаютплоскостьαвразличныхточках. |
||
4) Плоскости α и β пересекаются по прямой l. Прямая а |
лежит |
|
в плоскости α, а прямая b — в плоскости β, прямые а |
и b не |
|
имеют общих точек. |
|
|

Основные понятия и аксиомы стереометрии |
145 |
Задачи
118.Докажите, что через каждую прямую можно провести: 1°) две различные плоскости;
2)бесконечное множество различных плоскостей.
119.Докажите,чтовсепрямые,пересекающиеданнуюпрямуюипроходящиечерезданнуюточку,расположеннуювнепрямой:
1°) находятся в одной плоскости;
2)образуютплоскостьсудалённойпрямой,кромеданнойточки. 120°. Докажите, что если четыре точки не лежат в одной плоскости, то никакие две прямые, попарно соединяющие эти точ-
ки, не пересекаются.
121°. Докажите, что если четыре точки не лежат в одной плоскости, то никакие три из них не лежат на одной прямой.
122°. Две смежные вершины и точка пересечения диагоналей трапеции лежат в плоскости α. Докажите, что и другие две вершины трапеции лежат в плоскости α.
123.Точка D расположена вне плоскости треугольника ABC, N — середина отрезка DC. Докажите, что прямые BN и AC не имеют общих точек.
124.Дан куб ABCDA1B1C1D1 и точка М на ребре ВВ1, не совпадающая с его концами. На какой прямой лежит точка пересечения прямой:
1°) МС с плоскостью А1В1D1; 2°) АМ с плоскостью В1С1D1; 3°) MA1 с плоскостью ABD; 4°) A1M с плоскостью BCD; 5) МD1 с плоскостью АВС; 6) DM с плоскостью A1C1D1?
125.Плоскости α и β пересекаются по прямой с. Отрезок АВ лежит в плоскости α и не параллелен прямой с. Постройте точку пересечения прямой АВ с плоскостью β.
Плоскости α и β пересекаются по прямой l. Точки A и С лежат в плоскости α, причем прямая АС не параллельна прямой l, а точка В лежит в плоскости β. Постройте линии пересечения плоскости АВС с плоскостями α и β.
Точки А, L, K лежат по одну сторону от плоскости α. Прямая пересекает плоскость α в точке В, а прямая LK — в точке Постройте точку пересечения прямой АK с плоскостью α.
128.Двеплоскостиαиβпересекаютсяпопрямойт.Прямаяалежит в плоскости α, прямая b — в плоскости β. Эти прямые пересекаютсявточкеА.Докажите,чтоточкаАлежитнапрямойт.

146 |
Параллельность прямых и плоскостей |
129.Плоскость γ пересекает плоскости α и β по прямым a и b соответственно. Докажите, что если прямые a и b пересекаются, то точка их пересечения лежит на линии пересечения плоскостей α и β.
Даны две прямые, не лежащие в одной плоскости. Через каждую из них проведена плоскость, пересекающая другую прямую. Докажите, что проведенные плоскости пересекаются по прямой, пересекающей каждую из данных прямых.
Фигура состоит не менее чем из двух точек и обладает таким свойством,чтопрямая,соединяющаядвееепроизвольныеточки, полностьюпринадлежитэтойфигуре.Докажите,чтоданнаяфигураможетбытьлишьпрямой,плоскостьюилипространством.
132.Постройте сечение куба ABCDA1B1C1D1 плоскостью, проходящей через:
1°) прямую А1С1 и точку В; 2°) точки B, D, C1; 3°) прямые A1K и BK, где K — середина ребра B1C1;
4)через точки A1, D и центр грани DCC1D1;
5)через точку A и центры граней АВВ1А1 и ADD1A1.
133.ПостройтесечениеправильноготетраэдраSABC плоскостью, проходящей через:
1°) середины ребер AB, BC и SB;
2°) середины ребер AB, BC и центр грани SBC;
3)середину ребра BC и центры граней SBC, SAB;
4)центры граней SBC, SAB, SAC.
Упражнения для повторения
134. |
Дан параллелограмм АВСD, точки М, N, Р, Q — середины |
||
|
соответственно сторон АВ, |
ВС, СD, DА. |
|
|
1) |
Установите взаимное расположение прямых: |
|
|
а) |
МN и PQ; б) МР и ВС; |
в) АВ и РQ; г) МQ и ВD. |
|
2) |
Установите вид четырехугольника МNРQ. |
|
|
3) |
Найдите его периметр и площадь, если длины диагона- |
|
|
лей параллелограмма АВСD равны |
||
|
6 см и 8 см, а угол между ними 60°. |
||
135. |
По данным на рис. 141 определите, |
||
|
параллельны ли прямые АВ и ЕF. |
||
Основные понятия и аксиомы стереометрии |
147 |
Итог
Аксиомы стереометрии
С1. Если прямая проходит через две точки данной плоскости, то она полностью лежит в этой плоскости.
C2. Через три точки, не лежащие на одной прямой, проходит одна и только одна плоскость.
С3. Еслидверазличные плоскости имеют общую точку, то их пересечением является прямая, проходящая через эту точку.
C4. Через две произвольные точки пространства можно провести одну и только одну прямую.
А α, B α AB α
А, В, С не лежат на одной прямой
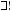 α: A α, B α, C α
α: A α, B α, C α
А α∩β α∩β = b, А b
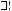 l: A l, B l
l: A l, B l
Основные утверждения
Теорема о плоскос- |
Через прямую и точку, |
|
ти, проходящей че- |
не лежащую на |
этой |
рез прямую и точ- |
прямой, проходит плос- |
|
ку |
кость и притом |
лишь |
|
одна. |
A a α: a α, A α |
Теорема о плоскос- |
Через две пересекаю- |
ти, проходящей |
щиеся прямые прохо- |
через две пересека- |
дит плоскость и при- |
ющиеся прямые |
том только одна. |
a ∩ b = {О}
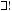 α: a α, b α
α: a α, b α
