
- •Обращение к читателю
- •Введение
- •РАЗДЕЛ 1. Функции, их свойства и графики
- •§1. Числовые множества
- •§2. Вычисления и расчёты
- •§3. Функциональные зависимости
- •§4. Основные свойства функций
- •§5. Корни n-ой степени
- •§6. Степенные функции с рациональными показателями
- •§7. Основные понятия и аксиомы стереометрии
- •§8. Взаимное расположение двух прямых в пространстве
- •§9. Параллельное проектирование
- •§10. Изображение фигур в стереометрии
- •§11. Параллельность прямых и плоскостей
- •§12. Параллельность плоскостей
- •§13. Тригонометрические функции числового аргумента
- •§14. Основные соотношения между тригонометрическими функциями
- •§15. Свойства и графики тригонометрических функций
- •§16. Тригонометрические формулы сложения и следствия из них
- •§17. Простейшие тригонометрические уравнения и неравенства
- •§18. Перпендикулярность прямой и плоскости
- •§19. Связь между параллельностью и перпендикулярностью прямых и плоскостей
- •§20. Перпендикулярность плоскостей
- •§21. Ортогональное проектирование
- •§23. Измерение расстояний в пространстве
- •§24. Измерение углов в пространстве
- •Ответы и указания к задачам
- •Предметный указатель
- •Содержание
§4. основные свойства функций
Èзучение реальных процессов часто сводится к исследованию функциональных зависимостей, описывающих эти процессы. Èсследовать функциональную зависимость — значит выявить ее характерные особенности. Õарактерными особенностями функции являются, например, ее возрастание или убывание, ч¸тность или неч¸тность, непрерывность. Ðассмотрению этих свойств и посвящен данный параграф.
1. Убывание и возрастание функций
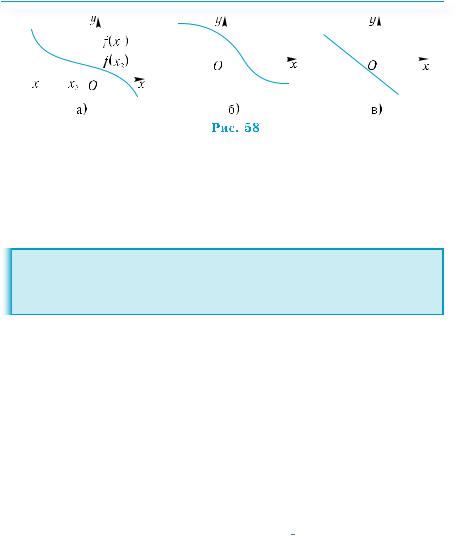
 Рассмотрим функции, графики которых изображе-
Рассмотрим функции, графики которых изображе-
ны на рис. 57.
Характернойособенностьюэтихфункцийявляется то, что большему значению аргумента соответствует большее значение функции. Такие функции называют возрастающими.
Возрастающие функции описывают процессы и явления, в которых зависимая величина увеличивается с ростом независимой. Например, температура воды при нагревании повышается с течением времени до момента кипения. Также увеличивается со временем скорость тела при свободном падении до момента падения.
Если большему значению аргумента соответствует меньшее значениефункции,тотакуюфункциюназываютубывающей(рис.58).
68 |
|
|
|
|
|
|
Функции, их свойства и графики |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
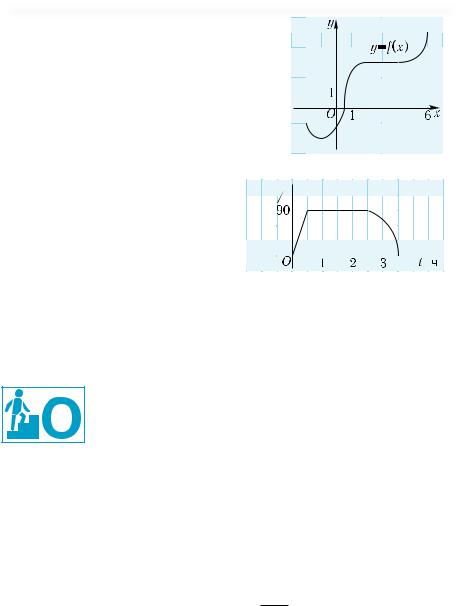
Процессы и явления, в которых зависимая величина уменьшается с ростом независимой, описываются убывающими функциями. Например, уменьшается атмосферное давление при увеличении высоты над уровнем моря, скорость тела при торможении.
Возрастающие или убывающие функции называют монотон-
ными.
Монотонный — по гречески µονοτονοζ (monotonos), от
µονοζ (monos) — один, единый и τονοζ (tonos) — напряже-
ние, ударение — однозвучный, однообразный.
Многие функции не являются монотонными. Например, квадратичная функция у = х2 (см. рис. 23) или обратная пропорциональность (см. рис. 28, 29). Однако, если рассматривать функцию у = х2 только на промежутке (– ∞; 0], то она убывает. На промежутке [0; + ∞) эта функция возрастает.
Функция у = f(х) называется возрастающей на некотором промежутке, если для произвольных точек этого промежутка х1 и x2, таких, что х1 < x2, справедливо неравенство f(х1)<f(х2).
Функция у = f(х) называется убывающей на некотором промежутке, если для произвольных точек этого промежутка х1 и x2, таких, что х1 < x2, справедливо неравенство f(х1)>f(х2).
При исследовнии функций очень важно уметь находить её промежутки возрастания и убывания, или, как говорят, находить её промежутки монотонности. Для функций, заданных графически, достаточно легко находить такие промежутки.
Пример 1. На рис. 59 изображен график функции у = f(x). Выяснить, является ли эта функция монотонной. Указать промежутки возрастания и убывания функции. Найти промежуток, на
Основные свойства функций |
69 |
котором функция принимает постоянное |
|
значение. |
|
Функция не является монотонной. |
|
Она убывает на промежутке [–2; –1] и воз- |
|
растает на каждом из промежутков [–1; 2] и |
|
[4; 6]. Функция сохраняет постоянное зна- |
|
чение, равное 3, на промежутке [2; 4]. |
|
Пример 2. На рис. 60 изобра- 

 жен график скорости движения
жен график скорости движения  автомобиля. Охарактеризовать его
автомобиля. Охарактеризовать его  движение.
движение. 
Первые полчаса скорость дви-  жения автомобиля росла от 0 км/ч
жения автомобиля росла от 0 км/ч  до 90 км/ч, то есть автомобиль дви-
до 90 км/ч, то есть автомобиль дви-  галсяускоренно.Втечениеследую-
галсяускоренно.Втечениеследую- 
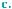
 щих двух часов (на временном промежутке [0,5; 2,5]) он двигался
щих двух часов (на временном промежутке [0,5; 2,5]) он двигался
с постоянной скоростью 90 км/ч, то есть равномерно. После этого скорость начала уменьшаться и через час автомобиль остановился. Всего он двигался 3,5 часа.
Для функций, заданных аналитически, находить промежутки возрастания и убывания достаточно трудно. Напомним решение этой задачи для уже знакомых вам функций: для линейной, квадратич-
ной и обратной пропорциональности.
У линейной функции y = kx + b коэффициент k равняется тангенсу угла наклона ее графика (прямой) к оси х. Если k > 0, то
tg ϕ > 0 и 0° < ϕ < 90°. Следовательно, угол наклона прямой к оси х
является острым, и линейная функция возрастает (см. рис. 21, а).
Если k = tgϕ < 0, то 90° < ϕ < 180°. Следовательно, угол наклона
прямой к оси х является тупым, и линейная функция убывает (см.
рис. 21, б).
Например, линейная функция y = x 2−1 возрастает, поскольку k = 12 > 0,алинейнаяфункция y = 1 −2x убывает,таккак k = −12 < 0 .
70 |
|
|
|
|
Функции, их свойства и графики |
|||||||||
|
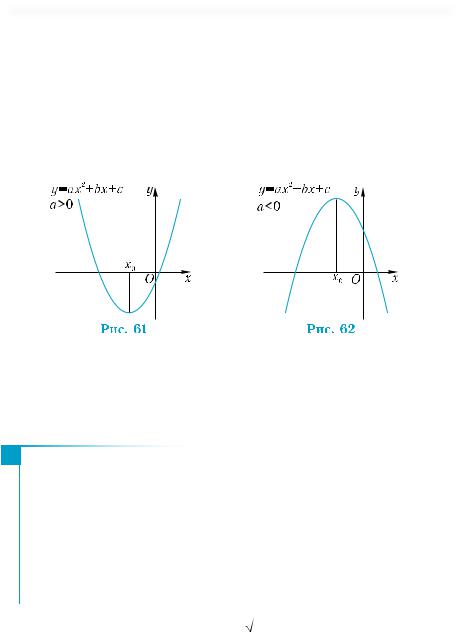
Графиком квадратичной функции у = ах2 + bх + с является пара- |
|||||||||||||
бола, |
вершина которой находится в точке с абсциссой x0 = − |
b |
. |
|||||||||||
|
||||||||||||||
Если |
|
|
|
|
|
|
|
|
|
|
|
2a |
||
а > 0, то квадратичная функция убывает на промежутке |
||||||||||||||
|
|
|
b |
|
|
|
|
|
|
b |
|
|
||
|
−∞; |
− |
|
|
и возрастает на промежутке |
|
− |
|
|
; +∞ (рис. 61). Если |
||||
|
< |
|
2a |
|
квадратичная функция |
|
|
|
2a |
|
|
|||
а |
0, то |
возрастает |
на промежутке |
|||||||||||
|
|
|
b |
|
и убывает на промежутке |
|
b |
|
|
|
(рис. 62). |
|||
|
−∞; |
− |
|
|
− |
|
|
|
; +∞ |
|||||
|
|
|
2a |
|
|
|
2a |
|
|
|
|
|
||
Например, вершина параболи у = х2 + 2х – 3 находится в точке с абсциссой x0 = − 22 = −1 и а = 1 > 0. Поэтому квадратичная функ-
ция у = х2 + 2х – 3 убывает на промежутке (−∞; −1] и возрастает на промежутке [−1; + ∞).
!Рассмотрим теперь обратную пропорциональность. Обратите внимание на то, что функция y = 1x не является убывающейвсвоейобластиопределения (−∞; 0) (0; +∞).
Сравним, например, значения этой функции в точках
х1 = –1 и х2 = 1: у(1) = 1 > y(– 1) = – 1, то есть большему зна-
чению аргумента соответствует большее значение функции. Однако, она убывает на каждом из промежутков
(−∞; 0) и (0; + ∞).
Вспомните график функции y = x и подумайте над тем, является ли она монотонной.
Основные свойства функций |
71 |
9 Контрольные вопросы
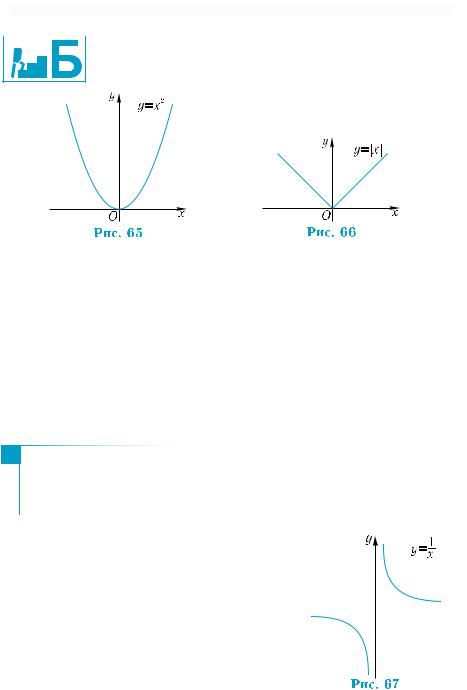
1°. Какая из функций, графики которых изображены на рис. 63, а)–г), является:
1) возрастающей; 2) убывающей?
2°. Какие из функций, графики которых изображены на рис. 63, а)–г), имеют промежутки постоянства?
3°. Какие из функций, графики которых изображены на рис. 64, а)–г), возрастают на промежутке [0; 1]?
4°. |
Какие из следующих линейных функций возрастают (убы- |
|||||||||
|
вают): |
б) у = х – 1; |
в) у = – 1; |
|
г) у = –2(х + 1)? |
|||||
|
а) у = 1 – х; |
|
||||||||
5. |
Известно, что f(– 1) = 2, f(0) = 1, f(1) = 3. Может ли функция |
|||||||||
|
у = f(х) быть монотонной? |
|
|
|
|
|||||
6°. |
Функция у = f(х) убывает на промежутке [–2; 2]. Сравните, |
|||||||||
|
если это возможно, числа f(– 0,5) и f(– 1). |
|
|
|||||||
7. |
Укажите промежуток убывания функции: |
|
||||||||
|
а) y = − |
x2 |
|
|
|
|
|
|
|
|
|
|
; |
б) у = х2 |
– 1; |
в) у = (х– 1)2. |
|||||
8°. |
3 |
|||||||||
Какая из приведенных функций возрастает на промежутке |
||||||||||
|
(0; + ∞): |
|
|
|
|
|
|
|
||
|
а) y = 3 ; |
б) y = |
1 |
; |
в) y = |
1 |
; |
г) y = − x ? |
||
|
|
−3x |
||||||||
|
x |
|
3x |
|
|
3 |
||||
72 |
Функции, их свойства и графики |
2. Четность и нечётность функций
 Рассматривая графики функций у = х2 и у = |x|
Рассматривая графики функций у = х2 и у = |x| 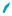
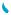 (рис. 65, 66), мы замечаем, что они симметричны относительно оси у.
(рис. 65, 66), мы замечаем, что они симметричны относительно оси у.
Функцию, график которой симметричен относительно оси у, называют чётной. Если функция у = f(x) является чётной, то ее область определения симметрична относительно начала координат, и в точках х и –х, симметричных относительно начала координат, функция принимает одно и то же значение: f(–х) = f(x). Поэтому можно дать следующее определение чётной функции.
Функция у = f(х) называется чётной, если:
1)её область определения вместе с каждой точкой х содержит и точку –х;
2)для каждого х из области определения функции выполняется равенство:
f(–х) = f(x).
!Из данного определения и предыдущих рассуждений вытекает утверждение:
функция является чётной тогда и только тогда, когда ее график симметричен относительно оси ординат.
График функции y = 1x (рис. 67) симмет-
ричен относительно начала координат. Такие функции называют нечётными. Если функция является нечётной, то ее область
определения симметрична относительно 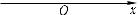 начала координат, и в точках х и –х, симметричныхотносительноначалакоординат, функция принимает противоположные зна-
начала координат, и в точках х и –х, симметричныхотносительноначалакоординат, функция принимает противоположные зна-
чения: f(– x) = – f(x).

Основные свойства функций |
73 |
Функция у = f(х) называется нечётной, если:
1)ее область определения вместе с каждой точкой х содержит и точку –х;
2)для каждого х из области определения функции выполняется равенство:
f(–х) = –f(x).
!Из данного определения и предыдущих рассуждений вытекает утверждение:
функцияявляетсянечётнойтогдаитолькотогда,когдаее график симметричен относительно начала координат.
Установление четности или нечётности функции облегчает построение графика, уменьшает объем необходимых исследований: можно исследовать поведение функции и строить ее график только для неотрицательных значений аргумента, а для отрицательных – воспользоваться упомянутой выше симметрией. В частности, если чётная функция возрастает на промежутке [a; b], a > 0, то на промежутке [–b; –a] она убывает, и наоборот.
Исследования функции на четность или нечётность проводят согласно определениям. Если хотя бы один из этих призна-
ков в обоих определениях не выполняется, то функция не является ни чётной, ни нечётной.
Пример |
3. |
|
|
Исследовать на четность и нечётность функцию: |
||||||
1) f(x) = |
x3 |
|
; |
2) f(x) = |
x4 |
; |
3) f(x) = |
x3 |
. |
|
x2 − |
3 |
x2 −3 |
x −3 |
|||||||
|
|
|
|
|
|
|||||
1) Проверим, является ли симметричной относительно нача- |
||||||||||
ла координат область определения функции. Область определе-
ния функции |
f(x) = |
x3 |
содержит все действительные числа, |
||||||||
x2 −3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
отличные от ± |
3 , то есть она симметрична относительно начала |
||||||||||
координат. Найдем |
выражение для f(–x): |
f(−x) = |
(−x)3 |
= |
|||||||
(−x)2 −3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
= − |
x3 |
. Следовательно f(х) = – f(х) и f(х) — нечётная функция. |
|||||||||
x2 −3 |
|||||||||||
|
|
|
|
|
x4 |
|
|
|
|
||
2)Область определения функции f(x) = |
|
совпадает с об- |
|||||||||
x2 −3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
ластью определения функции из предыдущего задания. Имеет

74 |
|
|
|
|
|
Функции, их свойства и графики |
||
место равенство: f(−x) = |
|
|
(−x)4 |
= |
x4 |
= f(x). Поэтому данная |
||
(−x)2 −3 |
x2 −3 |
|||||||
|
|
|
|
|||||
функция является чётной. |
|
|
|
|
||||
3) Функция f(x) = |
x3 |
|
|
не является ни чётной, ни нечётной, |
||||
x −3 |
||||||||
|
|
|
|
|
||||
поскольку ее область определения не симметрична относительно
начала координат: точка х = –3 входит в область определения, а точка х = 3 — не входит.
Для доказательства того, что функция не является ни чётной, ни нечётной, целесообразно действовать
следующим образом.
1) Проверить, симметрична ли область определения функции относительно начала координат. Если она не симметрична (см. пример 3, 3)), то функция не является ни чётной, ни нечётной. Если она симметрична, то продолжать исследование.
2) Подобрать две точки, симметричные относительно начала координат и такие, что f(– x) ≠ f(x) и f(– x) ≠ – f(x). Это и доказывает требуемое утверждение.
Пример 4. Доказать, что функция f(x) = x2 + x не является ни чётной, ни нечётной.
Её область определения симметрична относительно начала координат, но в симметричных точках 1 и –1 она принимает значения 2 и 0, которые не являются ни равными, ни противоположными числами. Поэтому не выполняется ни равенство f(–x) = = f(x), ни равенство f(– x) = – f(x) для всех х из области определения. Отсюда вытекает, что функция не является ни чётной, ни нечётной.
9 |
Контрольные вопросы |
|
|
|
|
|
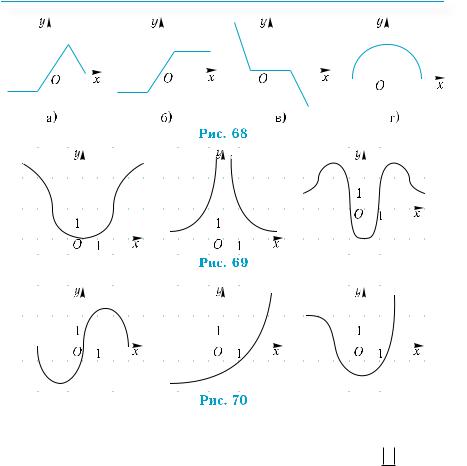
1°. |
Какая из функций, графики которых изображены на рис. 68, |
|||||
|
а) – г), может быть: 1) чётной; 2) нечётной? |
|
|
|
||
2. |
Каким свойством обладают все функции, графики которых |
|||||
|
изображены на рис. 69, и не обладает ни одна из функций, |
|||||
|
графики которых изображены на рис. 70? |
|
|
|
||
3°. |
Графики каких функций симметричны относительно оси у: |
|||||
|
а) у = 3х + 1; |
б) у = –х2; |
в) у = |
х3; |
||
|
г) y = |x|; |
д) y = 1; |
е) y = |
|
x −1 |
? |
|
|
|
||||
|
|
|
|
|
x −1 |
|
Основные свойства функций |
75 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4°. Графики каких функций симметричны относительно начала координат:
x
x?
5.Известно, что функция y = f(x) является чётной и f(2) = 1. Чему равняется f(– 2)?
6.Известно, что функция y = f(x) является нечётной и f(–3) = 2. Чему равняется f(3)?
7.Областью определения чётной функции является промежуток [а;4]. Чему равняется число а?
8.Функция y = f(x) является чётной и возрастает на промежутке [1; 2]. Возрастает ли она на промежутке [–2; –1]?
9.Может ли возрастающая функция быть: а) чётной; б) нечёт-
ной? ; =б°)а°) = 3
76 |
Функции, их свойства и графики |
3. Непрерывность и точки разрыва функций
Познакомимся еще с одним важным свойством фун- 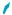
 кции—непрерывностью.Этимсвойствоммыуже
кции—непрерывностью.Этимсвойствоммыуже  неоднократно пользовались. Так, при построении графика функции мы находили несколько его точек и соединяли их линией. Аналогично действуют, когда строят график функции, пользуясь таблицей ее значений. Возникает вопрос, всегда ли можно так делать. Оказывается, что в первую очередь это зависит от того, будет ли функция непрерывной или разрывной.
неоднократно пользовались. Так, при построении графика функции мы находили несколько его точек и соединяли их линией. Аналогично действуют, когда строят график функции, пользуясь таблицей ее значений. Возникает вопрос, всегда ли можно так делать. Оказывается, что в первую очередь это зависит от того, будет ли функция непрерывной или разрывной.
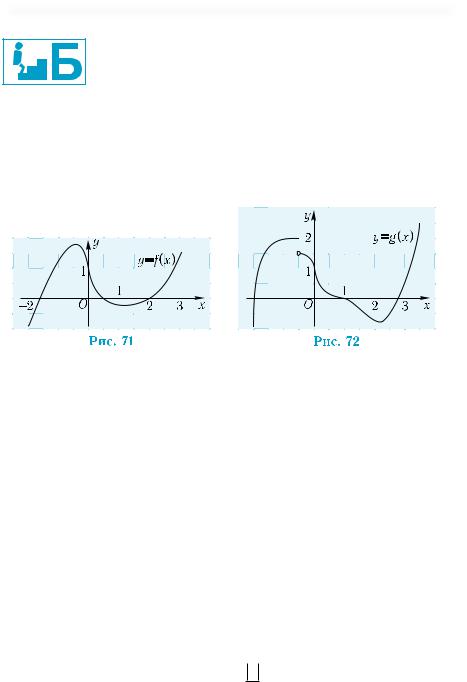
Рассмотрим графики функций у = f(x) и у = g(x), изображенные на рис. 71 и 72.
График функции у = f(x) является неразрывной линией, то есть такой, которую можно начертить, не отрывая карандаша от листа бумаги. График функции у = g(x) таким свойством не обладает. Он разорван в точке с абсциссой х = –0,5. Незаштрихованным кружочком обозначена точка, не принадлежащая графику функции у = g(x). То есть точка с координатами (–0,5; 1,5) не принадлежит этому графику. В то же время графику функции у = g(x) принадлежит точка с координатами (–0,5; 2): g(–0,5) = 2. Обратите внимание на то, что две точки с одинаковыми абсциссами не могут одновременно принадлежать графику функции у от х.
Если функция задана на некотором промежутке, и ее график на нем является неразрывной линией, то функцию называют непрерывной на этом промежутке.
Функция у = f(x) (рис. 71) непрерывна на промежутке [–2; 3]. Непрерывны в своих областях определения линейные и квадратичные функции.
О функции у = g(х) (рис. 72) говорят, что точка х = –0,5 является ее точкой разрыва. Например, точка х = 0 является точкой раз-
рыва функций y = 1x (рис. 67) и y = xx (рис. 73).
Основные свойства функций |
77 |
Непрерывная функция описывает про- |
|
цессы, происходящие плавно, без «скач- |
|
ков», то есть когда исследуемая величина |
|
за малый промежуток времени изменяет- |
|
ся мало. Именно так в обычных условиях |
|
изменяется путь, пройденный телом, ско- |
|
рость движения, температура тела при |
|
охлаждении и т.п. |
|
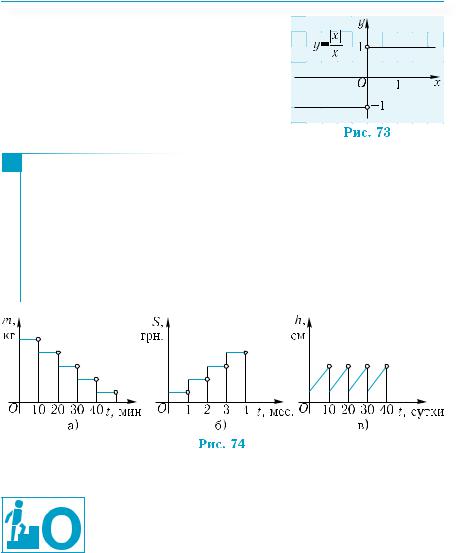
!Однакосуществуютпроцессы,вкоторыхисследуемаявеличина изменяется скачками. Например, так изменяется в зависимости от времени масса товара, который остается в машине, если его разгружают ящиками (рис. 74, а); сумма денег на банковском счете в зависимости от времени, если этот счет пополняется, но деньги с этого счета не снимаются (рис. 74, б); высота травы на газоне в зависимости от времени, если её регулярно подстригают с помощью газонокосилки (рис. 74, в), и т. п.
Важно научиться работать с подобными функциями.
Поведение функции в окрестности точек разрыва  может быть различным. Во-первых, точка разрыва может принадлежать области определения функции, а может и не принадлежать. Так, функция
может быть различным. Во-первых, точка разрыва может принадлежать области определения функции, а может и не принадлежать. Так, функция
у = g(х), график которой изображен на рис. 72, определена в точке
разрыва х1 = –1: g(–1) = 2. Функция y = |
|
x |
|
|
(см. рис. 73) не опреде- |
|||||
|
|
|||||||||
|
|
|
|
|||||||
|
|
|
|
|||||||
лена в точке х = 0. Во-вторых, функцияx |
в точке разрыва может |
|||||||||
иметь «конечный скачок», как, например, функция y = |
|
x |
|
|
(см. |
|||||
|
|
|||||||||
|
x |
|||||||||
|
|
|
|
|
|
|
|
|||
78 Функции, их свойства и графики
рис. 73), а может иметь «бесконечный скачок», как у функции y = 1x (см. рис. 67).
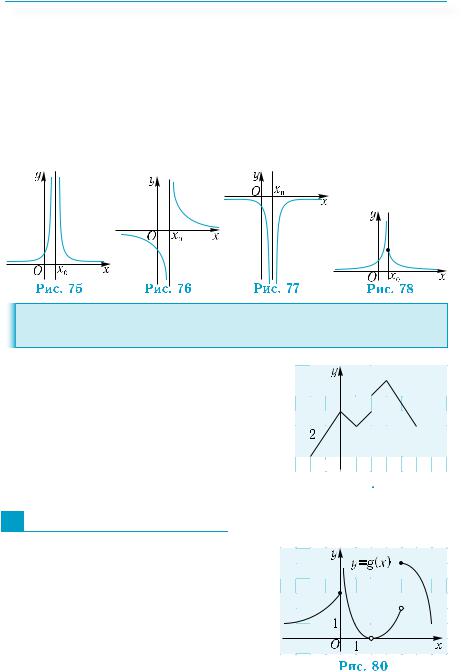
На рис. 75–78 изображены различные случаи бесконечных скачков. Мы видим, что графики функций приближаются к прямой х = х0, когда аргумент приближается к х0. Прямую х = х0 в таких случаяхназываютвертикальнойасимптотойграфика.Например,
гипербола y = 1x имеет вертикальную асимптоту х = 0.
Асимптота (по греческиασιµπτϖτος ( asymptotos)) – несовпадающая.
Рассмотрим функцию у = f(х), график
которой изображен на рис. 79. Эта фун-  кция имеет две точки разрыва: х1 = 2 и
кция имеет две точки разрыва: х1 = 2 и  х2 = 3. В точке х1 = 2 функция определена
х2 = 3. В точке х1 = 2 функция определена 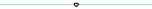
и f(2)= 3. Точка х2 = 3 является точкой раз- 
рыва функции, хотя график в этой точке  не делает скачка. В этой точке функция
не делает скачка. В этой точке функция  не определена.
не определена. 
9 Контрольные вопросы |
|
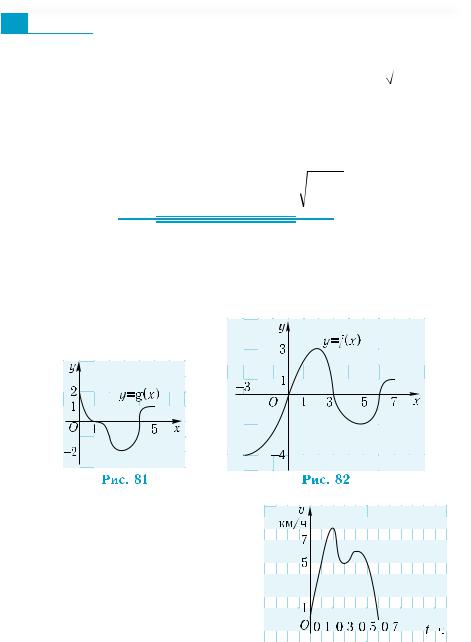
На рис. 80 изображен график фун- |
|
кции у = g(х). Какие из следующих |
|
утверждений справедливы? |
|
1) Функция у = g(х) является непре- |
|
рывной. |
|
2)Функцияимееттриточкиразрыва. |
|
3) Функция не определена в точках |
|
разрыва. |
5) g(4)= 2. |
4) g(0)= 3. |
|
Основные свойства функций |
79 |
Задачи
64°.Исследуйте функцию на четность и нечётность:
1) |
y = 5x3 − x; |
2) |
y = x2 −3; |
3) |
y = |
|
x2 |
|
|
; |
|
4) |
y = x +1; |
||||||
x |
4 −1 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5) |
y = |
|
x |
|
+ x2 −4; 6) |
y = 3; |
7) |
y = |
|
x3 |
|
; |
8) |
y = |
x3 |
. |
|||
|
|
|
|
||||||||||||||||
|
|
2x2 |
−1 |
2x −1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
65. Докажите, что функция у = f(х) не является ни чётной, ни не- |
|||||||||||||||||||
чётной, если: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1) |
f(x) = x3 −3x2 + x −1; |
2) |
f(x) = |
|
|
x |
. |
|
|
|
|||||||||
|
x |
2 +1 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
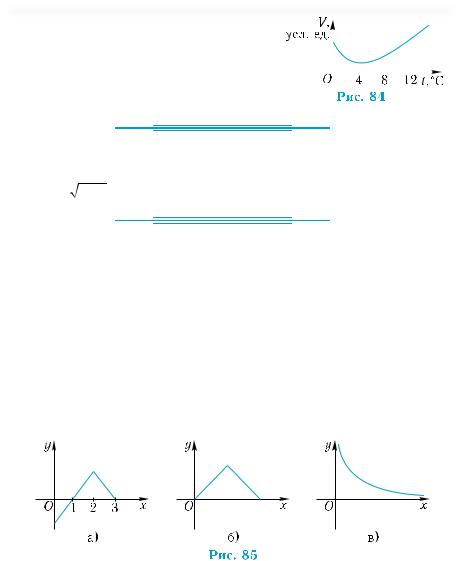
66°.На рис. 81, 82 изображены графики функций у = g(х) и у = f(х). Найдите для каждой функции:
1) область ее определения; 2) множество ее значений; 3) нули функции и промежутки знакопостоянства; 4) промежутки возрастания, убывания функции.
67°.На рис. 83 изображена зависимость скорости движения вело- 
сипедиста от времени.  1) Какой была скорость движения велосипедиста в момент времени
1) Какой была скорость движения велосипедиста в момент времени  t =18мин?
t =18мин? 
2) В какие моменты времени ско-  рость равнялась 5 км/ч?
рость равнялась 5 км/ч?  3) Укажите промежутки време-
3) Укажите промежутки време-  ни, в течение которых скорость
ни, в течение которых скорость 

 движения велосипедиста возрастала, убывала, была постоянной.
движения велосипедиста возрастала, убывала, была постоянной.
80 |
|
|
|
|
Функции, их свойства и графики |
||||||||||||
4) |
Какой была наибольшая скорость |
|
|
|
|
|
|
|
|
|
|
||||||
движения велосипедиста? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
68°.На рис. 84 изображена зависимость |
|
|
|
|
|
|
|
|
|
|
|||||||
объема воды от ее температуры. Ука- |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
жите характерные |
особенности |
этой |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||
зависимости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
69. Найдите промежутки возрастания и убывания функции: |
|||||||||||||||||
1) |
y = −x2 + 4x; |
2) y = 3x2 −6x + 4; 3) y = (x +1)(x −2); |
|||||||||||||||
4) |
y = x +1; |
5) y = |
1 |
; |
6) y = |
1 |
|
−2. |
|||||||||
x + 2 |
x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
70.Постройте график функции y = f(x), удовлетворяющей условиям:
1°) функция определена и возрастает на промежутке [–2; 2], f(–2) = –1, f(2) = 1;
2°) функция возрастает на промежутке (–∞; 2] и убывает на промежутке [2; + ∞);
3)функция чётная и убывает на промежутке [–3; 0];
4)функция определена на промежутке [–4; 4], нечётная и возрастающая.
71.На рис. 85, а)–в) изображены графики некоторых функций. Достройте каждый из них (если это возможно) до графика:
1)чётной функции; 2) нечётной функции.
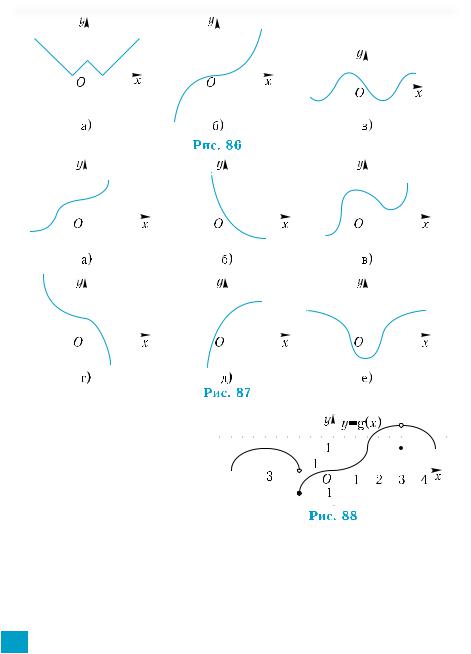
72*.Распределите графики, изображенные на рис. 86, а)–в), на 2 класса по их характерным признакам. Опишите признаки, по которым предложена классификация.
73*.Распределите все функции, графики которых изображены на рис. 87, а)–е), на 3 класса по некоторому свойству. Опишите свойства, общие для функций каждого класса.
Основные свойства функций |
81 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
74°.На рис. 88 изображен гра- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
фик функции у = g(х). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1)Являетсялиэтафункция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
непрерывной? Если нет, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
укажите ее точки разрыва. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) |
Определена ли функ- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ция в точках разрыва? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) Укажите значение фун- |
||||||||||||||||||||||||||
кции в тех точках разрыва, в которых она определена. |
||||||||||||||||||||||||||
4) |
Сколько нулей имеет функция? |
|||||||||||||||||||||||||
75. Постройте график некоторой функции, которая: |
||||||||||||||||||||||||||
1) |
в точке х = 1 имеет разрыв, но определена в этой точке; |
|||||||||||||||||||||||||
2) |
в точке х = 1 имеет разрыв и не определена в этой точке. |
|||||||||||||||||||||||||
Упражнения для повторения |
|
||
76. |
Сколько существует значений квадратного корня из числа: |
||
|
1) 36; |
2) 0; |
3) –36? |
82 |
|
|
|
|
|
Функции, их свойства и графики |
|||
77. |
Имеет ли смысл выражение: |
|
|
|
|
|
|
||
|
1) |
−49; |
2) (−7)2 ; |
|
|
3) (−7)3 ? |
|||
78. |
Вычислите: |
2) 31 11 |
|
|
|
18 |
|
||
|
1) |
(−3)2 + ( 5)2 ; |
; |
3) |
|
. |
|||
|
|
2 |
|||||||
|
|
|
3 |
5 |
|
|
|
|
|
79. |
Вынесите множитель из-под знака корня: |
|
|
||||||
|
1) |
490; |
|
2) |
12a2 ,a < 0. |
|
|
||
80. |
Упростите выражение: |
2) ( |
a − b)2 + 2 ab. |
||||||
|
1) |
48 − 300 + |
75; |
||||||
81. |
Дана функция f(x) = x + 3. |
|
|
|
|
|
|
||
1)Постройте график функции.
2)Сколько корней имеет уравнение: f(x) = 1; f(x) = –1; f(x) = x?
Итог
Основные понятия
 Геометрическая Определения интерпретация,
Геометрическая Определения интерпретация,
примеры
Функция у = f(х) называется убывающей на некотором промежутке, если для произвольныхточекэтогопромежутках1 иx2,таких,что х1 < x2, выполняется неравенство f(х1) > f(х2).
Функция у = f(х) называется возрастающей на некотором промежутке, если для произвольных точек этого промежутка х1 и x2, таких, что х1 < x2, выполняется неравенство f(х1) < f(х2).
Функция у = f(х) называется чётной, если:  1) её область определения вместе с каждой точкой х содержит и точку –х;
1) её область определения вместе с каждой точкой х содержит и точку –х;
2) для каждого х из области определения функ- 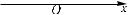 циивыполняетсяравенствоf(–x)=f(x).
циивыполняетсяравенствоf(–x)=f(x).
Функция у = f(х) называется нечётной, если:
1) её область определения вместе с каждой  точкой х содержит и точку –х; 2) для каждого х из области определения функ-
точкой х содержит и точку –х; 2) для каждого х из области определения функ-
циивыполняетсяравенствоf(–x)=–f(x).
