
- •Обращение к читателю
- •Введение
- •РАЗДЕЛ 1. Функции, их свойства и графики
- •§1. Числовые множества
- •§2. Вычисления и расчёты
- •§3. Функциональные зависимости
- •§4. Основные свойства функций
- •§5. Корни n-ой степени
- •§6. Степенные функции с рациональными показателями
- •§7. Основные понятия и аксиомы стереометрии
- •§8. Взаимное расположение двух прямых в пространстве
- •§9. Параллельное проектирование
- •§10. Изображение фигур в стереометрии
- •§11. Параллельность прямых и плоскостей
- •§12. Параллельность плоскостей
- •§13. Тригонометрические функции числового аргумента
- •§14. Основные соотношения между тригонометрическими функциями
- •§15. Свойства и графики тригонометрических функций
- •§16. Тригонометрические формулы сложения и следствия из них
- •§17. Простейшие тригонометрические уравнения и неравенства
- •§18. Перпендикулярность прямой и плоскости
- •§19. Связь между параллельностью и перпендикулярностью прямых и плоскостей
- •§20. Перпендикулярность плоскостей
- •§21. Ортогональное проектирование
- •§23. Измерение расстояний в пространстве
- •§24. Измерение углов в пространстве
- •Ответы и указания к задачам
- •Предметный указатель
- •Содержание
§5. |
корни n-ой степени |
В курсе алгебры уже рассматривалось понятие квадрат- |
|
ного корня из неотрицательного числа. В данном параграфе |
|
обобщим это понятие, определив понятие корня с произволь- |
|
ным натуральным показателем, большим 1. |
|
1. Степенные функции с натуральными показателями |
|
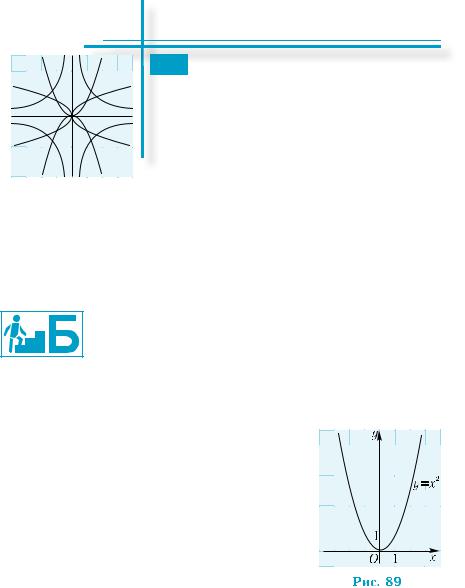
Ранее мы рассматривали функцию у = х2. Её называ- |
|
ют степенной функцией с показателем степени, рав- |
|
ным 2. Теперь мы рассмотрим степенные функции, у |
|
которых показателем степени является любое натуральное число. |
|
Степенной функцией с натуральным показателем |
|
п называют функцию вида у = хп. |
|
Рассмотрим сначала степенные функции |
|
с чётными натуральными показателями, то |
|
есть функции вида у = х2, у = х4, у = х6, ... . Все |
|
функции указанного вида обладают теми же |
|
свойствами, что и функция у = х2, график ко- |
|
торой изображен на рис. 89. Они определе- |
|
ны на множестве действительных чисел. Эти |
|
функции являются чётными. Например, для |
|
функции у = х4 имеем: у(– х) = (– х)4 = х4 = у(х). |
|
Аналогично можно обосновать чётность любой |
|
из указанных функций. Графики этих функ- |
|
ций симметричны относительно оси ординат. |
|
Степенные функции с чётными натуральными показателями |
|
неотрицательны и имеют лишь один нуль: х = 0. Поэтому их гра- |
|
фики лежат в верхней полуплоскости и проходят через начало ко- |
|
ординат. Кроме того, графики всех указанных функций проходят |
|
через точку с координатами (1; 1). |
|
84 |
Функции, их свойства и графики |
Функции у = х2, у = х4, у = х6, ... возрастают на промежутке [0; +∞) |
|
и убывают на промежутке (–∞; 0]. Их графики похожи на график, |
|
изображенный на рис. 89. |
|
Рассмотрим теперь степенные функции с |
|
нечётными натуральными показателями, от- |
|
личными от 1, то есть функции вида у = х3, |
|
у = х5, у = х7, … . Областью определения этих |
|
функций является множество действительных |
|
чисел. Они нечётны. Например, для функции |
|
у = х5 имеем: у(– х) = (– х)5 = – х5 = – |
у(х). Графи- |
ки этих функций симметричны относительно |
|
начала координат. |
|
Степенныефункцииснечётныминатураль- |
|
ными показателями возрастают. Они имеют |
|
лишь один нуль: х = 0. Их графики проходят |
|
через точку с координатами (1; 1) и похожи на |
|
график, изображенный на рис. 90. |
|
В частности, функцию у = х3 называют кубической, а ее гра- |
|
фик – кубической параболой. |
|
Пример 1. График функции f(x) = x4 + a проходит через точку
А(2; 17).
1)Найти эту функцию, то есть число а.
2)Построить ее график.
3)Сколько корней имеет уравнение f(x) = 2? f(x) = – 2?
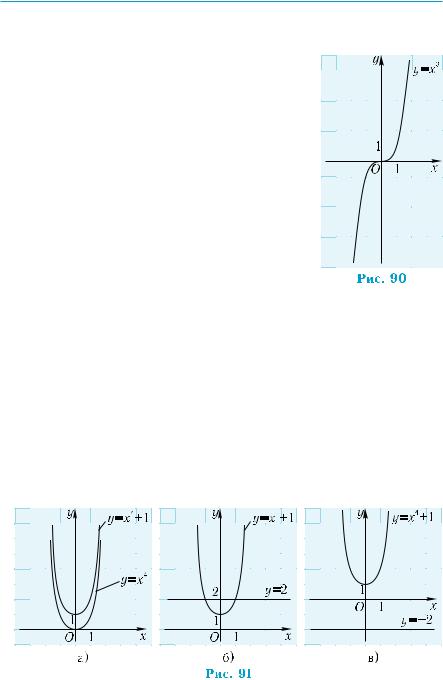
1) Поскольку график функции проходит через точку А(2; 17), то координаты этой точки удовлетворяют уравнению f(x) = x4 + a, то есть справедливо равенство 17 = 24 + а. Отсюда получаем а = 1. Итак, имеем функцию у = х4 + 1.

Корни п-ой степени |
85 |
2)График функции у = х4 + 1 можно получить из графика фун- кции у = х4 параллельным переносом его на 1 единицу в положи- тельном направлении оси ординат (рис. 91, а).
3)Необходимо установить, в скольких точках функция прини- мает значение 2. Пересечем график функции прямой у = 2. Гра- фик пересекается в двух точках (рис. 91, б). Следовательно, урав- нение х4 + 1 = 2 имеет два корня.
Уравнение х4 + 1 = –2 корней не имеет, так как график функ- ции у = х4 + 1 не пересекается с прямой у = –2 (рис. 91, в).
Многие зависимости между величинами описыва- 
 ются с помощью степенных функций с натуральны- ми показателями. Например, объем куба V являет- ся степенной функцией от длины его ребра а: V = а3;
ются с помощью степенных функций с натуральны- ми показателями. Например, объем куба V являет- ся степенной функцией от длины его ребра а: V = а3;
объем шара V является кубической функцией ее радиуса R: V (R) = 43 πR3 ; пятый член геометрической прогрессии является степенной функцией от знаменателя q: b5 = b1 q4.
!В последних двух примерах зависимость имеет вид: у = ахп, где х — аргумент, п — натуральное число, а — не- которое действительное число. Такие функции также на- зывают степенными, как и функции вида у = а(x – b)n.
Рассмотрим несколько задач на применение степенных функ- ций.
Пример 2. Вкладчик положил на свой счет в банк 1000 грн. Банк насчитывает ежегодно по схеме сложных процентов р%. Найти зависимость размера вклада от р через три года.
В соответствии с формулой сложных процентов, имеем:
|
|
|
p |
3 |
|
|
|
|
|
S3 = 1000 1 |
+ |
|
|
. |
|
|
|
||
100 |
|
|
|
||||||
|
|
|
от р является степенной функцией. |
||||||
Эта зависимость S3 |
|||||||||
|
|
|
|
|
|
|
p |
3 |
|
Ответ. S3 = |
1000 |
1 |
+ |
|
|
. |
|||
100 |
|||||||||
|
|
|
|
|
|
|
|||

86 |
Функции, их свойства и графики |
Пример |
3. Сколько корней имеет уравне- |
ние х5 + х – 1 = 0? |
|
Переписав уравнение в виде х5 =1 – х, |
|
решим задачу графическим методом. В одной |
|
системе координат построим графики функ- |
|
ций у = х5 |
и у =1 – х. Корни уравнения — это |
абсциссы общих точек графиков функций. |
|
Графики пересекается в одной точке (рис. 92). |
|
Следовательно, уравнение имеет один ко- |
|
рень. |
Один. |
Ответ. |
|
99 Контрольные вопросы |
|
1°. |
Пересекает ли график функции у = х6 прямая: а) х = 0; б) у = –1? |
|||||||||||||||||||||
2°. |
Пересекает ли график функции у = |
х5 |
прямая: |
д) у = –1? |
|
|||||||||||||||||
|
|
а) х = 0; |
|
б) |
х = 100; |
в) |
х = –1000; |
г) у = 10; |
|
|||||||||||||
3. |
Какие свойства функций у |
= |
х4 и у = х5 является общими? |
|
|
|||||||||||||||||
4. |
Сколько корней имеет уравнение: |
= –7; |
|
|
г) х11 = 11? |
|
|
|||||||||||||||
|
|
а) х4 |
= 2; |
|
|
|
б) х2 |
= –3; |
|
в) х5 |
|
|
|
|
||||||||
5. |
Даны функции f(x) = x5 |
и g(x) = x10. Что больше: нуль или число: |
||||||||||||||||||||
|
|
а) f(–5) f(–7); |
|
|
б) f(–10) – f(–20); |
|
в) g(–10) – g(–20)? |
|
||||||||||||||
6. |
Сравните числа: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
5 |
|
7 |
|
4 |
7 |
6 |
7 |
5 |
7 |
5 |
6 |
|
4 |
6 |
|
5 |
6 |
− |
4 |
6 |
|
|
а) |
|
и |
|
; |
б) |
|
и |
|
; в) |
|
и |
|
; |
г) |
|
и |
5 |
. |
||
|
|
6 |
|
|
|
5 |
|
5 |
|
4 |
|
6 |
|
|
5 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
2. Понятие корня n-ой степени |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
Как известно, квадратным корнем из числа а назы- |
||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
вают число, квадрат которого равняется |
а. Анало- |
|||||||||||||||
|
|
|
|
|
|
гично определяется понятие корня |
п-ой степени из |
|||||||||||||||
|
числа а, где |
п – произвольное натуральное число, большее 1. Это |
||||||||||||||||||||
понятие необходимо для решения многих задач, сводящихся к на- хождению корней уравнения хп = а. Например, нахождение ребра куба х по его объему V сводится к решению уравнения х3 = V.
Корнем п-ой степени (п N, п > 1) из числа а называ-
ется число, п-ая степень которого равна а.
Так, корнем четвертой степени из числа 256 является число 4, а также –4, так как 44 = (–4)4 = 256; корень пятой степени из числа 243 равен числу 3, поскольку 35 = 243. Число 5 является корнем

Корни п-ой степени |
87 |
третьей степени из числа 125, ибо 53 = 125, и корнем четвертой степени из числа 625, так как 54 = 625. Корень третьей степени называют еще кубическим корнем. По-видимому, это связано с тем, что объем V куба по его ребру х вычисляется по формуле V = х3. Длина ребра куба является кубическим корнем из его объ- ема.
Операцию нахождения корня п-ой степени из числа а называ-
ют извлечением корня п-ой степени из числа а. Корень п-ой степени определен лишь для натуральных п ≥ 2.
!Понятно, что корня чётной степени из отрицательного числанесуществует,таккакчётнаястепеньлюбогодейс- твительного числа является неотрицательным числом.
Рассмотрим функцию у = х3. Произвольная |
|
прямая у = а пересекает график этой функции |
|
в единственной точке (рис. 93). А это означает, |
|
что для любого числа а существует единствен- |
|
ное значение х, третья степень которого равна |
|
а. Иначе говоря, для любого действительного |
|
числа а существует единственное значение |
|
корня третьей степени из этого числа. |
|
Аналогично можно прийти к общему выво- |
|
ду. Для произвольного действительного числа |
|
а и любого нечетного натурального числа п су- |
|
ществует единственное значение х, п-ая сте- |
|
пень которого равна а. Это значение является |
|
корнем п-ой степени из числа а. При нечётном |
|
п его обозначают через n a (читают: корень |
|
п-ой степени из числа а). |
|
Например, запись 3 −27 означает кубический корень из числа |
|
–27. Из определения корня вытекает, что 3 −27 = –3, так как (–3)3 = |
|
= –27. Запись 5 0,03125 означает корень пятой степени из числа |
|
0,03125. Его значение равно 0,5, поскольку (0,5)5 |
= 0,5 · 0,5 · 0,5 × |
× 0,5 · 0,5 = 0,03125. |
имеет место ра- |
По определению, для произвольного числа а |
|
венство: |
|
(2k+1 a)2k+1 = a. |
|
Заметим, что при произвольном натуральном значении k чис- |
|
ло 2k + 1 нечётно. |
|

88 |
Функции, их свойства и графики |
Рассмотрим теперь функцию у = х4. Про- |
|
извольная прямая у = |
а при а > 0 пересе- |
кает график этой функции в двух точках |
|
(рис. 94), то есть для любого положительно- |
|
го числа а существуют два значения х, чет- |
|
вертая степень которых равняется а. Иначе |
|
говоря, для любого положительного числа а |
|
существуют два значения корня четвертой |
|
степени из этого числа. |
|
Аналогично можно придти к общему выводу. Для произволь- |
|
ного а > 0 и чётного натурального числа п существуют два проти- |
|
воположных числа, п-ая степень которых равна а. При а = 0 такое |
|
число единственное, х = 0. При а < 0 таких чисел не существует. |
|
При чётном п знаком n a обозначают неотрицательный корень п-ой степени из числа а. Отрицательный корень п-ой степени из
положительного числа а записывается так: −n a.
По определению, для произвольного неотрицательного числа а имеет место равенство:
(2k a)2k = a.
Например, запись 6 729 означает неотрицательный корень
шестой степени из 729. Имеем: 6 729 = 3, ибо число 3 является неотрицательным и 36 = 729.
Пример 4. Вычислить: |
( |
22)2 + (3 −2)3 |
. |
|
|||||||
|
|
2 |
5 32 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
|
Согласно |
определению |
корня п-ой степени, имеем: |
||||||||
( 22)2 + (3 −2)3 |
22− 2 |
= |
20 |
= 5. |
|
|
|||||
2 |
5 32 |
= |
2 2 |
4 |
|
|
|||||
|
|
|
|
|
|
|
|
||||
Ответ: 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Как известно, |
для квадратного корня знаком |
a |
|||||||
|
|
||||||||||
|
|
обозначается неотрицательный корень из неотри- |
|||||||||
|
|
цательного числа |
а. |
|
|
||||||
Поэтому a2 = a : ведь число |а| неотрицательно и его квадрат равен а2. Точно так же при произвольном чётном

Корни п-ой степени |
89 |
показателе корня, равном 2k, знаком 2k a мы обозначили неотри- цательный корень 2k-ой степени из числа а. Поэтому
2k a2k = a .
Действительно, число |а| неотрицательно и его 2k-ая степень равна а2k.
В этой формуле нельзя опускать знак модуля, иначе для отрица- тельных значений а получим неправильные результаты. Так,
4 (−1)4 = 4 1 =1 . Если же воспользоваться указанной формулой и
опустить знак модуля, получим ошибочный результат 4 (−1)4 = −1.
Рассмотрим теперь корни нечётной степени. При нечётном п = 2k + 1 единственное значение корня из произвольного числа а
мы обозначали |
через |
2k+1 a . Согласно определению, 3 53 = 5, |
3 (−5)3 = −5, 3 a3 |
= a, 5 a5 |
= a и т.д. для произвольного числа а. Та- |
ким образом, для корней нечётной степени справедлива формула:
|
|
|
|
|
|
|
2k+1 a2k+1 = a . |
|
|
|
|
|
|
Например, |
3 ( |
3 − 2)3 = 3 − 2, но 4 ( 3 − 2)4 = |
|
3 − 2 |
|
= 2− 3 , |
|||||||
|
|
||||||||||||
так как |
3 < 2. |
|
|
|
|
|
|
|
|
||||
Пример |
5. |
|
|
Упростить выражение 6 x6 |
+ 5 x5 . |
||||||||
Согласно |
приведенным |
выше |
формулам, имеем: |
||||||||||
6 x6 + 5 x5 |
= |
|
x |
|
+ x . Если х ≥ 0, то |x| = x и |x| + x = x + x = 2x. Если же |
||||||||
|
|
||||||||||||
х < 0, то |x| = |
|
– |
|
x и |x| + x = – x + x = 0. |
|
|
|
|
|
||||
Ответ: 2х, если х ≥ 0; 0, если х |
< 0. |
|
|
|
|
|
|||||||
Пример 6. |
Построить график функции y = 4 (x − 2)4 . |
Так как 4 (x − 2)4 = x − 2 , то имеем фун- |
|
кцию y = |x – 2|, график которой можно полу- |
|
чить из графика функции у = |х| параллель- |
|
ным переносом последнего на 2 единицы в |
|
положительном направлении оси абсцисс |
|
(рис. 95). |
|

90 Функции, их свойства и графики
99 Контрольные вопросы
1°. Верно ли, что число –3 является корнем четвертой степени из числа 81?
2°. Верно ли, что корень четвертой степени из числа 81 равен
–3?
3°. Сколько существует корней пятой степени из числа –1024? 4°. Сколько существует корней четвертой степени из числа 625? 5°. Какие из данных выражений не имеют смысла:
−16; 3 −27; 6 (−2)2 ; 6 (−2)3 ; 5 (−2)3 (−3)2 ; 4 (−2)3 (−3)2 ?
6.Известно, что объем V шара вычисляется по формуле V = 43 πR3 , где R — радиус шара. Кубическим корнем из какого числа является радиус шара, если V = 92 ?
7.Чему равняется: а) 4 74 ; б) 6 (−7)6 ; в) 5 (−7)5 ?
8*. Между какими двумя последовательными целыми числами находится число 3 15?
3. Арифметический корень п-ой степени и его свойства
 Раньше отмечалось, что если п — нечетное число,
Раньше отмечалось, что если п — нечетное число,
то выражение n a имеет смысл при любом значе-
нии а; если п — чётное число, то выражение n a имеет смысл лишь при а ≥ 0 и принимает только неотрицательное значение.
Выражение n a при а ≥ 0 имеет смысл как при чётном п, так и при нечётном п, и его значение неотрицательно. Его называют арифметическимкорнемп-ойстепениизчислаа.Числоаназы-
вается подкоренным выражением, п — показателем корня.
Арифметическим корнем п-ой степени из неотрица- тельного числа а называют неотрицательное чис- ло, п-ая степень которого равняется а.
Корень нечётной степени из отрицательного числа можно вы- разить через арифметический корень. Например 3 −18 = −3 18 , так
как, согласно определению, |
3 − |
1 |
= − |
1 |
, − 3 |
1 |
= − |
1 |
. Вообще, при |
|
|
8 |
|
2 |
|
8 |
|
2 |
|

Корни п-ой степени |
91 |
произвольном положительном а и при нечётном п справедливо
равенство n −a = −n a.
Нам уже известны свойства арифметического квадратного кор- ня. Аналогичные свойства имеет арифметический корень п-ой степени и при п > 2.
Свойство 1. Если а ≥ 0 и b ≥ 0, то n ab = n a n b.
Арифметический корень п-ой степени из произведе- ниядвухнеотрицательныхчиселравенпроизведению арифметических корней п-ой степени из этих чисел.
Свойство 2. Если а ≥ 0 и b > 0, то n ab = nn ab .
Арифметический корень п-ой степени из дроби, чис- литель которой неотрицателен, а знаменатель поло- жителен,равенарифметическомукорнюп-ойстепени из числителя, делённому на арифметический корень п-ой степени из знаменателя.
Приклад 7. Вычислить:
1) 6 64 729; 2) 5 8 5 4; |
3) |
4 3 |
13 |
; |
4) |
4 243 |
. |
|
81 |
4 3 |
|||||||
|
|
|
|
|
|
1) Согласно свойству 1, 6 64 729 = 6 64 6 729 = 2 3 = 6.
2) Применяя свойство 1, будем иметь: 5 8 5 4 = 5 8 4 = 5 32 = 2. 3) Применяя свойство 2, получим: 4 31381 = 4 25681 = 4425681 =
=43 =113.
4)Применяясвойство2,будемиметь: 4 42433 = 4 2433 = 4 81 = 3.
Ответ. 1) 6; 2) 2; 3) 113 ; 4) 3.
Пример 8. Сравнить значения выражений 3 729 и 6 729. Применяяопределениекорня,последовательнобудемиметь:
3 729 = 9 = 3, 6 729 = 6 36 = 3.

92 Функции, их свойства и графики
Мы видим, |
что значения этих выражений равны друг другу, то |
|
есть 3 729 |
= |
6 729. |
Ответ: |
3 729 = 6 729. |
|
Анализируя последний пример, можно предположить справед- ливость следующих утверждений.
Свойство 3. Если а ≥ 0, то для натуральных п и k, больших 1, справедливо равенство n k a = nk a.
Свойство 4. Если а ≥ 0, то для натуральных п, m и k, п > 1, справедливо равенство nk amk = n am .
Свойство 4 иногда называют основным свойством корня. Его можно сформулировать так:
еслипоказателькорняипоказательстепениподкоренно- го выражения умножить или разделить на одно и то же натуральноечисло,тозначениекорнянеизменится.
Например, 8 34 = 3; 8 36 = 4 33 .
Свойства 1 – 2 доказываются аналогично свойствам арифмети-
ческого квадратного корня. Эти же идеи можно использовать для доказательства свойств 3 – 4.
Свойства 1 — 4 позволяют вносить множитель под знак ариф-
метического корня и выносить множитель из-под знака корня.
Например, разлагая подкоренное выражение числа 4 48 на
простые множители и применяя определение корня и свойство 1, |
|||||||
можно |
|
вынести |
множитель |
из-под |
знака |
корня: |
|
4 48 = 4 |
24 |
3 = 4 24 |
4 3 = 24 |
3. Выполняя эти преобразования в об- |
|||
ратном |
порядке, |
можно |
внести |
множитель |
под знак |
корня: |
|
23 3 = 3 23 3 3 = 3 23 3 = 3 24. |
|
|
|
||||
Пример |
9. Упростить выражение: |
|
|
||||
1) 3 54 + 4 48 −33 2 −34 3; 2) 27 4 9; 3) 4 33 3.
1)Выносямножителииз-подпервыхдвухкорней,будемиметь:
3 54 + 4 48 −33 2 −34 3 = 3 27 2 + 4 16 3 −33 2 −34 3 = = 3 27 3 2 + 4 16 4 3 −33 2 −34 3 = 33 2 + 24 3 −33 2 −34 3 = −4 3.

Корни п-ой степени |
93 |
2) Воспользовавшись основным свойством корня и свойством 1,
получим: 27 4 9 = 27 4 32 = 27 3 = 27 3 = 81 = 9.
3) Внесем множитель 3 под знак арифметического корня третьей
степени: 4 33 3 = 4 3 33 3 3 = 4 3 34 . Согласносвойству3, 4 3 34 |
= 12 34 . |
Применяя основное свойство корня, получим: 12 34 = 3 3. |
Итак, |
4 33 3 = 3 3. |
|
Ответ. 1) −4 3; 2) 9; 3) 3 3 . |
|
Если необходимо перемножить или разделить корни из по- ложительных чисел с одинаковыми показателями, то, согласно свойствам 1 и 2, достаточно перемножить или разделить их под- коренные выражения и записать произведение или частное под знаком корня с тем же показателем.
! Если же показатели корней, которые перемножаются или делятся, различны, то необходимо их привести к общему показателю. Это делается на основании основ- ного свойства корня, то есть каждый показатель корня умножается на подобранный дополнительный множи- тель одновременно с возведением подкоренного выра- жения в ту же степень. За общий показатель следует взять наименьшее общее кратное показателей корней, которые перемножаются или делятся.
Пример 10. Представить выражение в виде корня из некоторо-
го числа: 1) 3 2 4 5; 2) 36 39 .
1) Поскольку множители являются корнями различных сте- пеней, то приведем их к общему показателю. Наименьшее общее кратное показателей 3 и 4 равно 12. Показатели корней следует умножить на дополнительные множители: 12 : 3 = 4, 12 : 4 = 3. Согласно основному свойству корня, имеем:
3 2 4 5 = 3 4 24 4 3 53 = 12 24 12 53 .
Используя свойство 1, перемножим полученные корни с одина-
ковыми показателями: 12 24 12 53 = 12 24 53 = 12 2000 .
2) Учитывая, что наименьшее общее кратное показателей кор- ней, то есть чисел 3 и 6, равно 6, то, согласно основному свойству корня, будем иметь:
94 |
|
|
|
|
|
Функции, их свойства и графики |
|
3 9 |
= |
6 92 |
= 6 92 = 6 |
27 = 6 33 = 3. |
|
6 3 |
6 3 |
|
||||
|
|
3 |
|
|||
Ответ. 1) |
12 2000 ; 2) |
3 . |
||||
|
|
|
|
|
Использовать свойства 1–4 при преобразовании вы- |
|
|
|
|
|
|
||
|
|
|
|
|
ражений с корнями следует очень осторожно, обя- |
|
|
|
|
|
|
зательно проверяя выполнение условий, при кото- |
|
|
|
|
|
|
рых они справедливы. В противном случае можно |
|
|
|
|
|
|
||
получить неправильный результат. Например, 4 a2 = a лишь
при а ≥ 0. При отрицательных значениях а это равенство неверно.
Чтобы убедиться в этом, подставьте, например, а = –1 и посмотри- те, какой вид примет правая часть равенства.
Если а < 0, то для применения свойства 4 необходимо сначала преобразовать корень: 4 a2 = 4 (−a)2 . Поскольку –а > 0, то к послед
нему корню можно применить свойство 4: 4 a2 = 4 (−a)2 = −a.
Пример 11. Вынести множитель из-под знака арифметическо-
го корня: 1) 4 6a13b6 (a > 0,b > 0); 2) 4 6a13b6 (a > 0,b < 0).
1) 4 6a13b6 = 4 6a12 a b4 b2 = 4 a12 4 b4 4 6ab2 = a 3 b 4 6ab2 =
= a3b4 6ab2 , так как a > 0,b > 0.
2) 4 6a13b6 = 4 a12 4 b4 4 6ab2 |
= |
|
a |
|
3 |
|
b |
|
4 6ab2 = −a3b4 6ab2 , посколь |
|||||
|
|
|
|
|||||||||||
ку a > 0,b < 0. |
2) −a3b4 6ab2 . |
|||||||||||||
Ответ. 1) a3b4 6ab2 ; |
||||||||||||||
Пример 12. В выражении |
b4 a |
|
внести множитель под знак |
|||||||||||
корня, если b < 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку b < 0 |
и |
|
b |
|
= 4 b4 , |
|
то −b = 4 b4 . Таким образом, |
|||||||
|
|
|
||||||||||||
b4 a = −4 b4 4 a = −4 b4a , согласно свойству 2.
Ответ. −4 b4a .

Корни п-ой степени |
95 |
99 |
Контрольные вопросы |
|
|
|
1°. |
Какие из следующих чисел являются арифметическими кор- |
|||
|
нями соответствующей степени: |
|
||
|
а) 3 −25; |
б) 5 25; |
в) 4 23; |
г) 4 (−7)2 ? |
2°. |
Как записать корень п-ой степени из отрицательного числа |
|||
|
через арифметический корень той же степени: |
|||
|
а) 3 −15; |
б) 5 −37; |
в) 7 −23; |
г) 9 −7 ? |
3.Чему равно значение выражения:
а°) ( 3 −15)3 ; |
б°) 4 74 ; |
в) 5 (−37)5 ; |
г) 10 (−5)10 ? |
|
||||||
4°. Чему равно значение выражения: |
|
|
|
|
|
|||||
а) 3 8 27 125; |
б) 3 1000 |
1 |
64; |
в) 4 |
16 81 10000; |
|||||
27 |
||||||||||
г) 3 27; |
д) 3 1000 ; |
|
81 |
|
|
81 |
|
|
||
е) |
4 |
; |
ё) 4 |
|
? |
|||||
|
0,0256 |
|
||||||||
64 |
216 |
|
625 |
|
|
|
|
|||
5°. К какому общему показателю следует привести корни при ум- ножении или делении:
а) 3 2 и 6 3; б) 3 2 и 4 3; в) 4 2 и 6 3; г) 10 2 и 15 3 ?
6.При каких значениях букв, входящих в выражение, справед- ливо равенство:
а) |
4 |
a4 = a ; |
б) |
4 |
a4 |
= −a ; в) 3 a3 |
= a ; г) |
ab = −a −b ? |
7*. Верно ли равенство: |
|
|
|
|||||
а) |
|
a3b = a ab; |
|
|
б) 3 a4b = a3 ab; |
в) |
a3b2 = ab a ? |
|
Задачи
82°.Укажите |
промежутки, на которых возрастает и на которых |
|||||||
убывает функция: |
2) |
|
3) |
|
||||
1) |
y = x3 ; |
y = x4; |
y = −x3 ; |
|||||
4) |
y = −x4; |
5) |
y = (1 − x)6 ; |
6) |
y = (x + 2)5 . |
|||
83. Исследуйте на четность и нечётность функцию: |
||||||||
1°) |
y = x4 + 2; |
|
2°) |
y = −x5 + 2x3 − x; |
||||
3°) |
y = |
4x5 |
; |
|
4) |
y = x3 + x2 + x +1. |
||
|
|
|||||||
|
|
x −1 |
|
|
|
|
||

96 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функции, их свойства и графики |
|||||||||||||
84. |
Постройте график функции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1°) |
y = (x −2)3 ; |
|
|
|
|
2°) y = x3 −2; |
3) |
y = (x −3)4 + 2 . |
|||||||||||||||||||||
85. |
Сколько корней имеет уравнение: |
1 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
1°) x3 = 3 − x ; |
2°) |
|
|
x = x4 ; |
3°) x5 +1 = |
; |
|
4) |
х3 = |x|? |
||||||||||||||||||||
86. |
Решите уравнение: |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|||||||||||
= –64; |
|
3) х4 = 625; |
|
|
|
|
4) |
х4 = –625. |
||||||||||||||||||||||
|
1) х3 = 64; |
|
|
2) |
х3 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
87°.Найдите значение выражения: |
|
91 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1) 3 2 3 500 ; |
2) |
4 324 4 4 ; |
3) |
3 −1 |
|
; |
|
|
|
4) |
3 36 49 ; |
||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
125 |
|
|
|
|
|
|
|
|
|
|
|
||
|
5) |
5 |
710 |
|
; |
|
|
6) |
3 0,027 36 ; 7) 4 48 27 ; |
|
|
8) |
5 162 48 . |
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
88°.Представьте выражение в виде дроби: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
1) |
3 |
8 |
; |
2) |
3 64; |
3) |
4 |
5 |
; |
4) 4 625 |
|
; |
5) |
5 |
6 |
. |
|
||||||||||||
|
|
81 |
|
|
||||||||||||||||||||||||||
|
|
27 |
|
|
|
|
15 |
|
|
|
|
|
256 |
|
|
|
|
a5 |
||||||||||||
89°.Вычислите: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 48 : 3 3 . |
|
||||||||||
|
1) |
3 243 : 3 9; |
|
2) |
3 256 : 3 4; |
3) |
3 250 : 3 2; |
|
|
4) |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||
90. |
Представьте выражение в виде корня из некоторого числа: |
|||||||||||||||||||||||||||||
|
1°) 3 3 5; |
2°) 4 |
3 10 ; |
3°) 3 |
4; |
4°) 4 5 12; 5) 3 2 5; |
6) 5 43 3. |
|
||||||||||||||||||||||
91. |
Решите уравнение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1) |
4 x −0,2 = 0 ; 2) |
8 x +3 = 0 ; |
3) |
3 x −2 = 0; |
|
|
4) |
3 x +3 = 0 . |
|||||||||||||||||||||
92. |
Упростите выражение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1°) |
3 1 b3 ; |
|
|
2°) 5 243d15 |
; |
3) |
4 16a4 ,a > 0 |
;4) |
4 16 c4 ,c < 0 . |
||||||||||||||||||||
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
81 |
|
|
|
||
93. |
Сократите дробь: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
7 + 7 |
|
|
|
|
|
|
a −1 |
|
|
|
a −81b |
|
|
|
|
|
|
8a −1 |
||||||||||
|
1°) |
7 +1 |
; |
|
2°) |
|
|
|
; |
|
3) |
|
; |
4) |
|
. |
||||||||||||||
|
|
|
|
a +1 |
|
a −9 b |
||||||||||||||||||||||||
94. |
|
|
|
|
43 a2 + 23 a +1 |
|||||||||||||||||||||||||
Вынесите множитель из-под знака корня: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
1°) 3 250; |
|
|
2°) 4 405; |
|
|
3) |
3 54a7 ; |
|
|
|
|
4) |
4 32b6 ; |
||||||||||||||||
|
5) 4 5a6 ,a < 0; 6) |
3 m8n2 ; |
|
7) |
4 16a3b11 . |
|
|
|
|
|
|
|
|
|||||||||||||||||
95. |
Внесите множитель под знак корня: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
1°) −55 5 ; |
|
|
2) |
b6 2,b ≤ 0; |
3) ab4 2,a ≥ 0,b ≤ 0 ; |
4) b4 −b . |
|||||||||||||||||||||||

Корни п-ой степени |
|
|
|
|
|
|
|
97 |
|
96. |
Упростите выражение: |
|
|
|
|
|
|
||
|
1°) 2 5 −2 45 |
+ 2 20 |
; |
2°) 3 40 + 4 162 −34 2 −23 5 ; |
|
||||
|
3°) 43 6 + 3 135 |
− 3 384 |
− 3 40 ; |
4°) ( 12 + |
75 + |
27): |
15 ; |
|
|
|
5) (3 4 −33 2)(3 16 +33 8 + 93 4);6) (4 3 − 4 27 )(4 3 + 4 27); |
|
|||||||
|
7) (4 3 − 4 27)2 −4 3 ; |
|
8) (7 6 6 |
−64 216)4 . |
|
|
|
||
97. |
Найдите область определения функции: |
|
|
|
|
|
|||
|
1°) y = 4 5x −15; 2°) y = 3 x2 −1; |
3°) y = x |
2 −1; |
4) y = 5 |
|
x |
. |
||
|
|
x +1 |
|||||||
|
|
|
|
|
|
|
|
|
|
98. Поток жидкости, проходящей через поперечное сечение тру-
|
πR4 |
|
p − p |
|
бы, вычисляется по формуле: Q = |
8η |
|
1 2 |
, где Q — поток, |
|
||||
|
|
l |
||
R — радиус трубы, l — длина трубы, р1 |
– р2 — разность давле- |
|||
ний на концах трубы, η — вязкость жидкости. Выразите ради- |
||||
ус трубы R через другие переменные. |
|
|
|
|
99. Первый член геометрической прогрессии равен 2. Чему равен ее знаменатель, если:
1) седьмой ее член равен 1458;
2) произведение ее шести первых членов равно 728;
3*) произведение ее первых п членов равно Р ?
Упражнения для повторения
100. Постройте график функции:
1) y = |
3 |
; |
2) y = 3 x −2; 3) y = x5 + 2; |
4*) y = |
x −1 |
. |
|
x + 2 |
|
|
|
x −1 |
|
101.Найдите множества значений функций, заданных в задаче
100.
102.В каких точках графики функций, заданных в задаче 100, пересекают оси координат?

98 |
|
|
|
|
|
|
Функции, их свойства и графики |
|||
|
|
|
|
Итог |
|
|
|
|
||
|
Основные понятия |
|
|
|||||||
|
|
|
|
|
||||||
Определение |
|
Примеры |
Применение |
|||||||
Корнем п-ой степени |
3 |
−27 = −3 . |
|
Операция извлечения |
|
|||||
(n Ν, n > 1) из числа а |
Корень четвер- |
корня п-ой степени яв- |
|
|||||||
называется число, |
п-ая |
той степени из |
ляется |
обратной для |
|
|||||
степень которого равня- |
числа |
81 |
рав- |
операции возведения |
|
|||||
ется а. |
|
няется |
3 |
или |
в п-ую степень. |
|
||||
|
|
–3. |
|
|
|
|
|
|
|
|
Арифметическим |
кор- |
|
1 |
|
1 |
, 4 81 = 3. |
Понятие арифметичес- |
|
||
нем п-ой степени из не- |
3 |
8 |
= |
2 |
кого корня приводит к |
|
||||
отрицательного числа а |
|
|
|
|
однозначности нахож- |
|
||||
называют неотрицатель- |
|
|
|
|
|
|
дения |
неотрицатель- |
|
|
ное число, п-ая степень |
|
|
|
|
|
|
ного корня из неотри- |
|
||
которого равняется |
а. |
|
|
|
|
|
|
цательного числа. |
|
|
Основные утверждения
|
|
|||||
Арифметический корень п-ой степени из про- |
n ab = n a n b, |
|||||
изведения двух неотрицательных чисел равен |
a ≥ 0,b ≥ 0. |
|||||
произведению арифметических корней п-ой |
||||||
степени из этих чисел. |
|
|
|
|
|
|
Арифметический корень п-ой степени из дроби, |
|
a |
|
n a |
, |
|
числитель которой неотрицателен, а знамена- |
n |
b |
= |
|
||
n b |
||||||
тель положителен, равен арифметическому |
|
|
|
|||
корню п-ой степени из числителя, деленному |
a ≥ 0,b > 0. |
|||||
на арифметический корень п-ой степени из |
|
|
|
|
|
|
знаменателя. |
|
|
|
|
|
|
Если показатель корня и показатель степени |
n k a = nk a, |
|||||
подкоренного выражения умножить или раз- |
||||||
nk amk |
= n am . |
|||||
делить на одно и то же натуральное число, то |
||||||
значение корня не изменится. |
|
|
|
|
|
|
