
- •Обращение к читателю
- •Введение
- •РАЗДЕЛ 1. Функции, их свойства и графики
- •§1. Числовые множества
- •§2. Вычисления и расчёты
- •§3. Функциональные зависимости
- •§4. Основные свойства функций
- •§5. Корни n-ой степени
- •§6. Степенные функции с рациональными показателями
- •§7. Основные понятия и аксиомы стереометрии
- •§8. Взаимное расположение двух прямых в пространстве
- •§9. Параллельное проектирование
- •§10. Изображение фигур в стереометрии
- •§11. Параллельность прямых и плоскостей
- •§12. Параллельность плоскостей
- •§13. Тригонометрические функции числового аргумента
- •§14. Основные соотношения между тригонометрическими функциями
- •§15. Свойства и графики тригонометрических функций
- •§16. Тригонометрические формулы сложения и следствия из них
- •§17. Простейшие тригонометрические уравнения и неравенства
- •§18. Перпендикулярность прямой и плоскости
- •§19. Связь между параллельностью и перпендикулярностью прямых и плоскостей
- •§20. Перпендикулярность плоскостей
- •§21. Ортогональное проектирование
- •§23. Измерение расстояний в пространстве
- •§24. Измерение углов в пространстве
- •Ответы и указания к задачам
- •Предметный указатель
- •Содержание

§23. измерение расстояний в пространстве
В этом параграфе рассматривается измерение расстояний между основными фигурами стереометрии (точкой и плоскостью, прямой и плоскостью, плоскостями).
Измерение расстояний между различными физи- 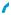
 ческими объектами является одним из самых рас-
ческими объектами является одним из самых рас-  пространённых видов математической деятельности человека. Если размерами объекта можно пренебречь, то речь
пространённых видов математической деятельности человека. Если размерами объекта можно пренебречь, то речь
идет об измерении расстояний между точками, то есть об определении длин отрезков. В других случаях моделирование данных объектовспомощьюточекприизмерениирасстояниймеждуними нецелесообразно или бессмысленно, например, когда речь идет об измерении расстояния между электролампой и столом (рис. 480), если первую можно отождествлять с точкой, то для моделирования стола более пригодна плоскость или ее часть. Аналогичная ситуация возникает при определении расстояния между фасадами зданий (рис. 481), что при математическом моделировании сводится к определению расстояния между параллельными плоскостями; при установлении вертикального рельса на определенном расстоянии от стены (рис. 482) (определение расстояния между параллельными прямой и плоскостью) и т. п.
Измерение расстояний в пространстве |
441 |
Рассмотрим вопрос об измерении расстояний между самыми простыми фигурами в пространстве. Содержание понятия рассто- яния остаётся таким же, как и в планиметрии. Например, рассто- яние d от точки А до прямой а — это кратчайшее расстояние меж- ду этой точкой и точками прямой (рис. 483), а расстояние между параллельными прямыми а и b — это длина d кратчайшего из отрезков, соединяющих точки этих прямых (рис. 484).
Такое же содержание имеет и общее понятие расстояния меж- ду фигурами. Например, измерение расстояния d от пункта А до озера В (рис. 485), расстояния d между озёрами A и В (рис. 486) сводится к измерению кратчайшего отрезка, соединяющего точки этих обьектов.
Обобщение понятия расстояния между фигурами в пространс- тве не вызывает затруднений.
Расстоянием между фигурами называют длину кратчайшего из отрезков, соединяющих точки дан ных фигур.
Если фигуры пересекаются, то будем считать, что расстояние между ними равно нулю. Это и понятно, так как фигуры в целом «не удалены» друг от друга. Для фигур, не имеющих общих точек, расстояние между ними является одной из мер их взаимного рас- положения.
Понятно,чтозадачанахождениярасстояниймеждупроизволь- ными геометрическими фигурами является слишком общей, а потому ограничимся детальным рассмотрением расстояний меж- ду простейшими фигурами пространства — точками, прямыми, плоскостями. Как и в планиметрии, эти расстояния реализуются через длины соответствующих перпендикуляров. Кроме того, к указанным ситуациям часто сводится задача об измерении рас- стояний между более сложными фигурами.

442 |
Перпендикулярность прямых и плоскостей |
Теорема 1 (о расстоянии от точки до плоскости).
Расстояние от точки до плоскости равно длине перпендикуляра, проведенного из данной точки на данную плоскость.
Этосвойстворасстоянияотточкидоплос- кости непосредственно вытекает из свойс- тва наклонных и перпендикуляров. Дейс- твительно, перпендикуляр, проведенный
из точки к плоскости, меньше наклонных, проведенных из той же точки к плоскости
(рис. 487).
Теорема 2 (о расстоянии между прямой и плоскостью).
Расстояние между прямой и параллельной ей плоскостью равно длине перпендикуляра, проведенного из произвольной точки прямой к данной плоскости.
Обоснование этого свойства о расстоянии между прямой и плос- костью опирается на свойства прямой, параллельной плоскости, и теорему 1 о расстоянии от точки к плоскости.
Действительно, расстояние от каждой точки прямой до плоскости равно длине перпен- дикуляра, проведенного из данной точки к
плоскости. Для точек прямой, параллельной плоскости, эти расстояния являются равны-
ми (рис. 488).
Теорема 3 (о расстоянии между параллельными плоскостя- ми).
Расстояние между параллельными плоскостями равно длине перпендикуляра, проведенного из произвольной точки одной плоскости ко второй плоскости.
Обоснование теоремы 3 аналогично обос- нованию теоремы 2. Отличие заключается лишь в том, что перпендикуляры проводят- ся из всех точек одной плоскости ко второй
(рис. 489).
Приведеннымисвойствамиширокопользу- ются в различных сферах деятельности чело- века, в быту. Например, с их помощью опреде- ляют расстояния от самолета до поверхности
Измерение расстояний в пространстве |
443 |
|
земли, от светильника до пола, от провода линии электропередач |
||
до поверхности земли, между потолком и полом и т. п. |
||
Пример 1. |
Плоскости правильного треугольника ABS и квад- |
|
рата ABCD со стороной а перпендикулярны, точки L, K, M явля- |
||
ються серединами соответственно сторон DC, AB, AS. Найти рас- |
||
стояние: |
|
|
1) от точки А до прямой ВS; |
|
|
2) от точки А до плоскости SBC; |
|
|
3) от прямой |
AD до плоскости SBC; |
|
4) между плоскостями MKL и SBC. |
|
|
1)РасстояниеотточкиАдопрямойBS рав- |
||
нодлинеперпендикуляра,проведенногоизточ- |
||
ки А к прямой BS в плоскости ABS. Поскольку |
||
треугольник ABS — правильный, то таким пер- |
||
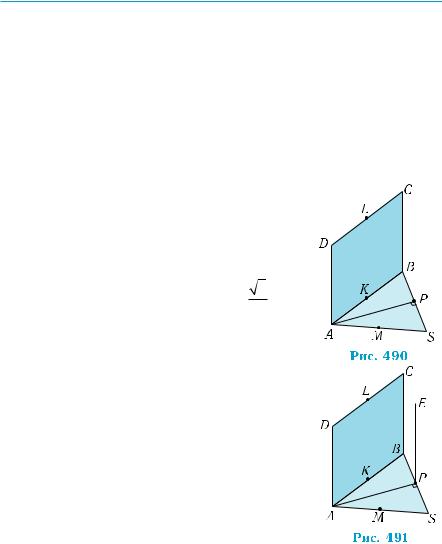
пендикуляром будет медиана АР |
этого тре |
|
угольника (рис. 490). Её длина равна |
3 a. |
|
|
|
2 |
2) Расстояние от точки А до плоскости SBC |
||
равно, по свойству расстояния от точки до |
||
плоскости (теорема 1), длине перпендикуля- |
||
ра, проведенного из точки А к плоскости SBC. |
||
Этим перпендикуляром будет отрезок АР, где |
||
Р — середина стороны SB (рис. 490). Действи- |
||
тельно, отрезок АР перпендикулярен стороне |
||
SB треугольника ABS, так как он является |
||
медианой правильного треугольника. Прямая |
||
ВС перпендикулярна плоскости ABS, ибо она |
||
лежит в одной из перпендикулярных плоскос- |
||
тей и перпендикулярна линии их пересече- |
||
ния. Проведем через точку Р прямую РЕ, па- |
||
раллельную прямой ВС (рис. 491). Она лежит |
||
в плоскости |
SBC (почему?) и перпендикуляр- |
|
на плоскости ABS, по теореме о двух параллельных прямых, одна |
||
из которых перпендикулярна плоскости (теорема 1 § 19): ВС || РЕ, |
||
ВС ABS. Поэтому РЕ ABS. По определению прямой, перпен- |
||
дикулярной плоскости, РЕ АР. По признаку перпендикулярнос- |
||
ти прямой и плоскости (теорема 1 §18), АР SBС. Длина перпен- |
||
444 |
|
Перпендикулярность прямых и плоскостей |
|
дикуляра АР равна |
3 |
a. Это и является искомым расстоянием от |
|
2 |
|||
|
|
||
точки А до плоскости SBC. |
|||
3) Прямая AD и плоскость SBC параллельны, по признаку па- раллельности прямой и плоскости (теорема 1 § 11): AD||ВС. Поэто-
му искомое расстояние, по свойству расстояния между прямой и |
||||
плоскостью (теорема 2), равно расстоянию от точки А |
плоскости |
|||
SBC и, по предыдущему заданию, равно |
3 |
a. |
|
|
2 |
|
|
||
|
|
|
|
|
4) Плоскости MKL и SBC параллельны, по признаку парал- |
||||
лельности плоскостей (теорема 1 §12): KМ || BC (KМ — средняя |
||||
линия треугольника ABS), KL || BC (KL — отрезок, соединяющий |
||||
середины параллельных сторон квадрата |
ABCD), |
поэтому |
||
MKL || SBC. Следовательно, искомое расстояние, по свойству рас-
стояния между параллельными плоскостями (теорема 3), равно
длине перпендикуляра, проведенного из произвольной точки |
|||||||||||||||
плоскости MKL |
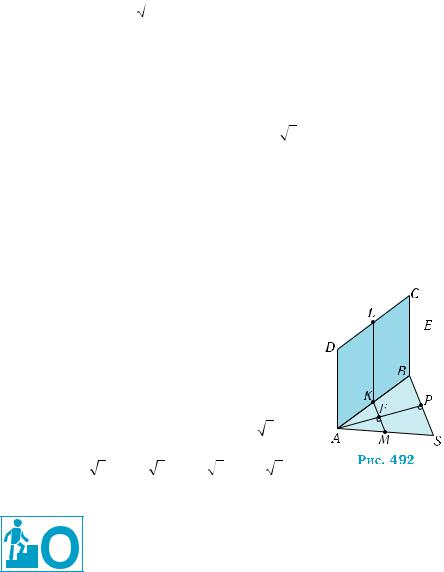
к плоскости SBC. Возьмем точ- |
||||||||||||||
ку пересечения |
F отрезков |
MK и АР (рис. 492). |
|||||||||||||
Поскольку АР |
является перпендикуляром к |
|
|
||||||||||||
плоскости SBC (см. задание 2), то FP — перпен- |
|
|
|||||||||||||
дикуляр к этой плоскости. Его длина равна |
|
|
|||||||||||||
1 AP , так как средняя линия треугольника де- |
|
|
|||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лит медиану, которую она пересекает, пополам |
|
|
|||||||||||||
|
|||||||||||||||
(почему?). Искомое расстояние равно |
|
3 |
a. ■ |
||||||||||||
|
4 |
||||||||||||||
Ответ: 1) |
3 |
a; 2) |
3 |
a; |
3) |
3 |
a; 4) |
|
3 |
a. |
|||||
2 |
2 |
2 |
4 |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
Рассмотримболеедетальнодоказательствосвойстврас- стояний в пространстве. Поскольку теорема 1 является прямым следствием свойств наклонных и перпендику-
ляров,рассмотримдоказательствотеоремы2.
Доказательство теоремы 2
Пусть имеем прямую l и параллельную ей плоскость α (рис. 493). Поскольку расстояние между прямой l и плоскостью α — это длина кратчайшего отрезка, соединяющего их точки, то длина наклонной, соединяющей точки прямой и плоскости, не

Измерение расстояний в пространстве |
445 |
может быть искомым расстоянием. Докажем, что длины всех перпендикуляров, проведен- ных из точек прямой l к плоскости α, равны
между собой. А потому расстояние между прямой и плоскостью равно длине каждого из таких перпендикуляров.
Проведем из двух точек А и В прямой l перпендикуляры АA1 и ВB1 к плоскости α.
Поскольку прямые, перпендикулярные одной плоскости, парал- лельны между собой (теорема 2 § 19), то через прямые АA1 и ВB1 можно провести плоскость, содержащую l. Пряма A1B1 является линией пересечения этой плоскости с плоскостью α (почему?). Од- нако в этом случае АВ || А1В1 , то есть четырехугольник АА1В1В является параллелограммом (даже прямоугольником). Отсюда
АА1 = ВB1. ■
Доказательство теоремы 3 аналогично доказательству преды- дущей теоремы.
Доказательство теоремы 3
Как и в теореме 2, наклонная, соединяющая две точки па- раллельных плоскостей, не может определять расстояние меж- ду ними. А все перпендикуляры, проведенные из точек одной из плоскостей ко второй, параллельны, по теореме о параллельности прямых, перпендикулярных плоскости (теорема 2 § 19). Кстати, они одновременно перпендикулярны обеим плоскостям, по теоре- ме о параллельных плоскостях, одна из которых перпендикуляр- на прямой (теорема 3 § 19).
Пусть α и β — параллельные плоскости, а АА1 и ВВ1 — два произвольных перпенди- 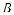
куляра, соединяющие точки этих плоскостей 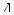 (рис. 494). Они параллельны, а потому рав-
(рис. 494). Они параллельны, а потому рав- 

ны, по теореме об отрезках параллельных 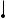 прямых между параллельными плоскостями
прямых между параллельными плоскостями 
 (теорема 4 § 12). Можно и непосредственно
(теорема 4 § 12). Можно и непосредственно 
 доказать равенство этих отрезков, рассмотрев
доказать равенство этих отрезков, рассмотрев 


 четырехугольник АА1В1В, как это было сдела- но при доказательстве теоремы 2. ■
четырехугольник АА1В1В, как это было сдела- но при доказательстве теоремы 2. ■
С помощью понятия расстояния можно характеризовать парал- лельность прямой и плоскости, параллельность плоскостей. При этом справедливыследующиеутверждения,обратныетеоремам2и3.
446 |
Перпендикулярность прямых и плоскостей |
Теорема 4 (признак параллельности прямой и плоскости).
Если все точки прямой лежат на одинаковом, отличном от нуля, расстоянии от плоскости, то прямая и плоскость параллельны.
Теорема 5 (признак параллельности плоскостей).
Если все точки одной плоскости лежат на одинаковом, отличном от нуля, расстоянии от второй плоскости, то эти плоскости параллельны.
Действительно, при выполнении условий этих утверждений соответствующие фигуры не могут иметь общих точек, иначе бы расстояние между ними равнялось нулю.
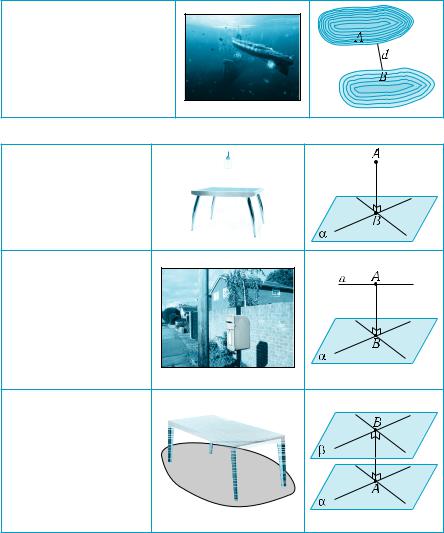
Утверждения будут правильными, если условия выполняются не для всех точек, а для нескольких. В первом утверждении до- статочно допустить, что условие выполняется для двух точек пря- мой, во втором — для трех точек, не лежащих на одной прямой (рис. 495, 496). Попробуйте доказать это самостоятельно. Приве- денные утверждения широко используются в практике как при- знаки параллельности прямой и плоскости, двух плоскостей. Так, параллельность поверхности стола полу обеспечивается одинако- вой длиной его ножек.
Пример 2. |
В тетраэдре SABC основание |
||
АВС — равносторонний треугольник со сто- |
|||
роной 6 см, боковые грани SAB, |
SAC, SBC — |
||
равнобедренные треугольники |
с боковым |
||
ребром 5 см. Найти расстояние от центра О |
|||
основания до плоскости боковой грани. |
|||
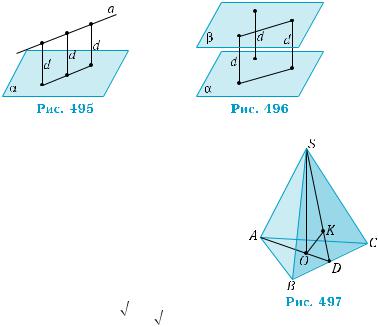
Расстояние от точки О до плоскости SBC |
|||
равно длине перпендикуляра ОK из точки О |
|||
к плоскости SBC (рис. 497). Точка О лежит на |
|||
пересечении медиан (и высот!) треугольника |
|||
АВС,причем OD = 1 AD = |
6 3 = |
3 .Посколь |
|
|
3 |
3 2 |
|
Измерение расстояний в пространстве |
447 |
ку в треугольнике SBC медиана SD также является высотой, то |
|
SD BC, поэтому BC ODC |
и SBC ODC. Следовательно, пер- |
пендикуляр из точки О на плоскость BSC совпадает с перпенди- |
|||
куляром ОK из точки О на прямую SD, являющейся линией пере- |
|||
сечения плоскостей |
SAD |
и |
SBC. По теореме Пифагора, |
SD = SB2 − BD2 = 52 |
−32 = 4 |
(см).Посколькуортогональные про |
|
екции боковых рёбер на основание одинаковы, то S ортогонально |
|||
проектируется в центр описанной около треугольника АВС ок- ружности, то есть в точку О. Поэтому треугольник SOD — прямо-
угольный. По теореме Пифагора, имеем: SO = SD2 −OD2 =
= 16 −3 = 13 (см). Нетрудно увидеть (докажите это, пользуясь подобием треугольников или различными формулами площади
треугольника), что OK = (SO · OD) : SD = ( 13 3):4 = |
39 |
(см). |
|
4 |
|
||
|
до дру- |
||
Понятно, учитывая симметрию, что расстояния от точки О |
|||
гих боковых граней такие же. ■ |
|
|
|
439 см.
99 |
Контрольные вопросы |
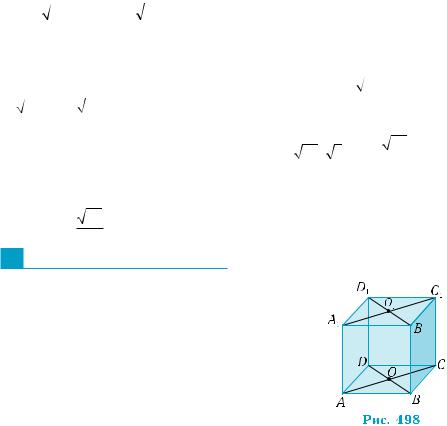
1. |
На рис. 498 изображен куб ABCDA1B1C1D1; |
|
точки О, О1 — центры граней ABCD и |
|
A1B1C1D1. |
|
1) Какая из точек A1, О1, В1 лежит ближе к |
|
плоскости АВС? |
|
2) Какие из рёбер куба наиболее удалены |
|
от плоскости АА1В1В? |
|
3) Какое из расстояний больше: от прямой |
|
АО1 до плоскости DCC1 или от прямой AD1 |
|
до плоскости BDС1? |
2. |
4) Чему равно расстояние между плоскостями ADD1 и ВСС1? |
Пусть прямая а параллельна плоскости α. Могут ли точки |
|
|
прямой а находиться на различных расстояниях от точек |
3. |
плоскости α? |
Верно ли, что если расстояние от прямой до плоскости отлич- |
|
4. |
но от нуля, то прямая и плоскость параллельны? |
Известно, что отрезок AB удален от плоскости α на 3 см. Озна- |
|
5. |
чает ли это, что прямая AB удалена от плоскости α на 3 см? |
Верно ли, что две плоскости совпадают, если расстояние меж- |
|
|
ду ними равно нулю? |
448 |
Перпендикулярность прямых и плоскостей |
6.Верно ли, что расстояние от отрезка до плоскости равно рас- стоянию от одного из его концов до этой плоскости?
7.Все стороны треугольника АВС находятся на расстоянии 3 от плоскости α. Параллельны ли плоскости АВС и плоскость α?
8.Какую фигуру образуют точки, равноудаленные от данной плоскости?
9.Как нужно закреплять провод на столбах, чтобы обеспечить его параллельность к поверхности земли?
10.Как измерить высоту дерева, не поднимаясь на его верхушку?
Графические упражнения
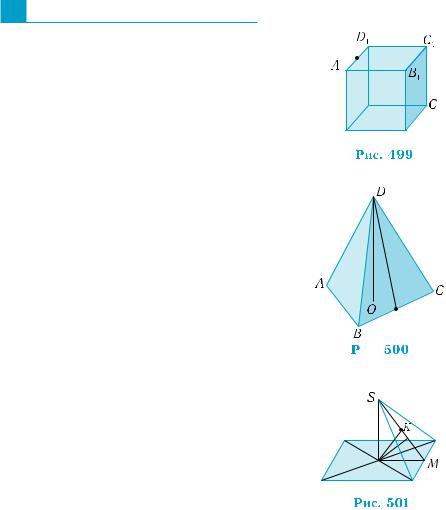
1.Нарис.499изображенкубABCDA1B1C1D1
сребром а, точки М, М1 — середины рё- 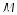 бер АD, А1D1 соответственно. Найдите
бер АD, А1D1 соответственно. Найдите 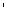 расстояние:
расстояние:
1)от точки А до прямой АВ; 
2)от точки D1 до прямой АВ; 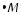
3)от точки А1 до плоскости ВСС1В1; 
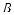
4)от точки А1 до плоскости АВ1С1В;
5)от точки М до плоскости AB1C1D;
6)от прямой A1D1 до плоскости AB1C1D;
7)от прямой AD1 до плоскости AB1C1D;
8)между плоскостями AA1D1 и BB1C1.
2.На рис. 500 изображен правильный тетраэдр ABCD, F — середина ВС, О — центр грани АВС. Длина какого отрезка
равна расстоянию: 
1)от точки D до плоскости АВС; 
2)от точки D до прямой ВС; 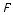
3)от точки С до плоскости АОВ?
3.Из центра О квадрата ABCD (рис. 501) 
 проведен перпендикуляр OS к плоскости квадрата. Точка М — середина ВС, Р — основание высоты треугольника OMS,
проведен перпендикуляр OS к плоскости квадрата. Точка М — середина ВС, Р — основание высоты треугольника OMS, 
его медиана. Длине какого отрез- ка равно расстояние: 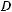

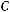
1)от точки O до плоскости BCS; 

2)от точки S до плоскости АВС; 
3)от точки С до плоскости BDS? 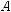
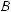 OK —
OK —

Измерение расстояний в пространстве |
449 |
Задачи
462. |
ТочкаD находитсянарасстоянии8смотвершинравносторон- |
||||
|
него треугольника ABC со стороной 4 см. Найдите расстояние: |
||||
|
1°) от точки B |
до плоскости DOC, где O — центр треуголь- |
|||
|
ника ABC; |
до плоскости ABC; |
|
||
|
2°) от точки D |
|
|||
|
3) от плоскости, проходящей через середины отрезков DA, |
||||
463. |
DB, DC, до плоскости треугольника ABC. |
||||
Пусть точка O |
является серединой катета AC прямоугольно- |
||||
|
го равнобедренного треугольника с гипотенузой AB = 4 см; |
||||
|
OP — перпендикуляр к плоскости треугольника длиной |
||||
|
2 см. Найдите расстояние: |
|
|
|
|
|
1°) от точки B до плоскости AOP; |
|
|||
|
2°) от плоскости, проходящей через середины сторон CB и |
||||
|
AB параллельно OP, до плоскости |
CPA; |
|||
|
3) от точки O до плоскости PAB. |
|
|||
464°. Из точки K — середины гипотенузы АВ равнобедренно- |
|||||
|
го прямоугольного треугольника |
АВС с катетами длиной |
|||
|
8 см — проведен перпендикуляр |
KS к плоскости треуголь- |
|||
|
ника. Длина KS составляет 6 см. Найдите расстояние: |
||||
|
1) от точки С до плоскости |
АKS; |
|
||
|
2) от точки А до плоскости |
KСS; |
|
||
|
3) от точки S до прямой ВС. |
|
|||
465. Дан куб ABCDA1B1C1D1 с ребром а. Найдите расстояние: |
|||||
|
1°) от точки А1 |
до плоскости BDD1; |
|
||
|
2°) от прямой |
B1D1 до плоскости АВС; |
|||
|
3°) между противоположными гранями куба; |
||||
|
4°) от точки А1 |
до прямой BD; |
|
||
|
5) между прямыми AD1 иСС1; |
|
|||
|
6*) от точки А1 до плоскости AB1D1; |
||||
|
7*) между плоскостями CD1B1 и DA1B. |
||||
466. ТочкаМлежитнарасстоянииb отвсехвершинквадратаАВСD |
|||||
|
со стороной а и центром в точке О. Найдите расстояние: |
||||
|
1°) от точки М |
до плоскости |
АВС; |
|
|
|
2°) от точки А до плоскости |
ВМD; |
|
||
3)от точки О до плоскости МСD, если b = 23 a ;
4)от точки М до прямой СD;
5)между прямыми ОМ и АD.
467.Концы отрезка удалены от некоторой плоскости на 1 см и 4 см. Найдите расстояние от середины отрезка до плоскости.

450 |
Перпендикулярность прямых и плоскостей |
468. Катеты прямоугольного треугольника равны 16 см и 12 см. На каком расстоянии от плоскости треугольника лежит точка,
удаленная от каждой вершины треугольника на 10 2 см? 469. Сторона равностороннего треугольника равна 6 см. На ка-
ком расстоянии от плоскости треугольника расположена точка, удалённая на 9 см от:
1) сторон треугольника;
2*) каждой из прямых, содержащих стороны треугольника?
470°. Если из двух точек, находящихся на различных расстояни- ях от плоскости, провести к этой плоскости равные наклон- ные, то большей будет проекция наклонной, проведенной из более близкой к плоскости точки. Докажите это.
471. Если из точки А, находящейся вне плоскости α, опустить перпендикуляр на эту плоскость, а из его основания провес- ти перпендикуляр к прямой ВС, лежащей в плоскости α, то плоскость, проходящая через эти перпендикуляры, будет перпендикулярна прямой ВС. Докажите это.
472*.Плиту прямоугольной формы подняли краном так, что три её вершины удалены от поверхности земли, соответственно, на 2 м, 3 м и 4 м. На каком расстоянии от земли находится четвертая вершина?
473*.Точка А удалена от сторон угла, равного 60°, на 20 см и 7 см, а от его вершины — на 25 см. Найдите расстояние от точки А до плоскости угла.
474*.Точка, лежащая вне плоскости прямого угла, находится на расстоянии 4 см от каждой из его сторон. Найдите расстоя- ние от точки до вершины угла, если точка удалена от плос-
кости угла на 7 см.
475. Плоскости квадрата АВСD и равностороннего треугольника АВМ взаимно перпендикулярны, АВ = а. Постройте общий перпендикуляр к прямой АС и к медиане МО треугольника и определите длину этого перпендикуляра.
476. Пусть АВ — общий перпендикуляр к скрещивающимся пря- мым а и b. Точки A и С лежат на прямой а, точки В и D — на прямой b; АС = ВD. Докажите, что АСВ = ВDС.
Упражнения для повторения
477.В одной полуплоскости, ограниченной прямой АВ, построе-
ны углы: ВАС = 38°, САD = 68°, DАЕ = 85°, ЕАK = 99°.
Определите KАС.
Измерение расстояний в пространстве |
451 |
478.Один из смежных углов втрое больше разности между ними. Определите их градусную меру.
479.Наблюдатель, находящийся на берегу озера на высоте h над уровнем воды, видит тучку под углом α, а ее отображение — под углом β к горизонту. Найдите высоту тучки над поверх-
ностью озера при α = 53°27', β = 55°42', h = 76,8 м.
Итог
Основное определение
Расстоянием между
произвольными фигу-
рами называют длину кратчайшего из отрез- ков, соединяющих точки данных фигур.
Свойства расстояний
Расстояние от точки до плоскости равно длине перпендику- ляра, проведенного из данной точки к данной плоскости.
Расстояние между прямой и параллель- ной ей плоскостью равно длине перпен- дикуляра, проведен- ного из произволь- ной точки прямой к данной плоскости.
Расстояние между па- раллельными плос- костями равно длине перпендикуляра,про- веденного из произ- вольной точки одной плоскости ко второй плоскости.
