
- •Обращение к читателю
- •Введение
- •РАЗДЕЛ 1. Функции, их свойства и графики
- •§1. Числовые множества
- •§2. Вычисления и расчёты
- •§3. Функциональные зависимости
- •§4. Основные свойства функций
- •§5. Корни n-ой степени
- •§6. Степенные функции с рациональными показателями
- •§7. Основные понятия и аксиомы стереометрии
- •§8. Взаимное расположение двух прямых в пространстве
- •§9. Параллельное проектирование
- •§10. Изображение фигур в стереометрии
- •§11. Параллельность прямых и плоскостей
- •§12. Параллельность плоскостей
- •§13. Тригонометрические функции числового аргумента
- •§14. Основные соотношения между тригонометрическими функциями
- •§15. Свойства и графики тригонометрических функций
- •§16. Тригонометрические формулы сложения и следствия из них
- •§17. Простейшие тригонометрические уравнения и неравенства
- •§18. Перпендикулярность прямой и плоскости
- •§19. Связь между параллельностью и перпендикулярностью прямых и плоскостей
- •§20. Перпендикулярность плоскостей
- •§21. Ортогональное проектирование
- •§23. Измерение расстояний в пространстве
- •§24. Измерение углов в пространстве
- •Ответы и указания к задачам
- •Предметный указатель
- •Содержание
§15. свойства и графики тригонометрических функций
В этом параграфе будут рассмотрены свойства тригономет рических функций, построены их графики. Будет рассматри ваться специфическое свойство этих функций — периодичность. Периодические функции описывают различные ситуации (аст рономические явления, жизнедеятельность организма и т. п.), периодически повторяющиеся. Ðассматриваются гармонические колебания, описывамые тригонометрическими функциями.
1. Периодические функции
При введении тригонометрических функций аргу- 
 мент обозначался буквой t, поскольку буквы х и у
мент обозначался буквой t, поскольку буквы х и у  использовались для обозначения координат точки Pt. Теперь вернемся к привычным обозначениям: х — независимая переменная, у — зависимая переменная, то есть у = sin х,
использовались для обозначения координат точки Pt. Теперь вернемся к привычным обозначениям: х — независимая переменная, у — зависимая переменная, то есть у = sin х,
у = cos х, у = tg x.
Так как числам х, х ± 2π на тригонометрической окружности соответствует одна и та же точка Px, то имеют место равенства:
sin(x ± 2π)= sin x, cos(x ± 2π) = cosx .
Это свойство функций у = sin х и у = cos х называют периодичностью. Оно заключается в том, что значения функции повторяются через равные промежутки изменения аргумента. Точный смысл понятия периодичности функции содержится в следующем определении.
Функция у = f(х) называется периодической, если существует такое число T ≠ 0, что область определе-
ния функции вместе с каждой точкой х содержит точки х ± Т и при этом выполняется равенство f(х ± Т) = f(x). Число Т называется периодом функции.

Свойства и графики тригонометрических функций |
277 |
!Обращаем внимание на то, что равенство f(х ± Т) = f(х) должно выполняться для всех значений х из области определения функции. Для отдельных функций можно указать числа, прибавление которых к одному значению аргумента не меняет значения функции, в то же время прибавление к другому значению аргумента — меняет. Такие числа не являются периодами функции.
π |
|
= sin |
3π |
= −1 |
, |
|
Например, sin 0 = sin (0 + π) = 0, но уже sin |
2 |
+ π |
2 |
|||
|
|
|
|
|
||
а sin π2 =1 . Следовательно, число π не является периодом функ-
ции у = sin х.
Функции у = sin х и у = cos х является периодическими с периодом 2π. Этот факт использовался в § 14 при вычислении значений синуса и косинуса.
Периодом тангенса и котангенса является число π, что вытекает из формул приведения: tg(t + π) = tg(t – π) = tg t.
Если число Т является периодом функции у = f(x), то числа 2Т, 3Т, ..., и вообще пТ, п Z, п ≠ 0, также являются ее периодами. Действительно, например, f(x + 2Т) = f((x + Т) + Т) = f(x + Т) = f(x). Отсюда вытекает, что периодами функций у = sin х и у = cos х являются числа 4π, 6π, ..., а периодами функций у = tg х и у = ctg х являются числа 2π, 3π, 4π, ... .
На графике функции ее периодичность с периодом Т отображается следующим образом.
Если график периодической функции с периодом Т параллельно перенести на Т единиц вдоль оси абсцисс в положительном или отрицательном направлениях, то он перейдет сам в себя.
На рис. 305 изображен график периодической функции с периодом l.
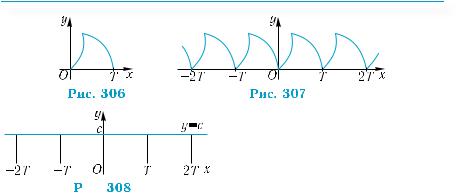
Для построения графика периодическойфункцииспериодом
Т достаточно построить его на отрезке длиной Т (рис. 306), а затем
построенный график параллельно перенести вдоль оси абсцисс в обоих направлениях на расстояния Т, 2Т, 3Т и т. д. (рис. 307).
278 |
Тригонометрические функции |
Постоянная функция, определённая на всей числовой оси является периодической. Ее пе-
 риод — любое число, отличное от нуля. Действительно, для посто-
риод — любое число, отличное от нуля. Действительно, для посто- 
 янной функции у = с выполняет-
янной функции у = с выполняет-
ся очевидное соотношение: у(х + Т) = с = у(х) для любого действительного х при любом Т ≠ 0 (рис. 308).
Периодическими функциями описываются различные физические процессы: малые колебания маятника, вращения планет вокруг Солнца, сила переменного тока и т. п. Самым простым прибором для иллюстрации периодических процессов являются механические часы. Положения концов стрелок повторяются через равные промежутки времени. Для секундной стрелки этот промежуток составляет 60 с, для минутной — 60 мин, для часовой — 12 ч.
Пример 1. Пусть функция у = f(x) является периодической с периодом 3 и f(1)= 2. Чему равняется f(– 8)?
Во-первых, отметим, что функция у = f(x) определена при х = –8, так как, по определению периодической функции, область определения данной функции вместе с точкой х = 1 содержит точ-
ки: 1 – 3 = –2, –2 – 3 = –5, –5 – 3 = –8. Во-вторых, f(–8) = f(–8 + 3) = = f(–5) = f(–5 + 3) = f(–2)= f(–2 + 3) = f(1) = 2.
Ответ. 2.
Пример 2. Доказать, что периодом функции у = sin2x является число π.
Функция у= sin2x определена на всей числовой оси. Поэтому ее область определения вместе с каждой точкой х содержит точки х ± π. Подставим вместо х в выражение для этой функции х + π: sin (2(x + π)) = sin (2x + 2π) = sin 2x. Такой же результат получим,
если вместо х в выражение для этой функции подставить х – π. По определению, число π является периодом функции у = sin2x.

Свойства и графики тригонометрических функций |
279 |
Из того, что каждой точке на тригонометрической окружности соответствует бесконечное множество чисел,отличающихсядруготдругана2πk,k Z,вытекает, что тригонометрические функции у = sin х и
у = cos х для чисел х + 2πk при всех k Z принимают одно и то же значение: sin (х + 2πk) = sin х, cos(x + 2πk) = cos х, то есть пе-
риодами функций у = sin х и у = cos х являются числа 2πk, k ≠ 0, k Z. Все эти периоды кратны 2π. Естественно возникает вопрос: «Существуют ли другие положительные периоды этих функций, меньшие 2π?» Ответ на него дает следующее утверждение.
Теорема 1. Наименьший положительный период функций
у = sin х и у = cosх равен 2π.
Покажем, что других периодов, кроме чисел 2πk, k ≠ 0, k Z,
эти функции не могут иметь. Действительно, если Т — период функции у = sin х, то sin (x + T) = sin x для любого х, в частности для х = 0, то есть sin T = sin 0 = 0. Но sin Т обращается в нуль при Т = 0; Т = π; Т = 2π и, вообще, при Т = пπ, п Z, и только при этих
значениях.
Число π не является периодом рассматриваемой функции.
Действительно, |
sin |
π |
π |
|
= |
sin |
3π |
= −1 |
, то есть сущест- |
|
2 |
=1, sin |
2 |
+ π |
2 |
||||||
|
|
|
|
|
|
|
|
|||
вует значение х из области определения функции, такое, что sin (x + π) ≠ sinx. Следовательно, наименьшим положительным периодом функции у = sin х является число 2π.
Доказательство того, что 2π — наименьший положительный период косинуса, аналогично.
Подобное утверждение справедливо для функций у = tg х и у = сtg х.
Теорема 2. Наименьший положительный период функций у = tg х и у = сtgх равен π.
Из формул приведения вытекает, что числа πk, k ≠ 0, k Z, являются периодами функций у = tg х и у = ctg х. Поскольку tg х
при |
|
π |
π |
|
обращается в нуль при х = 0 или при х = π |
||
x 0; |
2 |
|
|
2 |
; π |
||
|
|
|
|
|
|
||
и только в этих точках, то не существует положительного числа, меньшего π, которое могло бы быть периодом тангенса. Следовательно, наименьшим положительным периодом функции у = tg х
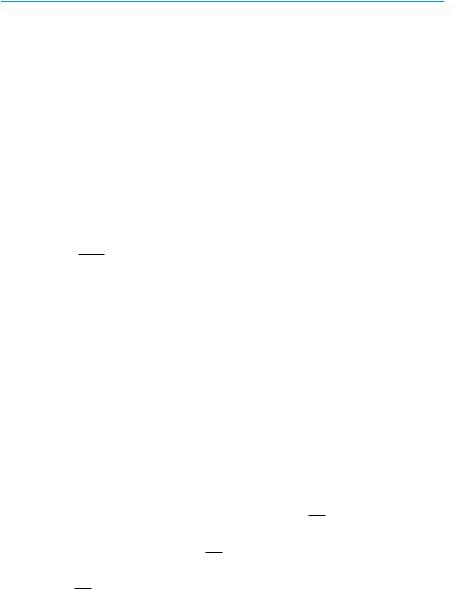
280 |
Тригонометрические функции |
является число π. Доказательство того, что π — наименьший положительный период котангенса, аналогично. Рекомендуем провести его самостоятельно.
Наименьший положительный период периодической функции называют основным периодом этой функции. Все другие ее периоды кратны основному периоду. Для функций у = sinx и у = cos х основной период равен 2π, а для функций у = tg х и у = ctg х основной период равен π. Простейшим примером периодической функции, не имеющей основного периода, является постоянная функция, определенная на всей числовой оси.
Пример 3. Найти основной период функции у = sin 3х.
Областью определения данной функции является числовая ось. Числа 2π3n , nZ, — периоды для функции у = sin3x:
sin3 |
|
2πn |
= sin(3x + 2πn) = sin3x . |
|
x + |
3 |
|
||
|
|
|
|
|
Если Т — произвольный положительный период для sin3x, то sin3(x + Т) = sin3x при каждом х, поскольку число 3Т также явля-
ется |
|
периодом |
данной |
функции. |
Беря |
|
x = |
π |
, будем иметь: |
|||||||||
|
|
π |
|
|
|
π |
|
|
|
|
π |
|
|
|
|
|
6 |
|
sin3 |
= sin |
=1 |
, или |
|
= |
1 |
. Однако, sin x равня- |
|||||||||||
|
6 |
+T |
2 |
sin |
2 |
+ 3T |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ется единице |
лишь при x = |
π |
+ 2πn, n Z . Поэтому |
π |
+3T = |
||||
|
|
|
|
|
2 |
|
2πn |
2 |
|
= |
π |
+ 2πn, 3T = 2πn, T = |
2πn ,n Z |
. Среди чисел |
наимень- |
||||
|
2 |
|
|
3 |
|
|
3 |
|
|
шим положительным числом является число 23π , то есть основной период функции sin 3х равен 23π .
Ответ. 23π .
Анализ примера 3 подсказывает следующее свойство периодических функций и содержит идею его доказательства.
Теорема 3. Если функция f является периодической с ос-
новным периодом Т, то функция у = Af(kx + b) + l, где А,

Свойства и графики тригонометрических функций |
281 |
k ≠ 0, b, l — некоторые числа, также является периоди-
ческой, причем ее основной период равен Tk .
Результатрешенияпримера3согласуетсясосформулированным свойством: основной период функции у = sin 3х равен 23π . Из этого свойства вытекает, что основные периоды функций у = sin 4x, y = cos 2x , у = tg 2x соответственно равны 24π = π2 , 2π : 12 = 4π , π2 .
Контрольные вопросы
1°. Верно ли утверждение: если периодическая функция в какойто точке принимает значение 1, то это значение она принимает в бесконечном множестве точек?
2°. Является ли число 3π периодом функции у = sin х? 3°. Является ли число 5π периодом функции у = tg х?
4.Каков основной период функции: а) sin 5х; б) cos 3x ; в) sin πх?
5.Чему равняется f(–9), если функция у = f(x) является периодической с периодом 5 и f(1) = 0?
6*. Является ли функция y = cos x периодической?
7.Может ли быть периодической функция, возрастающая на всей области определения?
2. Свойства и графики функций у = sin х и у = cos х
Рассмотрим простейшие свойства функций у = sin х и у = cos х, пользуясь определениями синуса и коси-
нуса, и построим их графики.
Свойство 1. Функции у = sin х и у = cos х определены на всей
числовой оси.
Действительно, каждому действительному числу х можно поставить в соответствие точку тригонометрической окружности. Абсцисса этой точки равна косинусу числа х, а ордината — синусу числа х.
282 |
Тригонометрические функции |
Свойство 2. Функции у = sin х и у = cos х — периодические с наименьшим положительным периодом 2π.
Это свойство доказано в предыдущем пункте.
Свойство 3. Нулями функции у = sin х являются числа πn, n Z, а нулями функции у = cos х — числа 2π + πn,n Z.
Нули функции у = sin х — это числа, которым на тригонометрической окружности соответствуют точки с ординатой 0, а имен-
но: …, –3π, –2π, –π, 0, π, 2π, 3π, ... и вообще числа πn, n Z. Анало-
гично, нули функции у = cos х — это числа, которым на тригонометрической окружности соответствуют точки с абсциссой 0,
а именно: ..., −32π , − 2π , 2π , 32π ,... и вообще числа π2 + πn,n Z.
Свойство 4. Функция у = sin х — нечёт-
ная, а функция у = cos х — чётная, то есть для каждого х
sin (–х) = – sin х, cos(–х) = cosх.
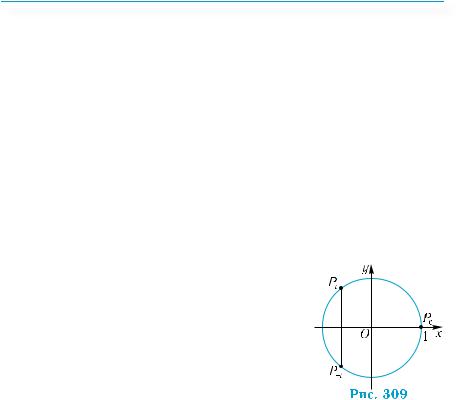
По построению, точки Pt и P-t симметричны относительно оси абсцисс (рис. 309).
Их абсциссы совпадают, а ординаты противоположны. Поэтому при t = x:
sin (–х) = – sin х, cos(–х) = cos х.
Свойство 5. Функция у = sin х положительна на интервале (0; π) и отрицательна на интервале (π; 2π); функция
|
|
|
|
− |
π |
; |
π |
и отрица- |
||||
у = cos х положительна на интервале |
2 |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
π |
; |
3π |
|
|
|
|
|
|
|
|
|
тельна на интервале |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Это свойство обосновано в § 14. |
|
|
|
|
|
|
|
|
|
|||
Свойство 6. Функция у = sin х на промежутке |
|
|
π |
; |
π |
воз- |
||||||
|
− |
2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
растает, а на промежутке |
|
π |
; |
3π |
убывает. Функция |
|
|
2 |
2 |
|
|||
|
|
|
|
|
||

Свойства и графики тригонометрических функций |
283 |
||
у = cos х убывает на промежутке [0; π] и возрастает на |
|||
промежутке [π; 2π]. |
|
|
|
Это свойство вытекает из геометричес- |
|
||
кого смысла синуса и косинуса. Если t растет |
|
||
от − |
π до π , то ордината точки Рt увеличива- |
|
|
ется |
2от – 12от 1 (рис. 310). Если же t растет от |
|
|
π до 3π , то ордината точки Р уменьшается |
|
||
2 |
2 |
t |
|
от 1 до – 1 (см. рис. 310). Если t растет от 0 до |
|
||
π, то абсцисса точки Рt уменьшается от 1 до |
увеличивается |
||
–1. Если же t растет от π |
до 2π, то абсцисса точки Pt |
||
от –1 до 1 (см. рис. 310). |
|
|
|
Свойство 7. Множеством значений функций у = sin х и
у = cos х является отрезок [–1; 1].
По определению синуса, |sin x| ≤ 1. Для произвольного числа
аиз промежутка [–1; 1] существует по крайней мере одна точка тригонометрической окружности, ордината которой равна а. Это означает, что функция у = sin х принимает все значения из промежутка [–1; 1]. Аналогично обосновывается это свойство для функ-
ции у = cos х.
Свойство 8. Функции у = sin х и у = cos х непрерывны на
всей числовой оси.
Действительно, при непрерывном изменении значения х точка Px непрерывно перемещается по тригонометрической окружности, а потому ее координаты cos х и sin х меняются непрерывно.
Построим график функции у = sin х с использованием рассмот-
ренных свойств синуса. Так как эта функция периодическая с
периодом 2π, то достаточно построить график на отрезке [0; 2π], |
||||
длина которого равна периоду синуса. |
|
|
π |
|
Сначала построим график на отрезке |
|
|
|
|
0; |
2 |
. На этом отрезке |
||
|
|
|
|
|
функция у = sin х возрастает, sin 0 = 0, sin π |
=1 . Для нахождения |
|||
|
2 |
|
|
|
284 |
Тригонометрические функции |
нескольких точек графика разобьем отрезок |
|
π |
, например, на |
|
0; |
2 |
|
||
|
|
|
|
|
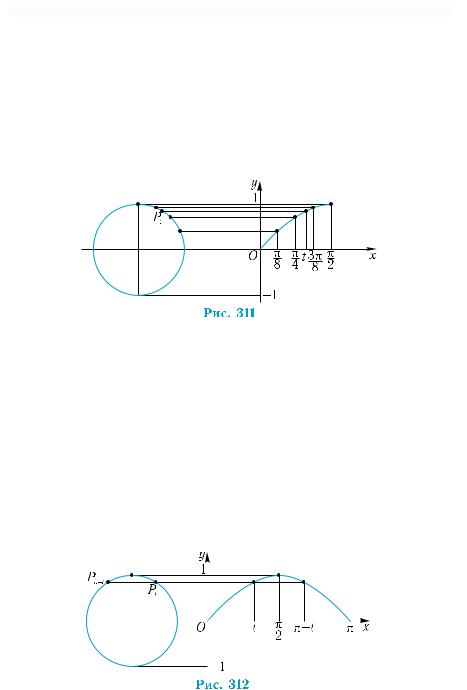
4 равные части. Возьмем единичную окружность с центром в произвольной точке оси абсцисс (для удобства сместим окружность влево (рис. 311)). Для построения точки с абсциссой t найдем на окружности точку Рt и через нее проведем прямую, параллельную оси абсцисс, до пересечения с прямой х = t. Точка пересечения будет принадлежать графику функции у = sin х, так как ее ордината совпадает с ординатой точки Pt и равна sin t.
Построив таким образом все 4 точки графика и соединив их, учитываявозрастаниеинепрерывностьфункции,непрерывнойкривой,
|
|
π |
|
получим эскиз графика функции на отрезке 0; |
(рис. 311). |
|
|
Так как, по формулам приведения, |
|
2 |
|
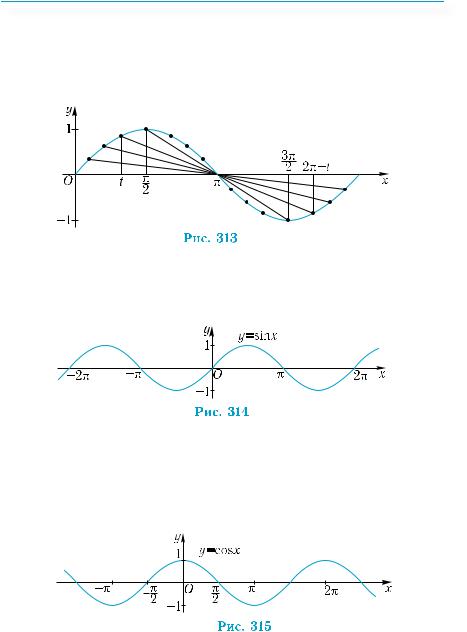
sin(π −t) = sint , то есть орди- |
|||
наты точек t и π – t, симметричных относительно прямой x = π |
, рав- |
||
π |
|
2 |
|
|
|
||
ны между собой, то на промежутке |
;π точки графика функции |
||
2 |
|
|
|
у = sin х располагаются симметрично точкам графика из проме-
жутка |
|
π |
относительно прямой x = |
π |
(рис. 312). |
|||||||
0; |
2 |
|
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Свойства и графики тригонометрических функций |
285 |
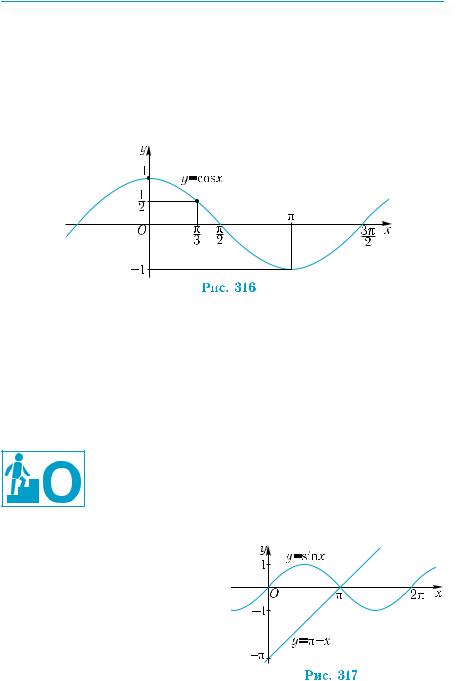
Так как по формулам приведения sin(2π −t) = −sint , то есть ор-
динаты точек t и 2π – t противоположны друг другу, то на промежутке [π; 2π] точки графика функции у = sin х располагаются симметрично точкам графика из промежутка [0; π] относительно точки (π; 0) (рис. 313).
Пользуясь правилом построения графика периодической функции, с помощью параллельных переносов продолжим график на 2π, 4π, 6π, ... вправо и влево вдоль оси абсцисс (рис. 314). Получим график функции у = sin х. Он называется синусоидой.
Так как |
π |
|
, то график функции у = cos х |
|
cos x = sin |
2 |
+ x |
||
|
|
|
|
|
можнопостроитьпараллельнымпереносомграфикафункции у = sin х в отрицательном направлении вдоль оси х
нарасстояние 2π (рис.315).
Пример 4. Найти наибольшее и наименьшее значения функ-
ции у = cos х на промежутке π; 3π .
3 2
286 |
|
|
Тригонометрические функции |
||
|
|
Построим график функции у = cos х, отметив на осе абсцисс |
|||
точки с абсциссами |
π |
и 3π (рис. 316). Найдем на промежутке |
|||
|
π |
|
3π |
3 |
2 |
; |
|
|
|||
|
3 |
точки графика, имеющие наибольшую и наименьшую ор- |
|||
|
|
2 |
|
|
|
динаты. Это соответственно точки с абсциссами 3π и π. Ординаты
этих точек |
|
π |
= cos |
π |
= |
1 |
и |
y(π) = cos π = |
– 1 являются наиболь- |
|
y |
3 |
|
3 |
2 |
||||||
|
|
|
|
|
|
|
|
|||
шим и наименьшим значениями функции на данном промежутке, которые она принимает соответственно в точках 3π и π.
Ответ. 12 ; – 1.
Свойства и графики синуса и косинуса позволяют решать разнообразные задачи, связанные с этими функциями, а именно: «читать» графики, сравнивать значения этих функций, решать уравнения,
неравенства и т. п.
Пример 5. Решить уравнение: sin x = x – π.
В одной системе координат построим графики функций
у = х – π, у = sin х. Они пересе-
каются в одной точке (рис. 317), как видно из графиков. Абсцис-

Свойства и графики тригонометрических функций |
287 |
са π точки пересечения является решением данного уравнения.
Ответ. х = π.
Пример 6. Сравнить числа: 1) sin 2 и sin 3; 2) cos 5 и cos 6; 3) cos 7π и sin 38π .
|
1) Так как |
π |
< 2 < 3 < π , а на отрезке |
π |
|
|
|
функция у = sin x |
|||||||||||
|
2 |
|
|
; π |
|||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
убывает, то sin 2 > sin 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2) Так как |
3π |
< 5 < |
|
|
|
3π |
|
|
|
|
функцияу= cosx |
|||||||
|
2 |
6 < 2π,анаотрезке |
2 |
|
;2 π |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
возрастает, то cos 5 < cos 6. |
|
3π |
|
π |
|
|
π |
|
|
|
π |
|
π |
||||||
|
3) По формуле приведения, sin |
|
− |
|
= |
cos |
. Числа |
||||||||||||
|
8 |
= sin |
2 |
8 |
|
8 |
8 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и |
π |
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
7 |
принадлежат отрезку 0; |
2 |
, на котором функция у = cos х |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
убывает. Так как |
π < |
π , то cos |
π |
> cos π , то есть sin 3π > cos π . |
|||||||||||||||
|
|
|
|
|
8 |
7 |
8 |
|
7 |
|
|
|
|
|
|
8 |
|
7 |
|
|
Ответ. а) sin2 > sin3; б) соs 5 < cos 6; в) sin |
3π > cos π . |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
7 |
|
|
|
|
Рассмотрим построение графиков тригонометрических функ- |
||||||||||||||||||
ций с помощью преобразований графиков функций, изучавших-
ся ранее, а именно: с помощью параллельного переноса графика
вдоль координатных осей, сжатия и растяжения графика, сим- |
|||||||
метричного отображения относительно координатных осей. |
|
|
|
||||
Пример 7. Построить |
графики |
|
|
|
|
π |
|
функций: 1) y = sin x + |
4 |
; |
|||||
2) у = 2 sinx; 3) у = sin 3х. |
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
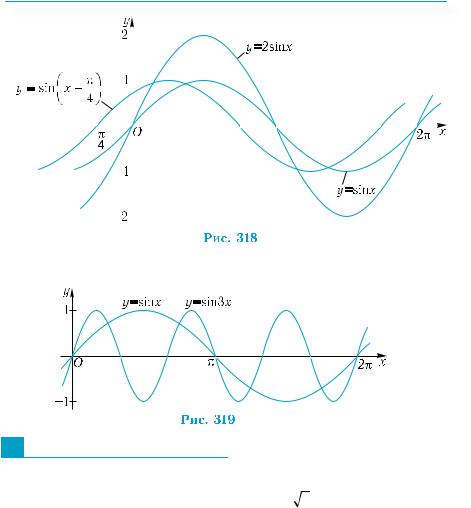
1) График функции |
|
|
|
|
|
|
|
y = sin x + |
4 |
можно получить из гра- |
|||||
|
|
|
|
|
|
|
|
фика у = sinх паралельным переносом вдоль оси х на π |
влево |
||||||
(рис. 318). |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
2) График функции у = 2 sinх построим растяжением графика у = sinх от оси абсцисс в 2 раза (рис. 318).
288 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тригонометрические функции |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) График функции у = sin 3х является результатом сжатия графика у = sin х к оси ординат в 3 раза (рис. 319).
|
Контрольные вопросы |
|
|
|
|
|
||
1°. |
Имеет ли смысл запись: sin 2011? |
|
6 ; в) |
π ; г) |
π ? |
|||
2°. |
Может ли синус числа х равняться: а) |
2 ; б) |
||||||
3°. |
Является ли чётной функция: |
|
|
7 |
2 |
6 |
||
|
|
|
|
|
||||
|
а) у = – cosх; |
б) y = sin2 t ; |
в) y = cos3 t ? |
|
||||
4. |
Какое из чисел: cos 1°, cos 2°, cos 3°, cos 100° является наиболь- |
|||||||
|
шим? |
каких преобразований |
из графика |
функции |
||||
5. |
С |
помощью |
||||||
|
у |
= sin x можно получить график функции: |
г) у = sinx |
+ 3? |
||||
|
а) у = sin(x + 3); б) у = sin3x; |
в) у = 3sinx; |
||||||
6. |
График какой функции получим из графика функции у = cos x: |
|||||||
|
а) параллельным переносом на 2 единицы в положительном |
|||||||
|
направлении вдоль оси абсцисс; |
|
|
|
|
|||

Свойства и графики тригонометрических функций |
289 |
б) параллельным переносом на 2 единицы в отрицательном
направлении вдоль оси ординат; в) сжатием к оси абсцисс в два раза;
г) растяжением от оси абсцисс в два раза?
7. Каковы область определения и множество значений функ- |
||
ции: |
б) у = cos x – 1; |
в) у = cos 2x; |
а) у = sin(x – 1); |
||
г) у = 3 sin x; |
д) у = cos (– х); |
е) у = –sin x? |
8.Что больше: а) sin 6π или sin 8π ; б) cos 40° или cos 75°?
9.Возрастает или убывает функция у = cos х на отрезке:
а) [π ; 2π]; |
б) [0; π ]; |
|
π |
; |
5π |
; |
|
г) [–2; –1]? |
|||
в) |
6 |
6 |
|
|
|||||||
|
|
|
|
|
|
значения функции |
|||||
10*.Каковы наибольшее и наименьшее |
|
|
|||||||||
|
|
|
4π |
|
|
|
|
π |
; |
5π |
|
у = sin x на промежутке: а) 0; |
; б) − |
6 |
? |
||||||||
|
|
|
3 |
|
|
|
|
|
6 |
||
3. Свойства и графики функций y = tg x и y = ctg x |
|||||||||||
|
|
Рассмотрим простейшие свойства функций у = tg x |
|||||||||
|
|
||||||||||
|
|
и у= ctg x, пользуясь их определениями, и построим |
|||||||||
|
|
их графики. |
|
|
|
|
|
|
|
|
|
Свойство 1. Функция у = tg х определена при всех действительных значениях х, кроме x = π2 + πk, k Z , а функция
у = ctg х определена при всех действительных значениях х, кроме x = πk, k Z .
Действительно, функция у = tg х определена при всех значениях х, кроме тех, при которых знаменатель выражения tg х =
=sin x равняется нулю. А условию cos x = 0 как раз и удовлетво- cos x
ряют значения x = π2 + πk, k Z . Аналогично доказывается вторая часть свойства.
Свойство 2. Функции у = tg x и у = ctg x — периодические с наименьшим положительным периодом π.
Это свойство обосновано в п. 1.

290 |
Тригонометрические функции |
Свойство |
3. Нулями функции у = tg х являются числа |
|||||
x = πk, k Z , а нулями функции у = ctg x — |
числа |
|||||
x = π + πk, k Z . |
|
|
|
|||
2 |
|
|
|
|
|
|
Действительно, нули функции у = tg x совпадают с нулями |
||||||
функции |
у = sin х, а нули функции у = ctg x – с нулями функции |
|||||
у = cos х (см. п. 2). |
|
|
|
|||
Свойство 4. Функции у = tg х и у = ctg x — нечётные. |
|
|||||
Действительно, tg(–х) = |
sin(−x) |
= |
−sin x |
= −tg x . |
График |
|
|
|
|||||
|
|
cos(−x) |
cos x |
|
||
функции у = tg х симметричен относительно начала координат. |
|||||||
Так же доказывается это свойство для функции у = ctg x. |
|
||||||
Свойство |
5. Функции у = tg х и у = ctg x положительны на |
||||||
|
|
|
|
|
π |
π |
|
интервале 0; |
|
и отрицательны на интервале |
; π . |
||||
|
|
|
|
|
2 |
2 |
|
Это свойство обосновано в § 14. |
|
||||||
Свойство |
6. Функция у = tg х возрастает на промежутке |
||||||
|
π |
; |
π |
|
|
|
|
− |
2 |
2 |
, а функция у = ctg х убывает на промежутке (0; π). |
||||
|
|
|
|
|
|
||
Это свойство вытекает из определений тангенса и котанген-
са. Если х возрастает от 0 |
до |
π |
, то числитель дроби tg x = |
sin x |
|
|
|
|
2 |
|
cos x |
возрастает, а знаменатель убывает, поэтому функция у = tgx воз- |
|||||
|
|
π |
|
|
|
растает на промежутке 0; |
2 |
. Возрастание функции на проме- |
|||
|
|
|
|
|
|
жутке |
|
− |
π |
|
|
вытекает из нечётности этой функции. Свойство |
|
2 |
;0 |
||||
|
|
|
|
|
|
|
для функции |
у = ctg х вытекает из доказанного и равенства ctg x = |
|||||
=– tg π + x .
2
Свойство 7. Множествомзначенийфункцийу=tgхиу=ctgx
является множество всех действительных чисел.
Свойство 8. Функции у = tg х и у = ctg x непрерывны в своих
областях определения.
Свойства и графики тригонометрических функций |
|
|
|
291 |
Свойства 7 и 8 будут обоснованы позже. |
|
|
||
Рассмотренные свойства функции у |
= tgx позволяют построить |
|||
ее график, как и для функции у = sin |
х, в три этапа. На первом |
|||
этапе построим график на промежутке |
|
π |
|
. Для этого достаточ- |
0; |
2 |
|
||
|
|
|
|
|
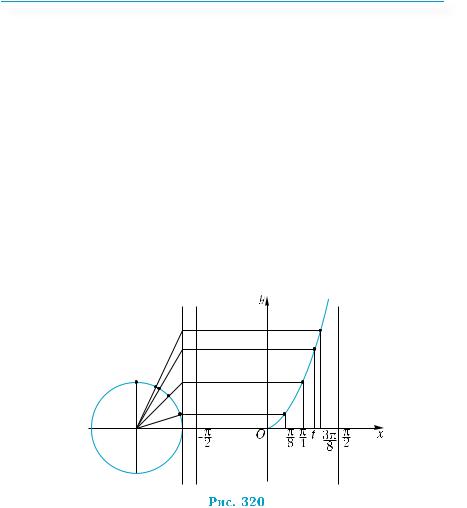
но найти несколько точек графика и соединить их непрерывной линией. Как и при построении синусоиды, разобьем промежуток
|
π |
на 4 равные части. Воспользовавшись линией тангенсов, |
|
0; |
2 |
|
|
|
|
|
|
построим четыре точки (рис. 320), принадлежащие графику фун-
кции у = tgx, х |
|
π |
. Соединив точки (ввиду возрастания и |
|
0; |
2 |
|
||
|
|
|
|
|
непрерывности функции) непрерывной кривой, будем иметь эс-
киз графика функции на промежутке 0; π .
2
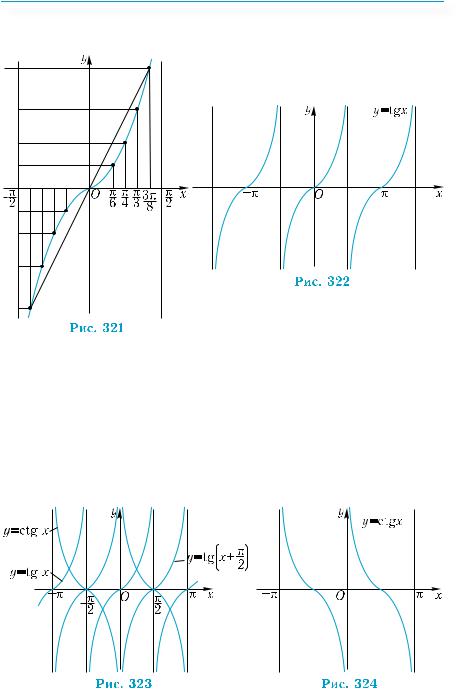
|
− |
π |
; |
π |
пре- |
|
На втором этапе построим график на промежутке |
2 |
2 |
|
|||
|
|
|
|
|
||
образованием симметрии, воспользовавшись нечётностью танген-
са (рис. 321).
Тем самим получили график функции у = tgx на промежутке, длина которого равна наименьшему положительному периоду π тангенса.
Так как функция у = tgx является периодической, то на третьем этапе ее полный график можно построить с помощью параллель-
292 |
Тригонометрические функции |
ного переноса полученного графика вдоль оси х на ±π; ±2π и т. д. (рис. 322). График функции у = tgx называют тангенсоидой.
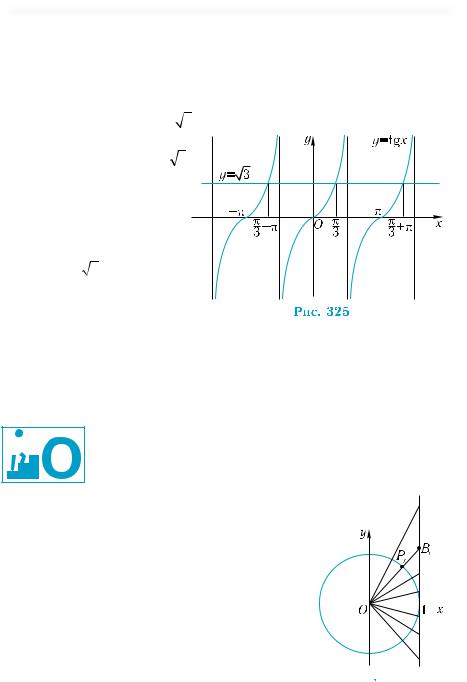
График функции у = ctg х можно получить из графика функции у = tg х. Для этого, в соответствии с формулой приведения
ctgx = −tg x + π2 , достаточно график функции у = tgx парал-
лельно перенести в отрицательном направлении оси х на π2 , а
затем отобразить полученный график симметрично относительно оси абсцисс. На рис 323 тангенсоида изображена тонкой
Свойства и графики тригонометрических функций |
293 |
линией, сдвинутая тангенсоида – штриховой, график функции
у = ctg х — жирной.
В окончательном виде график функции у = ctg х изображён на рис. 324.
Пример 8. Найти абсциссы точек пересечения графика функ-
ции у = tg х с прямой y = |
3 . |
Построив графики фун- |
|
кций у = tg х и y = |
3 |
(рис. 325), увидим, что та
ветвь графика тангенса, ко- |
|||||||
торая |
соответствует проме- |
||||||
жутку |
|
− |
π |
; |
π |
пересекает |
|
|
2 |
, |
|||||
|
|
|
|
2 |
|
||
прямую y = |
|
3 в точке с абс- |
|||||
циссой |
|
x0 |
= |
π . |
Остальные |
||
|
|
|
|
|
|
3 |
|
точки пересечения имеют аб-
сциссы х0 + π; х0 – π, х0 + 2π, х0 – 2π и т. д. Итак, x = 3π + πk,k Z.
Ответ: 3π + πk,k Z.
Свойство 6 монотонности функций у = tg х и у = ctg х 
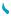 имеет простую геометрическую интерпретацию.
имеет простую геометрическую интерпретацию.
Если х возрастает от – π2 до π2 , то tg х, то есть коор-
дината точки Вх, являющейся точкой пересечения прямой OPx с линией тангенсов, воз-
растает от – ∞ до + ∞ (рис. 326). Иначе говоря,
если х = 0, то tg х = 0, а когда х приближается
кπ2 , оставаясь меньше π2 , tg х возрастает
иможет принимать какие угодно большие  значения.
значения.
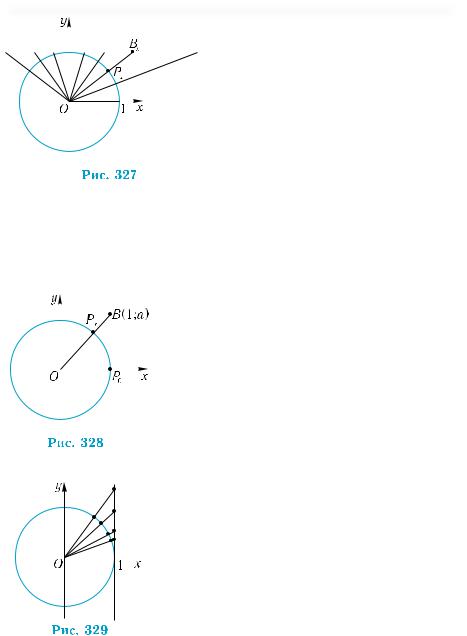
Аналогично, из геометрического смысла котангенса вытекает, что если х возрастает
от 0 до π, координата точки Сх на линии ко- 



294 |
|
|
|
Тригонометрические функции |
|
|
|
|
|
тангенсов, являющейся точкой пе- |
|
|
|
|
|||
|
|
|
|
ресечения прямой ОРх с линией |
|
|
|
|
|
котангенсов, равная сtg х, убывает |
|
|
|
|
|
||
|
|
|
|
от +∞ |
до – ∞ (рис. 327). Иначе гово- |
|
|
|
|
ря, если х = π , то сtg х = 0, а если х |
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
приближается к 0, оставаясь боль- |
|
|
|
|
|
ше 0, значения сtg х возрастают и |
|
|
|
|
|
могут |
принимать какие угодно |
|
|
|
|||
большие значения.
Обоснуем свойство 7 о множестве значений функций у = tg х и у = ctg х.
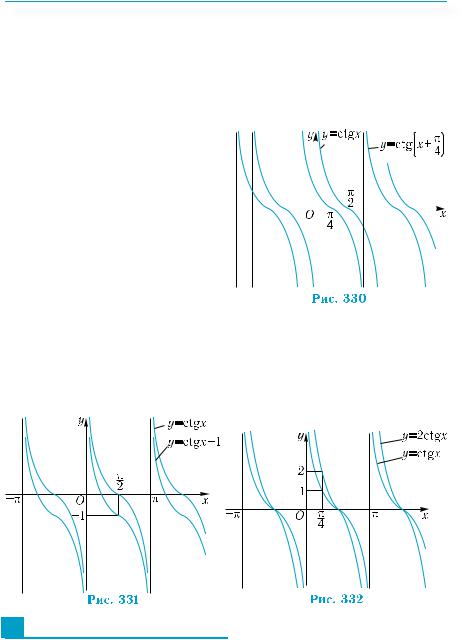
Докажем, что произвольное действительное число а может
быть значением тангенса некоторого числа. Рассмотрим тригоно-
метрическую окружность и проведем линию тангенсов (рис. 328), |
||||||||
|
|
|
обозначив на ней точку В(1; а). Соединим |
|||||
|
|
|
точки О и В и обозначим через Рх |
точку пе- |
||||
|
|
|
||||||
|
|
|
ресечения прямой ОВ с окружностью. Точ- |
|||||
|
|
|
ка Рх соответствует некоторому числу |
х, |
||||
|
|
|
принадлежащему промежутку |
|
π |
; |
π |
|
|
|
|
− |
2 |
2 |
, |
||
|
|
|
|
|
|
|
||
|
|
|
её координаты — (cos х; sin х). Поэтому |
|||||
|
|
|
Р0В = tg x = а. Аналогично свойство дока- |
|||||
|
|
|
зывается для у = ctg х. |
|
|
|
|
|
|
|
|
Свойство 8, то есть непрерывность фун- |
|||||
|
|
|
кции у = tg х, вытекает из того, что если |
|||||
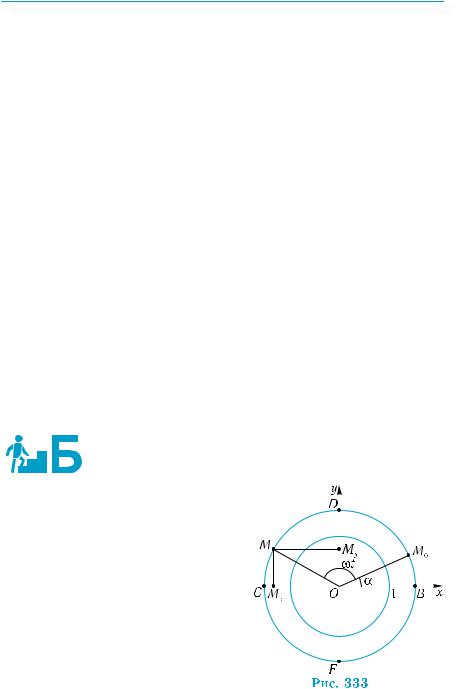
две точки на тригонометрическй окружности сближаются (расстояние между ними становится каким угодно малым), то соответствующие точки на линии тангенсов также сближаются (рис. 329). Аналогично
 обосновывается это свойство для функции у = сtg х. Напомним, что непрерывная функция описывает процессы, которые происходят плавно, то есть когда исследуемая величина за малый промежуток времени
обосновывается это свойство для функции у = сtg х. Напомним, что непрерывная функция описывает процессы, которые происходят плавно, то есть когда исследуемая величина за малый промежуток времени
изменяется мало (см. § 4).
Применим к графикам функций у = tg х и у = сtg х преобразования графиков функций, рассматривавшиеся ранее, а именно: па-
Свойства и графики тригонометрических функций |
295 |
раллельный перенос графика вдоль координатных осей, сжатие и растяжение графика, симметричное отображение относительно координатных осей.
Пример |
9. |
Построить графики функции: |
1) |
|
|
π |
; |
|||||||||
y = ctg x + |
|
|
||||||||||||||
2) y = ctg x – 1; 3) y = 2ctg x. |
|
|
|
|
|
|
|
|
|
4 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1) |
График |
функции |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
π |
можно |
получить |
|
|
|
|
|
|
|
|
|
|
||
y = ctg x + |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
из графика функции у = ctgx па- |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
раллельным |
переносом |
его |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
вдоль оси абсцисс в отрицатель- |
|
|
|
|
|
|
|
|
|
|
||||||
ном направлении оси х на |
π |
|
|
|
|
|
|
|
|
|
|
|||||
(рис. 330). |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) График функции у = ctg x – 1 |
параллельным пе- |
|||||||||||||||
можно получить из графика функции у = ctgx |
||||||||||||||||
реносом его вдоль оси ординат в отрицательном направлении оси
у на 1 (рис. 331).
3) График функции y = 2ctg x можна получить из графика функции у = ctg х растяжением его от оси абсцисс в два раза
(рис. 332).
Контрольные вопросы
1°. Имеет ли смысл запись: а) tg 2011; б) сtg 2011π?
2°. Является ли функция у = tg х возрастающей на промежутке:
296 |
Тригонометрические функции |
|
|
|
− |
π |
; |
|
π |
|
|
|
π |
; |
π |
|
в) [0; π]; |
|
г) (3; 3,1)? |
|||||||
|
|
a) |
6 |
6 |
; |
б) − |
4 |
3 |
; |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
3°. |
Справедливо ли неравенство ctg x < 0 во всех точках проме- |
|||||||||||||||||||||||
|
|
жутка: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2π |
; |
5π |
π |
; |
3π |
|
π |
; |
3π |
г) (2; 2,5)? |
|||||||||||
|
|
а) |
|
3 |
|
|
6 |
; |
б) |
2 |
|
|
; |
в) |
4 |
; |
||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
6 |
|
|
|
|
|||||||
4°. |
В каких точках функции у = tg х и у = ctg х равняются нулю? |
|||||||||||||||||||||||
5°. |
Какова область определения функции: |
в) ctg (х – 2); |
||||||||||||||||||||||
|
|
а) y |
= tg x |
+ 1; |
|
|
б) |
у = tg (х – 1); |
|
|
||||||||||||||
|
|
г) y |
= ctg x + 2; |
|
|
д) y |
= ctg 3x? |
|
|
принимать значения |
||||||||||||||
6. |
Могут ли функции у |
|
= tg х |
и у = ctg х |
||||||||||||||||||||
|
|
0,0000001; 2011; 10–20; 1020? |
|
|
|
|
|
|
|
|||||||||||||||
7. |
Каково множество значений функции: |
|
б) y = сtg x – 1? |
|||||||||||||||||||||
|
|
а) y |
= tg (x + 1); |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
8. |
Можно ли утверждать, что котангенс убывает: |
|||||||||||||||||||||||
|
|
а) на всей своей области определения; |
|
|
|
|||||||||||||||||||
|
|
б) на каждом интервале, который полностью лежит в его об- |
||||||||||||||||||||||
|
|
ласти определения? |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
9. |
Чему равен наименьший положительный период функции: |
|||||||||||||||||||||||
|
|
а) y = tg 2x; |
|
|
|
|
|
|
|
б) y = ctg x ? |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
4. Гармонические колебания |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
Пусть по окружности радиуса А движется точка с |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
постоянной угловой скоростью ω, то есть за единицу |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
времени точка поворачивается на угол ω рад. За t |
||||||||||||||
|
единиц времени эта точка повер- |
|
|
|
|
|
||||||||||||||||||
нется на угол ωt рад. В начальный |
|
|
|
|
|
|||||||||||||||||||
момент |
|
времени |
точка |
|
занимает |
|
|
|
|
|
||||||||||||||
положение |
M0, угол ВОМ0 |
равен α |
|
|
|
|
|
|||||||||||||||||
рад (рис. 333). В момент времени |
|
|
|
|
|
|||||||||||||||||||
t точка займёт положение M, угол |
|
|
|
|
|
|||||||||||||||||||
М0ОМ будет равным ωt |
|
рад, угол |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
ВОМ будет равным (ωt |
+ α) рад. |
|
|
|
|
|
|
|
||||||||||||||||
|
|
Обозначим через Мх |
и |
|
Му |
проек- |
|
|
|
|
|
|||||||||||||
ции точки |
М |
на оси х и |
у |
соответс- |
|
|
|
|
|
|||||||||||||||
твенно. Во время движения точки |
|
|
|
|
|
|||||||||||||||||||
М |
по окружности ее проекция |
Мх |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||||

Свойства и графики тригонометрических функций |
297 |
на ось х совершает колебания вдоль горизонтального диаметра ВС длиной 2А, достигая то крайнего правого положения В, то крайнего левого положения С. Точно так же и ее проекция Му на ось у совершает колебания вдоль вертикального диаметра DF, также достигая то наивысшего положения D, то самого нижнего положения F. Установим законы движения точек Мх и Му. Построим единичную окружность с центром в точке О и обозначим через Т точку пересечения луча ОМ с этой окружностью. Координаты точки Т = Рωt + α равны cos (ωt + α) и sin (ωt + α), а потому, из соображений подобия, координаты точки М определяются формулами:
х = A cos(ωt + α), у = A sin (ωt + α).
Эти формулы описывают отклонение точек Мх и Му от точки О — центра окружности. Они задают законы движения точек Мх
и Му, которые называются гармоническими колебаниями.
Отметим, что при А = 1, ω = 1, α = 0 получим соответственно функции x(t) = cos t, у(t) = sin t.
Колебательные движения широко распространены в окружающем мире. Представления о них дают и океанские волны, и маятниковые часы, и качели, и нервные импульсы. С ними связано распространение звука и света. Многие из этих явлений можно описать с помощью гармонических колебаний.
Введем некоторые понятия, связанные с гармоническими колебаниями проекций на координатные оси точки, равномерно движущейся по окружности с центром в начале координат. Точку О — середину отрезка, вдоль которого проходит гармоническое колебание, — называют положением равновесия, число А — амплитудой колебания. Амплитуда характеризует величину наибольшего отклонения от положения равновесия.
Число ω, как известно, является угловой скоростью вращения точки. За 2π единиц времени точка повернется на угол 2πω рад,
при этом ее проекции на ось х и на ось у выполнят 22πωπ = ω пол-
ных колебаний. Число ω, то есть количество полных колебаний за 2π единиц времени, называется еще круговой частотой коле-
баний.
Число α, характеризующее начальное положение точки на ок-
ружности, называется начальной фазой колебания, ωt + α — фазой колебания.

298 Тригонометрические функции
Время Т, в течение которого точка М совершает полный оборот,
называется периодом гармонического колебания. За период
Т проекция Мх точки М на ось х дважды пройдет все свои возможные положения и возвратится в начальное положение. Исключе-
ния составляют лишь предельные положения В и С (см. рис. 333), каждое из которых точка пройдет один раз.
Так как за 2π единиц времени координата точки совершает ω полных колебаний, то одно полное колебание она совершает за
2π |
единиц времени, то есть Т = 2π . |
|||||
ω |
|
|
|
|
ω |
|
|
Величина, обратная периоду колебания, |
|||||
|
|
1 |
= |
ω |
, |
|
|
|
T |
|
|||
|
|
|
2π |
|||
называетсячастотойколебания.Онапоказывает,сколькополных |
||||||
колебаний совершает координата точки за единицу времени. |
||||||
|
|
Графикзаконагармоническогоколебания у=Asin(ωt + |
||||
|
|
|||||
|
|
|
α |
|||
|
|
+ α) = Asin ω t + |
можно построить из графика |
|||
|
|
|
ω |
|||
|
|
функции у(t)= sin t параллельным переносом вдоль |
||||
|
|
|||||
оси абсцисс на |
|
α |
|
единиц в положительном направлении оси, |
|
|
|||
|
|
ω |
|
|
если α < 0, и в отрицательном, если α > 0; растяжением от оси |
||||||
ω |
|
|
|
ω |
||
ординат в |
1 |
раз при 0 < ω < 1 или сжатием к оси ординат в ω раз |
||||
ω |
||||||
|
|
|
|
|
||
при ω > 1; растяжением от оси абсцисс в А раз, если А > 1, или |
||||||
сжатием к оси абсцисс в |
1 |
|
раз, если 0 < A < 1. |
|||
A |
||||||
Функцию |
|
+ α) можно получить из функции |
||||
x = A cos(ωt |
||||||
у = Asin(ωt + α) , заменив α на α + π . |
||||||
|
|
|
|
|
2 |
|
Пример 10. Построить график закона гармонического колебания
y= 5sin 2t + π .
3
Представим выражение для закона гармонического колеба-
ния в виде: |
|
2t + |
π |
= 5sin 2 |
|
π |
График строим в та- |
||
y = 5sin |
3 |
|
t + |
6 |
. |
||||
|
|
|
|
|
|
|
|
||

Свойства и графики тригонометрических функций |
299 |
кой последовательности: сначала строим график функции у = sin t
|
π |
|
|
|
|
(рис. 334), далее y = sin t + |
(параллельным переносом преды- |
||||
|
6 |
|
|
|
|
дущего графика вдоль оси абсцисс на |
π |
единиц в отрицательном |
|||
|
|
6 |
|
π |
|
направлении оси) (см. рис. 334), затем |
|||||
y = sin2 t + |
(сжатием |
||||
|
|
|
|
6 |
|
предыдущего графика к оси ординат в два раза) (рис. 335) и, нако-

300 |
|
|
|
Тригонометрические функции |
нец, |
|
2t + |
π |
(растяжением предыдущего графика от оси |
y = 5sin |
|
|||
|
|
|
3 |
|
абсцисс в 5 раз) (рис. 336). |
||||
|
Контрольные вопросы |
|
1°. |
Чему равна амплитуда гармонического колебания проекции |
|
|
на ось х точки, равномерно движущейся по окружности диа- |
|
|
метра 10 см с центром в начале координат? |
|
2°. |
Чему равна круговая частота гармонического колебания про- |
|
|
екции на ось у точки, равномерно движущейся с угловой ско- |
|
|
ростью 5 рад/с по окружности с центром в начале координат? |
|
3°. |
Чему равен период гармонического колебания проекции на |
|
|
ось х точки, равномерно движущейся с угловой скоростью |
|
|
5 рад/с по окружности с центром в начале координат? |
|
4°. |
Чему равна угловая скорость равномерного движения точки |
|
|
по окружности, если период соответствующего гармоническо- |
|
|
го колебания координат равен 4? |
|
5. |
Чему равна линейная скорость равномерного движения точ- |
|
|
ки по окружности радиуса 2, если период соответствующего |
|
|
гармонического колебания координат равен 4? |
|
6. |
Известно, что проекция точки, равномерно движущейся по |
|
|
окружности, на вертикальный диаметр совершает гармони- |
|
|
|
π |
|
ческое колебание, определяемое формулой y = 3sin 5t − |
. |
|
|
6 |
|
По какому закону изменяется проекция этой точки на гори- |
|
|
зонтальный диаметр? |
|
7°. |
Чему равна начальная фаза гармонического колебания про- |
|
|
екции на ось у точки, равномерно движущейся по окружности |
|
|
с центром в начале координат, если в начальный момент вре- |
|
|
мени её положение совпадает с верхним концом вертикально- |
|
|
го диаметра? |
|
Задачи
281°. Вычислите: |
|
|
|
|
|
|
||
1) cos |
17π |
; |
2) tg 3360°; 3) |
|
− |
123π |
; 4) ctg (–1950°). |
|
3 |
sin |
4 |
|
|||||
|
|
|
|
|
|
|
||
Свойства и графики тригонометрических функций |
|
|
|
|
|
|
301 |
||||
282°. Упростите: |
2) |
|
|
|
|
|
|
|
|
|
|
1) |
sin2 (α + 4π) + cos2 (α + 6π); |
|
tg(α +3π) ctg(α −5π); |
|
|||||||
3) |
1+ ctg2 (α −7π); |
4) |
|
|
1 |
|
|
−1. |
|
|
|
|
cos2 (2α −8π) |
|
|
||||||||
283°. Докажите равенство: |
|
|
|
|
|
|
|||||
|
|
|
|
π |
|
|
|
2π |
|||
1) cos (t – π) = cos (t + π); |
2) |
|
|
2t − |
|
|
2t + |
||||
tg |
|
= tg |
3 |
. |
|||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
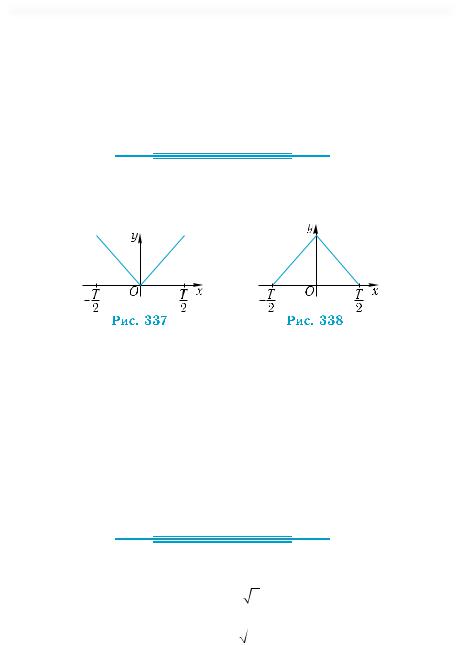
284.На рис. 337, 338 изображены части графиков функций с периодом Т. Постройте графики этих функций на промежутке
[–2Т; 2Т].
285.Докажите, що число Т является периодом функции y = f(x), если:
|
1) |
f(x) = cosx |
,T = 4π; |
2) f(x) = sin2x,T = π; |
|||
|
3) |
2 |
|
|
|
|
|
|
f(x) = ctgπx,T =1 . |
|
|
|
|
||
286. |
Докажите, что функция f является периодической, если: |
||||||
|
1) f(x) = 1 + cos x; |
2) f(x) = ctg 2x. |
|||||
287. |
Найдите наименьший положительный период, если он су- |
||||||
|
ществует, для функции: |
|
3x |
|
|
||
|
1) |
y = 2sin x ; |
2) y = 3ctg |
|
; |
3) y = sin2 x + cos2 x . |
|
|
2 |
||||||
|
|
3 |
|
|
|
||
288.Постройте график функции y = sinx, x [−π;2π] и укажите на нём точки, для которых:
1°) sin х = 1; |
2°) sin x = |
3 |
; |
3°) sin x = |
1 |
; |
||
2 |
|
3 |
||||||
|
|
|
|
|
|
|
||
4) sin х < 0; |
5) sin х > |
|
2 |
|
; |
6)sin х < − |
1 . |
|
|
2 |
|
||||||
|
|
|
|
|
|
2 |
|
|

302 |
Тригонометрические функции |
289.Постройте график функции y = cosx, x [−2π; π] и укажите на нём точки, для которых:
1°) cos х = – 1; |
|
2°) cos х = – |
|
2 |
; |
|
3°) cos х = |
2 ; |
|
||||||||||||
|
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
||||
4) cos х > 0; |
|
5) cos x < 1 |
; |
|
|
|
6) cosx > − |
|
2 |
||||||||||||
|
|
|
|
2 |
|
||||||||||||||||
290. Решите уравнение: |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1) sin x = |
2 x ; |
|
|
|
2) cos x = – 2 x + 1. |
|
|
|
|
||||||||||||
|
|
|
π |
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
||
291. Найдите область определения функции: |
|
|
|
|
|
|
|||||||||||||||
1°) |
y = 2sin x −3 |
; |
2°) |
y = |
1 |
|
|
; |
3) |
y = |
|
1 |
|
|
|||||||
cos2 x +3 |
sin x −1 |
||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||
4) |
y = |
1 |
|
; |
|
5*) |
y = |
sin x ; |
|
|
|
6*) |
y = |
|
1 |
|
|||||
cos x |
|
|
|
|
cos x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
.
;
.
292.Какие из функций являются чётными, какие — нечётными, а какие — ни чётными, ни нечётными:
1) |
y = sin |
2 |
x |
; |
|
2) |
y = |
1 |
+ cos x |
; |
|
3) |
y = x + sin x |
; |
|||
|
|
|
|
|
|
|
|
x2 |
|
|
|
||||||
4) |
y = |
sin x |
|
|
; |
5) |
y = |
|
1 − cos x |
|
; |
6) |
y =1 + sin x ? |
||||
cos2 x |
|
|
1 |
−sin2 x |
|||||||||||||
293. Разбейте данный отрезок на два промежутка так, чтобы на |
|||||||||||||||||
одном из них функция у = sin x убывала, а на втором — воз- |
|||||||||||||||||
растала: |
|
|
|
|
|
|
−π; π ; |
|
|
3) − π; 3π . |
|
||||||
1) |
π;2π ; |
|
|
|
2) |
|
|
|
|||||||||
2 2 2 2
294.Разбейте данный отрезок на два промежутка так, чтобы на одном из них функция у = cos х принимала неотрицательные значения, а на втором — неположительные:
1) [0; π ]; |
2) |
|
− |
π |
; |
3π |
; |
3) |
π |
|
||
|
2 |
2 |
|
|
2 |
;2π . |
||||||
|
|
|
|
|
|
|
|
|
|
|||
295. Найдите промежутки возрастания и убывания функции: |
|||||||||||||
1°) y = 2cos x; |
|
π |
|
|
|
2°) y = sin x – 3; |
π |
|
|||||
3) |
|
|
|
|
|
4) |
y =1 |
|
2x + |
; |
|||
y = 2cos 3x − |
4 |
; |
|
|
− sin |
3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
5) |
|
2x − |
π |
; |
6) |
y =1 |
|
2x − |
π |
|
|||
y = 0,5sin |
6 |
|
+ cos |
3 |
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||

Свойства и графики тригонометрических функций |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
303 |
||||||||||||||
296. |
Сравните числа: |
|
|
2°) sin 220° и sin 260°; |
|
|
|
|
|
|
|||||||||||||||||||||
|
1°) sin 37° и sin 86°; |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
π |
|
|
|
|
|||
|
3°) cos 200° и cos 230°; |
|
4) sin |
− |
|
|
и sin |
− |
|
|
|
|
|
; |
|
|
|
||||||||||||||
|
|
|
10 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
4π |
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
− |
π |
|
|
; |
6) sin(–3) и sin(–2); |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
5*) cos |
7 |
и sin |
7 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
||||||||
|
7) cos |
π |
|
и sin |
π |
; |
|
|
|
|
|
π |
|
и sin |
. |
|
|
|
|
||||||||||||
|
7 |
|
7 |
|
|
8*) cos − |
8 |
|
8 |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
297. Найдите множество значений функции: |
|
– 1; 4) у = cos2х; |
|||||||||||||||||||||||||||||
|
1°) у = sin 3x; |
2°) |
у = 3sin х; |
3°) y = 3cos x |
|||||||||||||||||||||||||||
|
5) у = |
1 |
sin |
2 |
x −1 ; |
|
|
|
π |
; 7) y = |
3cos2x |
− |
π |
. |
|
||||||||||||||||
|
2 |
|
|
6) y = 3sin 2x − |
|
6 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
298. |
Постройте график функции: |
2°) y = sin3x; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
l°) y = 2cosx; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
3) y = cos |
x |
|
−1 |
; |
|
|
|
|
|
|
|
x |
− |
π |
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
4*) y = 3sin |
3 |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
299*. Постройте график зависимости моментов заката Солнца на |
|||||||||||||||||||||||||||||||
|
первое число месяца в зависимости от месяца, взяв за на- |
||||||||||||||||||||||||||||||
|
чало оси ординат среднее время заката Солнца — 18 часов, |
||||||||||||||||||||||||||||||
|
соедините полученные точки плавной непрерывной линией |
||||||||||||||||||||||||||||||
|
(эти данные можно взять из отрывных календарей за раз- |
||||||||||||||||||||||||||||||
|
ные годы или найти в Интернете). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1) Является ли эта зависимость функциональной? |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
2) График какой функции вам напоминает построенный |
||||||||||||||||||||||||||||||
|
график? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
3) Чем вы объясняете такое сходство? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
4) Как можно уточнить построенный график? |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
5) Чем вы объясняете отличия построенного графика от гра- |
||||||||||||||||||||||||||||||
|
фика известной вам функции? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
6) Предложите содержательную интерпретацию области |
||||||||||||||||||||||||||||||
|
определения, множества значений, промежутков монотон- |
||||||||||||||||||||||||||||||
|
ности, нулей, наибольшего и наименьшего значений, пери- |
||||||||||||||||||||||||||||||
|
одичности функции, график которой построен. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
300. |
Найдите область определения функции: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
1°) y = tg3x; |
|
2°) |
|
|
π |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||||
|
|
y = tg x + |
; 3) y = |
|
|
|
|
|
; |
4) y = |
|
|
|
|
|
. |
|||||||||||||||
|
|
|
ctgx |
|
tgx |
+1 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||||||

304 |
Тригонометрические функции |
301.Какие из функций являются чётными, какие нечётными, а какие — ни чётными, ни нечётными:
1°) y = tgx cos2x; 2°) y = tg x + ctg x ; 3°) у = tg 2x sin х;
4°) |
y = sin x + tgx |
; 5) y = ctgx + cosx; |
6) y = x + sin x |
? |
||||||||||||
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
tg3x |
|
|
302. Сравните числа: |
|
|
2) tg π |
|
4π |
|
|
|
|
|
||||||
1) tg (–80°) и tg (–50°); |
и tg |
|
; |
|
|
|
||||||||||
|
|
|
|
|||||||||||||
3) tg 1 и tg l,6; |
|
|
|
5 |
5 |
|
|
|
|
|
||||||
|
|
|
4) tg (–2) и tg (–3); |
|
|
|||||||||||
|
|
− |
π |
|
и ctg |
π |
; |
6) ctg 95° и ctg 117°; |
|
|||||||
5) ctg |
8 |
|
9 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
7) ctg 2 и ctg 3; |
|
|
8) tg π |
и ctg π . |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
6 |
4 |
|
|
|
|
|
|
303. Укажите промежутки возрастания и убывания функции: |
||||||||||||||||
1°) y = ctg 2x; |
|
|
2°) y = ctg x – 1; |
3) y = 2tg x; |
|
|||||||||||
4) |
|
|
+ |
π |
|
|
5*) у = tg2 x; |
6*) y = ctg2 x; |
|
|||||||
y = tg x |
4 |
; |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
7*) |
|
|
x |
− |
π |
|
|
|
|
x |
+ |
π |
|
|||
y = tg |
2 |
; |
|
|
8*) y = 2 + ctg |
3 |
. |
|
||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|||
304. Найдите множество значений функции: |
|
|
|
|
||||||||||||
1°) y = tg(x + 1); |
|
|
2°) y = сtgx – 1; |
|
|
|
||||||||||
3) y = ctgx,0 < x < π; |
4) y = tg2x ; |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
4 |
y = ctg3x ; |
7) y = −ctg2x . |
|
||||||
5) y = tg x ctg x; |
|
6) |
|
|||||||||||||
305. Укажите наибольшее и наименьшее значения функции:
1°) y = tgx, −4π ≤ x ≤ 4π;
3)y = sinx + tgx, 0 ≤ x ≤ 4π.
306.Постройте график функции: 1°) y = tgx, x −3π;− π ;
2 2
3°) у = ctgx – l;
5) y = tg x2 ;
2) y = ctg 2x , 3π ≤ x ≤ 23π;
2°) y = ctgx, x (−π; 0);
4°) |
|
π |
|
|
|
y = tg x + |
; |
|
|
|
|
|
|
6 |
π , |
|
|
|
tgx при x ≤ |
|
|||
|
|
|
4 |
|
|
6*) y = |
|
|
π |
|
|
|
|
|
|
. |
|
|
ctgx при x > |
4 |
|||
|
|
|
|
|
|

Свойства и графики тригонометрических функций |
305 |
307°. Найдите амплитуду, период и начальную фазу закона гар- |
|||||||||
монического колебания, заданного формулой: |
|
|
|||||||
|
π |
|
1 |
|
π |
t |
|
|
|
l) y = 3sin 2t + |
; |
2) y = |
2 |
sin πt + |
;3) |
y = 2sin |
|
+1 |
; |
|
|||||||||
|
3 |
|
|
4 |
2 |
|
|
||
4) у = 3 sin 4t; |
|
5) y = sin (t – 1). |
|
|
|
|
|
||
308°. Дан закон, по которому изменяется координата (измеряе-
мая в сантиметрах) движущегося тела. Найдите амплитуду,
период, круговую частоту колебания. Вычислите координа- |
|||
ту тела в момент времени t0, если: |
|||
1) x(t) = 2,5cos3πt,t = 1 c; |
|||
|
0 |
9 |
|
2) x(t) = 7cos 4πt + |
π |
||
,t = 2,5 c; |
|||
|
|
0 |
|
|
4 |
|
|
3) x(t) = 2cos2πt,t0 = 0,25 c;
4) x(t) =1,5cos πt + π ,t = 3,5 c.
3 6 0
309.Данзакон,покоторомуизменяетсясовременемсилапеременного тока: I(t) = 5sin10πt, I — сила тока, A; t — время, с.
1°) Найдите амплитуду, период, круговую частоту колебаний силы тока.
2°) Чему равна сила тока в момент времени t = 0,05 c?
3)В какие моменты времени сила тока принимает наибольшее значение?
310.Дан закон, по которому изменяется со временем напряжение:U(t) = 220 cos60πt, U — напряжение, В; t — время, с. 1°) Найдите амплитуду, период, частоту колебаний напряжения.
2°) Чему равняется напряжение в момент времени t = 0,5 c?
3)В какие моменты времени напряжение принимает наибольшее значение?
Точка выполняет гармоническое колебание по закону:
y= 2sin 3t − π .
2
1) Найдите амплитуду, период и начальную фазу этого колебания.

306 |
Тригонометрические функции |
2)Укажите, какие преобразования следует выполнить над синусоидой у = sin t, чтобы получить график данного колебания.
3)Постройте схематически график гармонического колебания.
312.Ордината точки, вращающейся по окружности, совершает
гармоническое колебание по закону: |
|
3t − |
π |
Най- |
|
y = 2sin |
2 |
. |
|||
|
|
|
|
|
|
дите моменты времени, в которых точка расположена в одном из крайних положений:
1)верхнем; 2) левом; 3) нижнем; 4) правом.
313.Напишите закон гармонического колебания, если:
1)амплитуда равна 1, период 0,2 с, начальная фаза 6π;
2)за 1 мин совершается 180 колебаний с амплитудой 7 см, а начальная фаза колебаний равна π2 .
Упражнения для повторения
314.Какой знак имеет скалярное произведение векторов, если угол между ними: 1) острый; 2) тупой? Справедливы ли обратные утверждения?
315.Вычислите скалярное произведение векторов a и b , если
|
a |
|
= 2, |
|
b |
|
= 3 и угол между ними равен: 1) 60°; 2) 135°; 3) 90°; |
|||||||||
|
|
|
|
|||||||||||||
|
|
|||||||||||||||
4) |
0°; 5) 180°. |
|
|
|
|
|
|
|
|
|
||||||
316. Чему равняется скалярное произведение векторов: |
|
|
|
|||||||||||||
1) |
|
(а; 0) и (b; 0); |
2) (а; 0) и (0; b); |
|
|
|
|
|
|
|||||||
3) (а; b) и (a; b); |
4) (а; b) и (– a; – b)? |
|
|
|
|
|||||||||||
317. Даны векторы a = (1; 2),b = (−2; 3). Вычислите: |
|
|
|
|
|
|||||||||||
1) |
|
2a · b ; |
2) a · (–3b ); |
|
− |
1 |
|
1 |
|
; |
||||||
|
3) |
2 |
a |
|
3 |
b |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4) b · (a + b ); |
5) (a + b )2; |
6) (a – b )2; |
|
|
|
|||||||||||
7) (a + b ) · (a – b ). |
|
|
|
|
|
|
|
|
||||||||
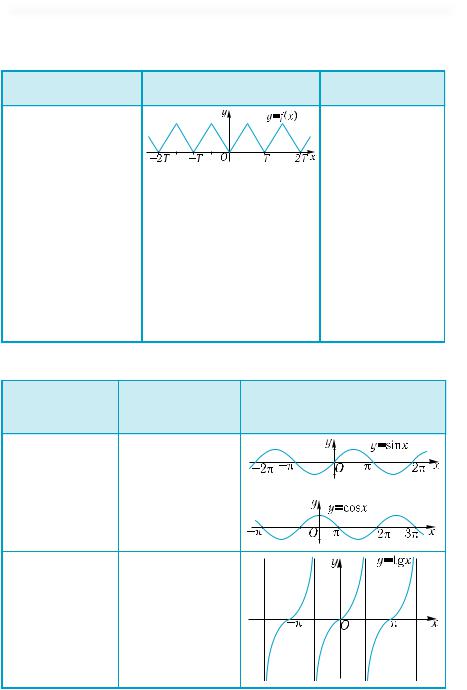
Свойства и графики тригонометрических функций |
|
307 |
|||
|
|
|
Итог |
|
|
|
|
|
Основное понятие |
|
|
Определение |
Геометрическая |
Применение |
|||
|
|
|
иллюстрация |
|
|
Функция у = f(х) |
Периодические |
||||
называется |
пери- |
функции |
описы- |
||
одической, |
если |
вают различные |
|||
существует |
такое |
ситуации |
(аст- |
||
число T ≠ 0, что об- |
рономические |
||||
ласть определения |
явления, |
жизне- |
|||
функции |
вместе |
с |
деятельность ор- |
||
каждой точкой х со- |
ганизма и т. п.), |
||||
держит точки х ± Т |
периодически |
||||
и при этом выпол- |
повторяющиеся. |
||||
няется |
равенство |
|
|
||
f(х ± Т) = f(x). Число |
|
|
|||
Т называется пери- |
|
|
|||
одом функции. |
|
|
|
||
Словесная
формулировка
Функцииу=sinх
и у = cos х — пе-
риодические с наименьшим положительным периодом 2π.
Функция у = = tg х периодичнаснаименьшим положительным периодомπ.
Основные утверждения
Запись с помо- |
Графическая иллюстрация, |
|
щью формул, |
комментарии, пояснения |
|
пояснения |
||
|
sin(x + 2π) = sin x cos(x + 2π) = cos x
tg(x + π) = tgx
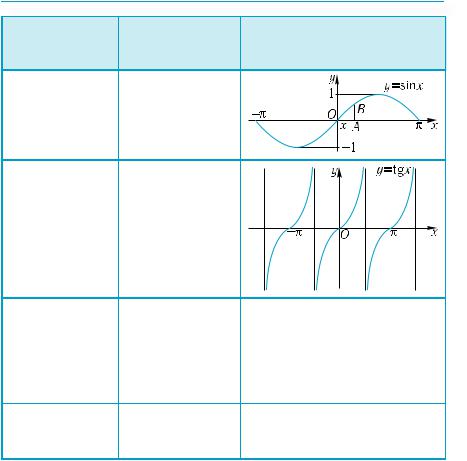
308
Словесная
формулировка
Множеством значений функций у = sin х и у = cos х являет- сяотрезок[–1;1].
Множеством значений функции у = tg х является множество всех действительных чисел.
|
Тригонометрические функции |
|
Запись с помо- |
Графическая иллюстрация, |
|
щью формул, |
комментарии, пояснения |
|
пояснения |
||
|
E(y) = [–1; 1]
Е(у) = R
Функция |
у |
= |
sin (–х) = –sin х, |
График функции у = sin х |
= sin х — нечёт- |
cos(–х) = cosх |
симметричен относительно |
||
ная, а функция |
|
начала координат, график |
||
у = cos х |
— чёт- |
|
функции у = cos х симметри- |
|
ная. |
|
|
|
чен относительно оси орди- |
|
|
|
|
нат |
Функция |
у |
= |
tg (–х) = –tg х |
График функции у = tg х сим- |
= tg х — нечёт- |
|
метричен относительно нача- |
||
ная. |
|
|
|
ла координат. |
