
- •Обращение к читателю
- •Введение
- •РАЗДЕЛ 1. Функции, их свойства и графики
- •§1. Числовые множества
- •§2. Вычисления и расчёты
- •§3. Функциональные зависимости
- •§4. Основные свойства функций
- •§5. Корни n-ой степени
- •§6. Степенные функции с рациональными показателями
- •§7. Основные понятия и аксиомы стереометрии
- •§8. Взаимное расположение двух прямых в пространстве
- •§9. Параллельное проектирование
- •§10. Изображение фигур в стереометрии
- •§11. Параллельность прямых и плоскостей
- •§12. Параллельность плоскостей
- •§13. Тригонометрические функции числового аргумента
- •§14. Основные соотношения между тригонометрическими функциями
- •§15. Свойства и графики тригонометрических функций
- •§16. Тригонометрические формулы сложения и следствия из них
- •§17. Простейшие тригонометрические уравнения и неравенства
- •§18. Перпендикулярность прямой и плоскости
- •§19. Связь между параллельностью и перпендикулярностью прямых и плоскостей
- •§20. Перпендикулярность плоскостей
- •§21. Ортогональное проектирование
- •§23. Измерение расстояний в пространстве
- •§24. Измерение углов в пространстве
- •Ответы и указания к задачам
- •Предметный указатель
- •Содержание

§13. Тригонометрические функции числового аргумента
В этом параграфе будут определены тригонометрические функции для произвольного числового аргумента. ×асто поло жение подвижных обúектов, например, небесных тел, опреде ляют с помощью углов, в частности, углов вращения. Поэтому функции, описывающие их движение, нередко своим аргумен том имеют меру угла. Следовательно, целесообразно обобщить понятие угла и подробнее обсудить вопрос о его измерении.
1. Радианное измерение углов
Известно, что в планиметрии рассматривают углы, 
 градусная мера которых находится в промежутке от
градусная мера которых находится в промежутке от  0° до 180°. Но на практике приходится рассматривать углы, мера которых больше 180°.
0° до 180°. Но на практике приходится рассматривать углы, мера которых больше 180°.
Например, самолет из пункта А должен перелететь в пункт В. Курс самолета определяют с помощью угла между направлением линии полета
и направлением меридиана «юг — север», который отсчитывают против движения часовой стрелки (рис. 262).
Следовательно,прирешениитаких задач приходится уже рассматривать углы в промежутке от 0° до 360°.
В геометрии углы рассматриваются как фигуры, образованные с помощью двух лучей, имеющих
общее начало. Лучи называются сторонами угла, их общая точка — вершиной угла.
Теперь, рассматривая угол, покажем, как эта фигура образовалась: один из лучей будем рассматривать как неподвижный, а второй луч — как движущийся от начального положения, в котором

236 Тригонометрические функции
он совмещался с неподвижной стороной. Эту вторую сторону мы
будем называть подвижной и будем считать, что угол образуется
вращением подвижного луча вокруг вершины угла. Полученные
при этом углы называют углами вращения. На рис. 263 изображен угол, образованный вращением подвижного луча ОА1 вокруг точки О, с неподвижным лучом ОА. Траекторией движения точки А1 луча ОА1 является линия АА1. Она является дугой окружности с центром в точке О и с радиусом ОА1 (или ОА). Следовательно, точка движется по дуге окружности
радиуса R = ОА.
Обычно углы в геометрии измеряют в градусах: 1 градус (1°) —
это |
1 |
часть меры прямого угла, или |
|
1 |
часть меры развернуто- |
|
90 |
180 |
|||||
|
|
|
||||
го угла. Углы вращения тоже можно измерять в градусах. Но часто более удобной является другая мера.
При вращении фиксированная точка подвижного луча описывает дугу окружности с центром в вершине угла (рис. 264). Измерение
углов вращения можно заменить измерением длины дуги окружности. Чтобы исключить влияние величины радиуса, мерой угла считают не длину дуги l, а отношение этой длины к радиусу R. Такая мера называется радианной.
!Отношение пути, пройденного точкой А, к радиусу R не зависит от радиуса. Поэтому это отношение может быть принято за меру угла вращения.
Радианной мерой угла вращения называется отношение пути, пройденного от начального положения фиксированной точкой подвижного луча, к расстоянию от этой точки до начала луча.
Численно радианная мера угла вращения равняется пути, пройденному точкой подвижного луча, находящейся на единичном расстоянии от вершины.
За единицу при радианном измерении угла вращения принимают меру угла, опирающего-
Тригонометрические функции числового аргумента |
237 |
ся на дугу, длина которой равна длине радиуса (рис. 265). Эта единица называется радианом.
Термин «радиан» происходит от латинского radius — радиус.
Движение точки по окружности во многом похоже на движение точки по прямой. Чтобы определить положение точки на прямой, недостаточно знать путь, пройденный ею от исходной точки, — нужно указать еще направление движения. Обычно на прямой фиксируют положительное направление, а положение точки определяется одним числом, положительным или отрицательным.
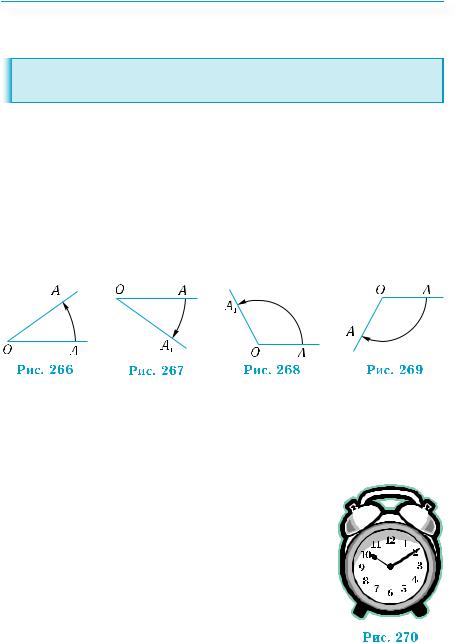
Вращение подвижного луча вокруг вершины угла возможно в двух противоположных направлениях. Геометрически два угла на рис. 266–267 являются равными, но как углы вращения их следует считать различными.
При вращении на плоскости будем считать положительным направлением вращения направление против движения часовой стрелки (рис. 268). Вращение по часовой стрелке будем считать отрицательным (рис. 269). Соответственно, углы, образованные такими вращениями, будем измерять положительными и отрицательными числами.
Например, часы на рис. 270 показывают 10 минут одиннадцатого, или без 50 минут один-
надцать часов. Здесь вращение минутной стрелки измеряется или отрицательным числом (по часовой стрелке), или положительным, только выбор направления мы обозначаем не знаком минус или плюс, а словами «10 минут одиннадцатого» и «без 50 минут одиннадцать».
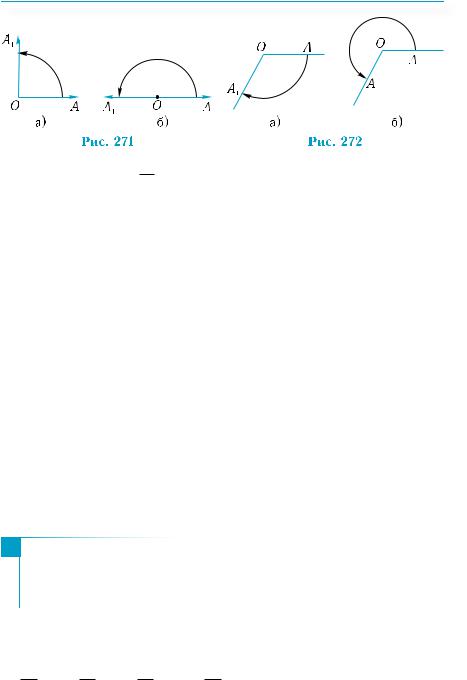
Угол в 90° получим, если луч ОА1 совершит четверть полного оборота вокруг точки О против
часовой стрелки (рис. 271, а); результатом полуоборота луча ОА1 против часовой стрелки является угол 180° (рис. 271, б). Угол
238 |
Тригонометрические функции |
(–150°) — это 150360 = 125 полного оборота луча ОА1 вокруг точки О по часовой стрелке (рис. 272, а).
Углы вращения обладают важной особенностью: их угловые
меры могут превышать 180°. Подвижный луч с началом в фик-
сированной точке может находиться в любом положении на плоскости (рис. 272, б).
Если угловая мера угла составляет α радиан, 0 < α < 2π, то это
означает, что длина соответствующей дуги окружности l радиуса
R равна αR, то есть l = αR.
Отсюда вытекает, что длина дуги единичной окружности
численно совпадает с радианной мерой соотвествующего
центрального угла. Собственно, именно это обстоятельство и делает радианную меру угла удобной.
Окружность радиуса R имеет длину 2πR . Рассмотрим дугу, длина которой равна радиусу R. Её длина в 2π раз меньше длины ок-
ружности. Поэтому угол, равный 1 радиану (сокращенно: рад), сос-
тавляет |
1 |
частиполногооборота:1рад= |
360° |
= |
180° |
≈ 57°17′45′′. |
||||||
|
2π |
π |
||||||||||
|
2π |
|
|
|
|
|
рад, то 1° |
|||||
Поскольку радианная мера угла 360° составляет 2π |
||||||||||||
соответствует |
2π |
= |
|
π |
≈ 0,017 рад. |
|
|
|
|
|
||
|
180 |
|
|
|
|
|
||||||
360 |
|
|
|
|
|
|
|
|||||
!Этим самым установлена связь между радианной и градусной мерами угла, которая, кстати, свидетельствует о независимости радианной меры угла от выбора фиксированной точки подвижного луча.
Пример 1. Выразить углы:
1) 30°, 45°, 60°, –150° в радианной мере; 2) 23π рад; 34π рад; 56π рад; − 43π рад в градусной мере.

Тригонометрические функции числового аргумента |
239 |
|
|
1) Поскольку 1° = |
|
π |
|
рад, |
то 30° = |
|
π |
|
30 = |
π |
рад; |
45° = |
||||||||||||||||
|
180 |
|
180 |
6 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= |
|
π |
|
45 = π |
рад; |
60° = |
|
π |
|
60 = |
π |
|
рад; |
−150° = |
|
|
π |
(−150) = |
||||||||||||
180 |
|
180 |
3 |
|
180 |
|||||||||||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= − |
5π |
рад. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 180° |
|
2π |
|
|
|
|
|
|
|
||||
|
|
2) Поскольку 1 рад = 180° , то |
2π |
|
рад |
|
=120°; |
3π |
рад = |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
3 |
|
|
|
|
π |
|
3 |
|
|
|
|
|
4 |
|
|
= |
|
180° 3π =135° ; |
5π |
|
рад |
|
|
= 180° |
|
5π =150° ; |
|
− 4π |
рад = |
|||||||||||||||||
|
|
|
π |
4 |
|
6 |
|
|
|
|
|
|
|
|
|
π |
|
6 |
|
|
|
|
|
|
|
|
3 |
|
|
|
=180° − 4π = −240° .
π3
Ответ:а) 6π рад; 4π рад; 3π рад; − 56π рад;б)120°,135°,150°,–240°.
Слово «радиан» часто опускают и говорят «угол». Так, записи α = 1,12; α = 0,39; α = 15,7 означают, что угол α измерен в радианах. В то же время обозначения градусов не принято опускать в записях.
Радианной мерой дуги окружности обычно называ- 
 ют радианную меру соответствующего центрально-
ют радианную меру соответствующего центрально-  го угла. Так, радианные меры дуг АА1, изображен-
го угла. Так, радианные меры дуг АА1, изображен-
ных на рис. 271 а), б) соответственно равны π2 , π .
Радианная мера единичной окружности равна её длине, то есть числу 2π, радианная мера единичной полуокружности равна числу π; радианная мера четверти единичной окружности состав-
ляет π2 .
Введение радианной меры угла вращения дает возможность установить простую связь между угловой и линейной скоростями движения точки, равномерно вращающейся вокруг некоторого центра. Угловая скорость при равномерном вращении — это мера угла, на который поворачивается точка за единицу времени. Она обычно измеряется в радианах за секунду (рад/с). Линейная скорость точки при равномерном движении — это расстояние, на которое перемещается точка по траектории движения за единицу времени.

240 |
Тригонометрические функции |
Пример 2. Точка равномерно движется по окружности, радиус которой R = 40 см, с линейной скоростью v = 80 см/с. Найти угловую скорость точки.
За одну секунду точка проходит путь, равный 80 см. Нужно найти меру угла, на который поворачивается точка за 1 с. Из определения радиана вытекает, что углу в 1 рад соответствует дуга, длина которой равна длине радиуса. Поскольку длина пути, который проходит точка за 1 с, вдвое больше радиуса, то соответствующая дуга окружности соответствует углу в 2 рад.
Ответ. 2 рад/с.
Используя отрицательные меры углов, можно модуль меры
любого угла, в пределах полного оборота, привести к числу, не
превышающему полуоборота. Например, при градусном измере-
нии углов вместо промежутка 0° ≤ α ≤ 360° можно всегда рассмат-
ривать углы в промежутке – 180° ≤ α ≤ 180°, при радианном изме-
рении вместо промежутка 0 ≤ α ≤ 2π — рассматривать промежуток |
|||||||
−π ≤ α ≤ π . Так, вместо угла 225° можно рассматривать |
угол |
||||||
–(360° – 225°) = –135°; вместо угла |
5π |
|
2π − |
5π |
= − |
π |
. |
3 |
— угол – |
|
3 |
||||
|
|
|
3 |
|
|
||
В географии, астрономии, где применяется градусная система измерения углов, пользуются также меньшими единицами изме-
рения: 601° =1′ (угловая минута), 601′ =1′′ (угловая секунда). Градусной мерой угла пользуются в оптических приборах.
Минута — от латинского minuta — уменьшенное (частица), от minuo — уменьшаю, разбиваю на мелкие части.
Секунда — от латинских secunda (division gradi) —
второе (деление градуса), secundus — следующий.
В технике за единицу измерения углов принимают полный
оборот, в военном деле — «тысячную», то есть |
1 |
часть развер- |
|
3000 |
|||
|
|
нутого угла, или большое деление угломера, равное 100 «тысяч-
ным». В мореходстве единицей измерения является румб, равный
1 части полного оборота.
32
Тригонометрические функции числового аргумента |
241 |
Контрольные вопросы
1°. |
Можно ли осуществить поворот часовой стрелки на: |
||||
|
а) 270°; б) 360°; в) 450°; г) –60°; д) –290°; е) –512°? |
||||
2°. |
Чему равны в радианах величины углов: |
||||
|
а) правильного треугольника; |
||||
|
б) прямоугольного равнобедренного тре- |
||||
|
угольника? |
|
|
|
|
3°. |
Чему равна радианная мера угла АОВ, |
||||
|
изображенного на рис. 273, если длина |
||||
|
дуги MN равняется 0,5 ON? |
||||
4. |
Чему равняется в градусной мере угол |
||||
|
поворота маховика, сделавшего по часо- |
|
|
||
|
|
||||
|
вой стрелке: |
2) 1,5 оборота? |
|
|
|
|
1) 1 оборот; |
|
|
||
5. |
Какие углы описывают минутная и ча- |
|
|
||
|
совая стрелки за: |
|
|
|
|
|
1) 20 мин; |
2) 5 часов? |
|
|
|
6. |
Чему равны приближенно градусные и |
|
|
||
|
радианные меры углов вращения, обоз- |
|
|
||
|
|
||||
|
наченных стрелками на рис. 274? |
||||
2. Тригонометрическая окружность
Как известно, между действительными числами 
 и точками координатной прямой существует вза-
и точками координатной прямой существует вза-  имно однозначное соответствие. Представим себе, что точка движется по координатной прямой от начала координат. Если она движется в положительном направлении и пройдет расстояние, равное
имно однозначное соответствие. Представим себе, что точка движется по координатной прямой от начала координат. Если она движется в положительном направлении и пройдет расстояние, равное  трем единицам измерения длины, то она попадет в точку А(3) (рис. 275). Если же она
трем единицам измерения длины, то она попадет в точку А(3) (рис. 275). Если же она
движется в направлении, противоположном направлению координатной прямой, и пройдет то же расстояние, то она попадет в точку В(–3) (рис. 275). Обратите внимание на то, что в обоих случаях расстояние, пройденное точкой, равно модулю координаты точки, в которую она попадает.
Вообще, пусть дано произвольное число t. Будем считать, что точка движется вдоль прямой, причем в положительном направлении, если t > 0, и в отрицательном направлении, если t < 0. Когда пройденное расстояние будет равняться |t|, точка попадет
242 |
Тригонометрические функции |
в положение, соответствующее числу t. Таким образом, каждому действительному числу соответствует одна и только одна точка Рt координатной прямой (рис. 276, а, б). Поэтому мы можем не различать число t и точку Рt.
Точно также мы можем не различать меру угла вращения t и число t. Это дает возможность установить соответствие между действительными числами и точками единичной окружности, пользуясь измерением расстояния вдоль окружности. Для этого на координатной плоскости рассмотрим единичную окружность (то есть окружность радиуса 1) с центром в начале координат
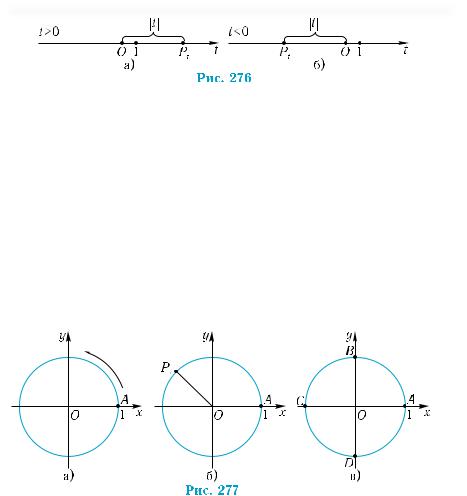
(рис. 277, а) — её называют тригонометрической окружнос-
тью. Точку А с координатами (1; 0) называют началом отсчета (на окружности!). Произвольное число t можно изобразить точкой на тригонометрической окружности.
Пусть задано число t. Представим себе, что некоторая точка движется по тригонометрической окружности. Свое движение она начинает из положения А. Будем считать, что она движется против часовой стрелки, то есть в положительном направлении, если t > 0, и по часовой стрелке, то есть в отрицательном направлении, если t < 0. Если t = 0, то точка находится в положении А. Когда пройденное расстояние будет равняться |t|, точка попадет в положение, соответствующее числу t. Обозначим точку, в которую она попадает, через Рt (рис. 277, б). Понятно, что точка Р0 совпадает с точкой А.

Тригонометрические функции числового аргумента |
243 |
Таким образом, каждому действительному числу t на тригоно- |
|
метрической окружности соответствует точка Рt. По построению, точку Рt получают из точки А поворотом ее вокруг начала координат на t радиан, поскольку на единичной окружности длина
пройденного пути равна модулю радианной меры угла поворота. |
||||||||
|
Пользуясь приведенным построением, нетрудно указать точки |
|||||||
тригонометрической |
окружности, |
соответствующие |
числам |
|||||
π |
, − π , π, − π, 3π , |
− 3π ,2π, − 2π, π + 2π и т. п. Действительно, путь |
||||||
2 |
2 |
2 |
2 |
2 |
1 длины окружности, ведь |
|||
длиной π |
вдоль окружности равен |
|||||||
|
2 |
|
|
|
4 |
|
|
|
длина единичной окружности равна 2π. Точка Pπ совпадает с точ- |
||||||||
|
|
|
|
|
|
2 |
|
|
кой В (рис. 277, в). В точку Рπ можно попасть, если пройти в поло- |
||||||||
жительном направлении расстояние |
π, то есть длину единичной |
|||||||
полуокружности. Точка Р совпадает с точкой С. В точку P |
|
мож- |
||||||
|
|
|
|
π |
|
−π |
|
|
|
|
|
|
|
|
|
2 |
|
но попасть, преодолев в отрицательном направлении четвертую |
||||||||
часть единичной окружности. Точка |
P |
π совпадает с точкой D. |
||||||
|
|
|
|
|
− |
2 |
|
|
Аналогично, точки P3π , P−π будут совпадать соответственно c точ-
2
ками D, С.
!Продолжая эти построения, придем к выводу, что раз-
личным числам может соответствовать одна и та же точка тригонометрической окружности.
Эта неоднозначность напоминает такую реальную ситуацию:
велотрек имеет длину 350 м, велосипедист находится на рас-
стоянии 150 м от финиша. Какой путь он проехал?
Если он только начал соревнование, то он проехал 350 – 150 = = 200 м, если уже проехал один круг, то — (200 + 350 1) м = 550 м, два круга — (200 + 350 2) м = 900 м; если проехал п кругов, то путь будет равняться (200 + 350 п) м. Потому однозначного ответа на поставленный вопрос дать невозможно.
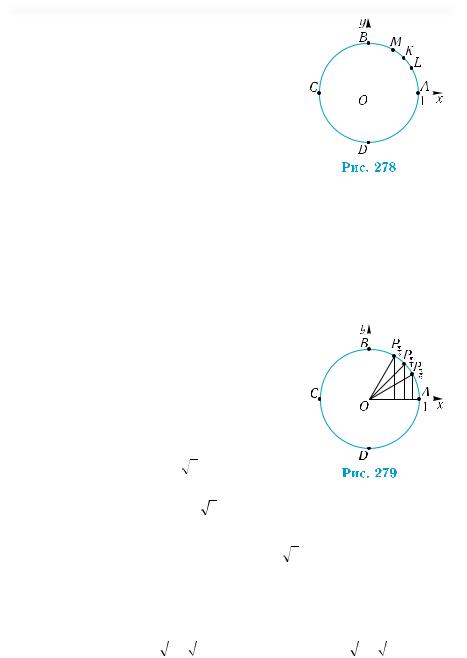
Пример 3. Изобразить на тригонометрической окружности точки, соответствующие числам 6π; 4π; 3π.
244 |
|
|
Тригонометрические функции |
|||||
Разделим дугу АВ, длина которой рав- |
|
|
||||||
|
||||||||
на |
π |
, пополам точкой K, на три равные час- |
|
|
||||
|
2 |
|
|
|
|
|
|
|
ти — точками L и М (рис. 278). Тогда длины |
|
|
||||||
дуг |
|
АL, АK, АM |
соответственно равны |
|
|
|
|
|
|
|
|
|
|||||
π; |
π |
; π. Следовательно, числу π соответству- |
|
|
||||
6 |
4 |
3 |
|
6 |
|
|
|
|
етточкаL,числу π |
—точкаK, числу π — точ- |
|
|
|||||
|
||||||||
|
|
4 |
|
3 |
|
|
|
|
ка М. Эти точки можно соответственно обоз- |
||||||||
начить через Pπ , |
Pπ , Pπ . |
|||||||
|
|
6 |
4 |
3 |
|
|
|
|
Для точек, построенных в примере 3, нетрудно указать прямо-
угольные координаты, пользуясь соотношениями между сторонами и углами прямоугольных треугольников.
Пример 4. Найти прямоугольные координаты точек Pπ , Pπ , Pπ .
Для точки Pπ решение сводится к на- |
|
|
|
|
|
6 |
4 |
3 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
хождению катетов6прямоугольного треуголь- |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
ника, гипотенуза которого равна 1, а один из |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
острых углов составляет |
|
π |
= 30° (рис. 279). |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
Катет, лежащий против угла 30° равен |
, а |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
прилежащий катет равен |
|
|
|
|
|
. Следователь- |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
но, координаты точки P |
— |
|
|
|
; |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Аналогично находятся координаты |
|
1 |
; |
3 |
|
точки P |
|
. Нахожде- |
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
2 |
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|||||
ние координат точки Pπ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||||
|
|
сводится к нахождению катетов прямо- |
|||||||||||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
угольного равнобедренного треугольника, гипотенуза которого рав- |
|||||||||||||||||||||||||||||
на 1. Его катеты равны |
|
2 |
|
; |
2 |
|
. Следовательно, P |
|
2 |
; |
2 |
|
. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2 |
|
|
2 |
|
|
2 |
2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||||||
Тригонометрические функции числового аргумента |
245 |
|
3 |
|
1 |
|
|
2 |
|
2 |
|
|
1 |
|
3 |
|
||
Ответ. |
|
|
|
; |
|
|
; |
|
; |
|
|
; |
|
; |
|
. |
2 |
|
2 |
2 |
2 |
2 |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Пользуясь результатом решения примера 3, можно |
|||||||||||||
|
|
|
||||||||||||||
|
|
|
находить на тригонометрической окружности точ- |
|||||||||||||
|
|
|
ки, соответствующие числам, выраженным в долях |
|||||||||||||
|
|
|
числа π. |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 5. Изобразить на тригонометрической окружности точ-
ки, соответствующие числам |
3π |
; − |
|
5π |
; |
4π |
; |
25π |
. |
|
|
|
|
|
||||
|
6 |
3 |
|
|
|
|
|
|
|
|||||||||
|
4 |
|
|
|
6 |
|
|
|
|
|
|
|
||||||
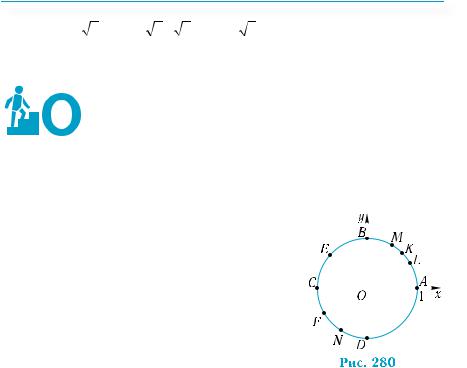
Построение будем выполнять, пользу- |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
ясь рис. 278. Отложим трижды от точки А |
|
|
|
|
|
|
|
|
|
|||||||||
дугу АK (точки K, L, М определены в приме- |
|
|
|
|
|
|
|
|
|
|||||||||
ре 3) в положительном направлении (ее дли- |
|
|
|
|
|
|
|
|
|
|||||||||
на равна π ). Получим точку Е — середину |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дуги ВС (рис. 280). Она и будет соответство- |
|
|
|
|
|
|
|
|
|
|||||||||
вать числу 3 π |
= 3π . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 |
4 |
|
|
π )отточкиАвотрицательном |
||||||||||||||
ОтложивдугуАL(еедлинаравна |
||||||||||||||||||
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
направлении 5 раз, получим точку F, которая отделяет третью часть |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
− |
π |
|
5π |
. |
|
||||
дуги СD. Эта точка и соответствует числу 5 |
6 |
= − |
6 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Далее, отложив дугу АМ (ее длина равна |
π ) от точки А в поло- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||
жительном направлении 4 раза, получим точку N, отделяющую |
||||||||||||||||||
две трети дуги СD. Эта точка и соответствует числу |
|
4π |
. Наконец, |
|||||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
принимая во внимание, что |
25π |
= |
24π + π |
= 4π + |
π |
, придем к вы- |
|
6 |
|
6 |
|
6 |
|
воду, что числу 25π соответствует точка L. Если бы мы отложили
6
от точки А в положительном направлении 25 раз дугу АL, то получили бы тот же результат.

246 |
Тригонометрические функции |
Координаты точек, построенных в примере 4, позволяют находить координаты точек тригонометрической окружности, соответствующих числам, выраженным в долях числа π.
Пример 6. Найти прямоугольные координаты точек P5π , P7π , P4π .
Построим данные точки (рис. 281). Их |
6 |
4 |
3 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
координаты по модулю совпадают с коорди- |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
натами точек Pπ , Pπ , Pπ , |
найденные в при- |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
6 |
|
|
4 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мере 4. Следует лишь определить их знаки. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Точка P5π |
|
находится во второй координат- |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ной четверти, поэтому ее абсцисса отрица- |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
тельна, а ордината положительна. Следова- |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
тельно, |
|
|
|
3 |
; 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
P |
|
− |
.Аналогично получаем: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
5π |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
P 2 |
6 |
|
|
|
|
1 ; − |
3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
; − 2 |
, P |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7π |
|
|
|
|
|
|
|
|
4π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4 2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
3 |
|
1 |
|
|
2 |
|
|
2 |
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||
Ответ. |
− |
|
|
; |
|
|
|
; |
|
|
; − |
|
|
|
; − |
|
; − |
|
. |
|
|
|
|
|
|
|
|
|
||||
|
2 |
2 |
2 |
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Приближенно можно изображать точки тригонометрической окружности, соответствующие произвольным числам.
Пример 7. Изобразить на тригонометрической окружности точки, соответствующие числам 1, –2, 3, –5.
Числу 1 соответствует точка Р1, расположенная на дуге АВ ближе к точке В, так
как длина дуги АВ равна π или прибли- 

жённо 1,5. Чтобы уточнить2ее положение,  отложим от точки А в положительном направлении угол в 1 радиан, приближенно
отложим от точки А в положительном направлении угол в 1 радиан, приближенно 
равный 180π ° ≈ 57,3° (рис. 282). Его можно
построить с помощью транспортира.
Для построения точки Р–2, соответствующей числу –2, отложим от точки А в отрицательном направлении дугу в 2 рад. Соответс-

Тригонометрические функции числового аргумента |
247 |
твующий угол приближенно равен 180π ° 2 ≈115° (см. рис. 282).
Эта точка находится на дуге СD ближе к точке D.
Аналогично строится точка Р3, соответствующая числу 3. Она находится на дуге ВС ближе к точке С (напомним, что точка С
соответствует числу π ≈ 3,14). Числу –5 соответствует та же точка, что и числу −5 + 2π ≈1,28 . Чтобы ее построить, отложим от точки
А в положительном направлении дугу в 1,28 рад. Соответствую-
щий угол приближенно равен 180π ° 1,28 ≈ 73° (см. рис. 282). Точ-
ка Р–5 находится на дуге АВ ближе к точке В (напомним, что точка В соответствует числу π/2 ≈ 1,57.
Соответствие между действительными числами и точками три-
гонометрической окружности, как отмечалось выше, не является |
|||||||||
взаимно |
однозначным. |
Например, |
если рассмотреть |
числа |
|||||
t |
= π |
,t |
= π |
+ 2π , t |
= π + 4π , ..., t |
= π |
+ 2πn,..., то положение точ- |
||
0 |
2 |
1 |
2 |
2 |
2 |
n |
2 |
|
|
ки Pt |
для п = 0, 1, 2, ..., одно и то же — точка Pπ , то есть точка Pπ |
||||||||
|
n |
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
||
соответствует бесконечному множеству чисел 2π, 2π + 2π, 2π + 4π,… . То же самое положение имеют и точки, соответствующие числам
2π −2π, 2π −4π, … . Таким образом, точка Pπ соответствует числам
2
2π + 2πn , где n Z.
!По прямоугольным координатам точки на тригонометрической окружности можно иногда записать соответствующее ей число.
Пример 8. Найти на тригонометрической окружности точки и записать, каким числам они соответствуют, если они имеют:
1) ординату |
2 |
; 2) абсциссу −1 . |
|
|
|||
2 |
|
|
|||||
|
|
2 |
|
|
|||
1) Прямая у = |
2 |
пересекает тригонометрическую окруж- |
|||||
2 |
|||||||
|
|
|
|
π |
|
||
ность в точках Р и Q (рис. 283). Точка Р соответствует числу |
(см. |
||||||
|
|
|
|
|
4 |
|
|
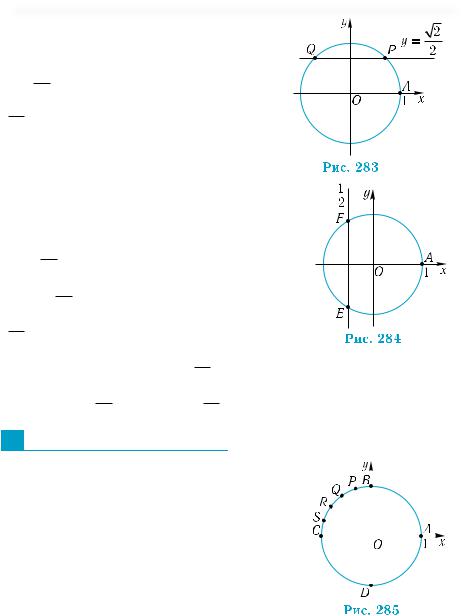
248 Тригонометрические функции
пример 4), а следовательно всем числам 4π + 2πn,n Z . Точка Q соответствует чис-
лу 34π и, следовательно, всем числам
34π + 2πn,n Z .
2) Прямая х = −12 пересекает тригонометрическую окружность в точках Е и F
(рис. 284). Точка Е соответствует числу 4π 


3
(см. пример 6) и, следовательно, всем числам 43π + 2πn,n Z . Точка F соответствует
числу 23π и, следовательно, всем числам
23π + 2πn,n Z .
Ответ. 1) 4π + 2πn,n Z , 34π + 2πn,n Z ;
2)43π + 2πn,n Z , 23π + 2πn,n Z .
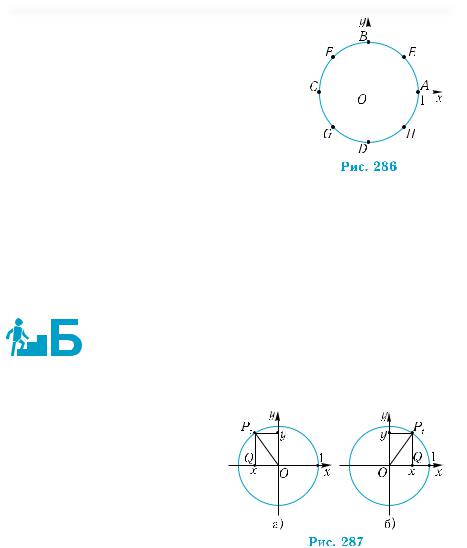
Контрольные вопросы
1°. |
Каким числам соответствуют на рис. 285: |
|
|
||||||||||
|
|
||||||||||||
|
а) середины дуг CD и DА; |
|
|
|
|
||||||||
|
б) точки Р, Q, R, S, делящие дугу ВС на |
|
|
||||||||||
|
пять равных частей? |
|
|
|
|
||||||||
2°. |
На какой из дуг АВ, ВС, CD, DА триго- |
|
|
|
|||||||||
|
|
|
|||||||||||
|
нометрическойокружности(см.рис.285) |
|
|
||||||||||
|
находится точка, соответствующая чис- |
|
|
||||||||||
|
лу 7π; |
9π |
; |
2π |
? |
|
|
|
|
|
|
||
|
|
|
3 |
|
|
|
|
|
|
||||
3°. |
6 |
4 |
|
|
|
|
|
|
|
|
|||
Чему равна длина дуги АD на рис. 285? |
|
|
|||||||||||
4. |
В какой четверти находится точка Рt, если: |
|
|
||||||||||
|
а) t = |
5π |
; |
|
б) t = − |
5π |
; |
в)t = 5,3π ; |
г) t = −2,9π? |
||||
|
4 |
|
|
||||||||||
|
|
|
|
6 |
|
|
|
|
|
||||
Тригонометрические функции числового аргумента |
|
249 |
|||||||||||
5°. |
Каким числам соответствуют на триго- |
|
|
|
|
||||||||
|
|
|
|
||||||||||
|
нометрической окружности (рис. 286) |
|
|
|
|
||||||||
|
точки: |
|
|
|
|
|
|
|
|
|
|
||
|
а) Е, |
F, G, Н, делящие соответственно |
|
|
|
|
|||||||
|
дуги |
АВ, ВС, СD, DА пополам; |
|
|
|
|
|
|
|
||||
|
б) делящие дуги АВ, ВС, СD, DА на три |
|
|
|
|
||||||||
|
равные части? |
|
|
|
|
|
π ], |
|
|
|
|
||
6. |
Найдите числа из промежутка [0; 2 |
|
|
|
|
||||||||
|
которым на единичной окружности со- |
|
|
|
|
||||||||
|
|
|
|
|
|||||||||
|
ответствует точка с: |
|
|
|
в) ординатой –1; |
||||||||
|
а) ординатой 1; |
|
б) ординатой 0; |
|
|||||||||
|
г) абсциссой 0; |
|
д) абсциссой 1; |
|
е) абсциссой –1. |
||||||||
7. |
Какие координаты имеют точки тригонометрической окруж- |
||||||||||||
|
ности, соответствующие числам: |
|
|
|
|
|
|
||||||
|
а) 3π ; |
б) |
19π |
; |
в) − |
π |
; |
|
|
г) 2π ? |
|||
|
|
2 |
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
3. Определение тригонометрических функций |
||||||||||||
|
|
|
Обобщим понятие синуса, косинуса, тангенса и ко- |
||||||||||
|
|
|
|||||||||||
|
|
|
тангенса угла на углы вращения или на произволь- |
||||||||||
|
|
|
ные числа, которые мы договорились не различать. |
||||||||||
|
Пусть задано произвольное число t, определяющее точку Рt на |
||||||||||||
тригонометрической окружности. Обозначим через (х; у) коорди- |
|||||||||||||
наты точки Рt (рис. 287, а). |
|
|
|
|
|
|
|
||||||
Синусом числа t называется ордината точки Pt.
sin t = у.
Косинусом числа t называется абсцисса точки Pt.
cos t = х.
Тангенсом числа t называется отношение синуса числа t к его косинусу.
tg t = cossintt .
Котангенсом числа t называется отношение косинуса числа t к его синусу.
ctg t = cossintt .
250 |
Тригонометрические функции |
Косинус — от латинского complementi sinus: complementus — дополнение, а sinus — впадина, углубление; буквально: дополнение углубления.
Тангенс — от латинского tangens — тот, который касается, tango — касаюсь.
Котангенс — от латинского complementi tangens.
Каждому числу t соответствует единственная точка Pt тригонометрической окружности, а следовательно, единственные абсцисса и ордината этой точки. Собственно, именно поэтому sin t, cos t, tg t, ctg t являются функциями переменной t, принимающей значения из множества действительных чисел. Их называют триго-
нометрическими функциями.
!Дляуглов,рассматриваемыхвгеометрии,приведенные определения совпадают с определениями соответствующих величин в геометрии. Если угол t лежит в первой координатной четверти, то абсцисса и ордината точки Pt являются длинами катетов прямоугольного треугольника ОPtQ (рис. 287, б). В этом случае определения тригонометрических функций совпадают с определениями для острых углов прямоугольного треугольника. В других четвертях значения тригонометрических функций также могут быть найдены из прямоугольных треугольников, только при этом следует учитывать знаки координат точки Pt и связь угла t с острым углом треугольника.
рической окружности, соответствующих ука- |
|
||||
занным числам, то есть точек A = P0 = P2π , |
|
|
|
||
B = Pπ ,C = Pπ , D = P3π (рис. 288). Учитывая, |
функций чи- |
||||
2 |
|
2 |
|
||
что радиус тригонометрической окруж- |
|||||
ности равен 1, будем иметь: Р0(1; 0), |
|||||
Пример |
9. |
Найти значения тригонометрических |
|||
сел 0; π |
; π; |
3π; 2π. |
|
||
2 |
|
2 |
|
|
|
Для решения задачи нужно найти пря- |
|
||||
моугольные координаты точек тригономет- |
|
||||

Тригонометрические функции числового аргумента |
251 |
Pπ (0;1), Pπ ( |
−1; 0), P3π (0; −1). |
Итак, sin 0 = sin 2π = 0, |
sin π |
=1, |
|||||||||||
2 |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
||
3π |
|
|
|
|
|
|
|
|
|
|
3π |
|
|
||
sinπ=0, sin |
= −1, cos0=cos2π=1, cosπ = 0, cosπ=–1, cos |
|
= 0, |
||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
sin 0 |
0 |
|
|
|
|
|
|
|
π |
3π |
не существуют. |
|
|
|
|
tg0 = cos0 = |
1 = 0 = tgπ = tg2π. tg |
2 , tg |
2 |
|
|
|
|
|
|||||||
|
|
|
ctg π |
|
cos |
π |
0 |
|
|
3π; ctg 0, ctg π, ctg 2π не |
|||||
Аналогично |
= |
2 |
= |
= 0 = ctg |
|||||||||||
|
|
1 |
|||||||||||||
|
|
|
2 |
|
sin |
π |
|
|
2 |
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
существуют, так как на нуль делить нельзя. |
|
|
|
|
|||||||||||
Пример 10. Найти значения тригонометрических функций числа 23π .
Нужно сначала найти прямоугольные координаты точки P2π . По модулю они сов-
3 |
|
|
|
|
|
|
|
падают с соответствующими координатами |
|||||||
точки Pπ (рис. 289). Применяя соотношения |
|||||||
3 |
|
|
|
|
|
|
|
между сторонами и углами прямоугольного |
|||||||
треугольника, получим, что P |
1 |
; |
3 |
|
, |
||
|
|
|
|
||||
2 |
2 |
||||||
π |
|
|
|||||
3 |
|
|
|
|
|||
P |
|
− |
1 |
; |
3 |
|
(см. пример 4, п. 2). Поэтому, |
|
|
|
|
|
|||||
|
|
|
||||||
|
2π |
|
2 |
|
2 |
|
||
|
|
|
|
|
|
|
||
3 |
|
|
|
|||||
учитывая определения тригонометрических функций произ-
вольного |
числа, |
будем |
|
|
иметь: |
sin |
|
2π |
= |
|
3 |
; |
cos |
2π |
= − |
1 |
; |
|||||||||||
3 |
|
2 |
|
2 |
||||||||||||||||||||||||
|
|
|
|
|
2π |
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
3 |
|
|
||||||
|
2π |
|
sin |
|
|
ctg 2π |
|
|
cos |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||
tg |
= |
3 |
= − |
3; |
= |
3 |
= = − |
. |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
2π |
|
|
|
|
|
|
|
||||||||||||||||||
3 |
|
|
2π |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
cos |
|
|
3 |
|
|
sin |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Ответ: |
|
3 |
; − 1 |
; − |
3; − |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
252 Тригонометрические функции
Знаки значений тригонометрических функций числа t определяются положением точки Pt на тригонометрической окружности.
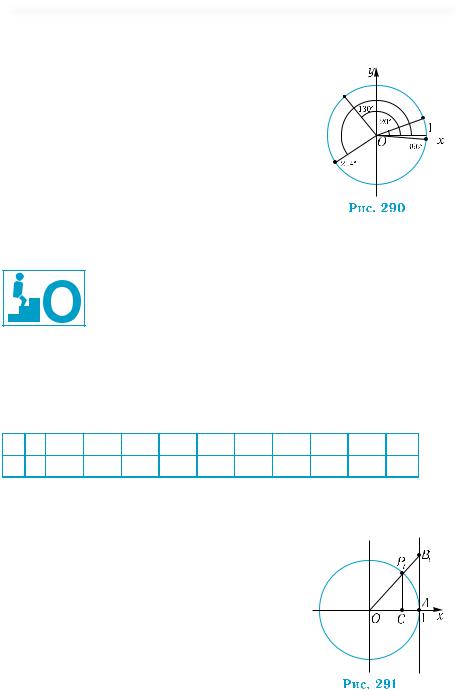
Пример 11. Определить знаки чисел: sin 20°; cos 130°; tg 214°; ctg 356°.
Построим на тригонометрической ок-
ружности точки, соответствующие углам вра-
щения на 20°; 130°; 214°; 356° (рис. 290). 
Далее, воспользовавшись определениями три- |
||||||
гонометрических |
функций, будем |
иметь: |
||||
sin 20° > 0, cos 130° < 0, tg214° = |
sin |
214° |
> 0, |
|||
cos |
214° |
|||||
|
cos356° |
|
|
|||
ctg356° = |
< 0 . |
|
|
|||
sin356° |
|
|
||||
|
|
|
|
|
||
При вычислении значений тригонометрических фун- 
 кций числа (или, что то же самое, меры угла враще-
кций числа (или, что то же самое, меры угла враще-  ния, заданной в радианной мере) с помощью калькулятора переключатель устанавливают в положение Р (радиан). То же самое делают при нахождении значения аргумента
ния, заданной в радианной мере) с помощью калькулятора переключатель устанавливают в положение Р (радиан). То же самое делают при нахождении значения аргумента
по заданному значению тригонометрической функции.
Пример 12. Составить таблицу значений функции h = t + sin t
для таких значений t: 0; 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,8; 0,9; 1.
Чтобы выполнить задание, воспользуемся калькулятором.
t |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
h |
0 |
0,200 |
0,399 |
0,596 |
0,789 |
0,979 |
1,16 |
1,34 |
1,52 |
1,68 |
1,84 |
|
|
Синус и косинус произвольного числа мы определили геометри- |
|||||||||||
чески. В то же время тангенс и котангенс ввели как некоторые отношениясинусаикосинуса.Однакоихтакжеможноохарактеризовать геометрически. 
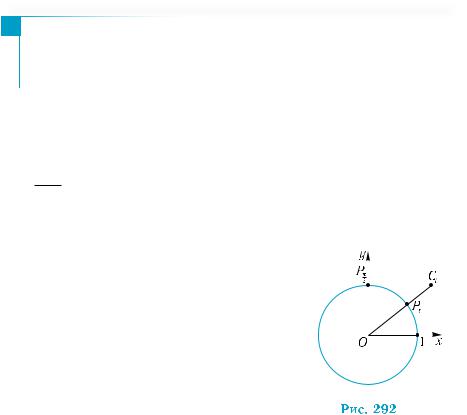
Прямая, проходящая через точку с координатами (1; 0) перпендикулярно оси абсцисс, называется линией
тангенсов (рис. 291).
Линия тангенсов имеет уравнение х = 1, ее можно считать координатной прямой с направлением и масштабом оси у и с началом в точке А.
Тригонометрические функции числового аргумента |
253 |
! Каждому числу t ≠ 2π(2n +1), n Z, можно поставить в
соответствие точку Вt на линии тангенсов, являющуюся точкой пересечения прямой OPt с линией тангенсов.
Докажем, что ордината точки Вt равна tg t, если точка Рt находится в первой четверти.
Из подобия треугольников OPt С и ОВtА имеем: OCPCt = ABOAt ,
или sincostt = AB1 t , tgt = ABt .
Этот вывод остаётся правильным и тогда, когда точка Pt |
на- |
||||||
ходится не в первой четверти тригонометрической окружности. |
|||||||
Предлагаем убедиться в этом самостоятельно. |
|
|
|
|
|
|
|
Прямая, проходящая через точку с |
|
|
|
|
|
|
|
координатами (0; 1) перпендикуляр- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
но оси ординат, называется линией |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
котангенсов (рис. 292). |
|
|
|
|
|
|
|
Линия котангенсов имеет уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у = 1, ее также можно считать координатной |
|
|
|
|
|
|
|
прямой с направлением и масштабом оси х |
|
|
|
|
|
|
|
и с началом в точке Pπ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
пересечения |
|||||
Докажите самостоятельно, что абсцисса точки Ct |
|||||||
прямой OPt с линией котангенсов равна ctg t. |
|
|
|
|
|
|
|
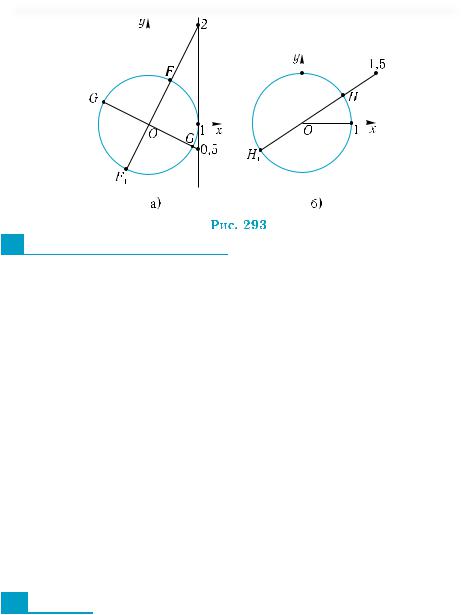
Пример 13. Изобразить на тригонометрической окружности точки Pt если: 1) tgt = 2; 2) tgt = – 0,5; 3) ctgt = 1,5.
1) Отложим на линии тангенсов в положительном направлении отрезок, равный 2 (напомним, что радиус окружности равен 1). Через полученную точку и центр тригонометрической окружности проведем прямую. Точки F и F1 пересечения этой прямой с окружностью и будут искомыми (рис. 293, а).
2) В отрицательном направлении линии тангенсов отложим отрезок длиной 0,5. Далее задача решается аналогично предыдущей. Точки G и G1 являются искомыми (см. рис. 293, а).
3) Отрезок длиной 1,5 откладываем в положительном направлении линии котангенсов. Далее задача решается аналогично предыдущей. Точки Н и Н1 являются искомыми (рис. 293, б).
254 |
|
|
|
Тригонометрические функции |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы |
|
|
|
|
|
1°. |
Дана точка Рt(–0,8; 0,6) на тригонометрической окружности. |
|||||
|
Чему равен: а) sin t; б) cos t; в) tg t; г) ctg t? |
|
|
|
|
|
2°. |
Может ли синус некоторого числа равняться 7; |
8 |
; − 7; − |
8 |
; π; |
|
|
π? |
8 |
7 |
8 |
7 |
3 |
|
|
|
|
|
|
|
3. |
4 |
|
|
|
|
|
Сколько чисел t, удовлетворяющих условию cos t = 1, содер- |
||||||
|
жится в промежутке [0; 4π]? |
|
|
|
|
|
4. |
Всегда ли существует на промежутке [0; π] число, удовлетво- |
|||||
|
ряющее условию tg t = а, где а — произвольное действитель- |
|||||
|
ное число? |
|
|
= 0,4, содер- |
||
5. |
Сколько чисел t, удовлетворяющих условию sin t |
|||||
|
жится в промежутке [0; 2π]? |
|
|
|
|
|
6. |
Верно ли, что числам π |
и 5π соответствует одна и та же точ- |
||||
|
ка на линии тангенсов4? |
4 |
|
|
|
|
7. |
Существуют ли на промежутке [0; π] числа t, для которых |
|||||
|
sin t = –0,1? |
|
|
|
|
|
Задачи
228°. Запишите в радианной мере значения углов: |
|||||
1) |
120°; |
2) 54°; |
3) |
210°; |
4) 165°; |
5) |
–330°; |
6) 27°; |
7) |
127°12'. |
|

Тригонометрические функции числового аргумента |
255 |
229°. Запишите в градусной мере значения углов:
1)3 ; 2) −56π ; 3) 2; 4) 3π; 5) 54π; 6) −53π; 7) 32π.
230.Изобразите на тригонометрической окружности углы вращения, радианные меры которых равны:π
1°) |
3π |
; |
2°) − |
π |
; 3) 2; |
4) –3; |
5) 0,5; |
6) –6. |
|
2 |
2 |
||||||||
|
|
|
|
|
|
|
231. Зубчатое колесо имеет 40 зубцов. Выразите в градусах угол, на который повернётся колесо при повороте на 1 зубец; 15
зубцов; 80 зубцов; 150 зубцов.
232. Среди мер углов вращения –310°, –220°, –50°, 770° укажите такие, в которых положение подвижного луча совпадает с положением подвижного луча угла, градусная мера которо-
го равна: 1) 50°; 2) 140°.
233. Среди мер углов вращения −187π , −107π , −137π , − 37π , 67π ука-
жите такие, в которых положение подвижного луча совпадает с положением подвижного луча угла, радианная мера
которого равна: 1) 7π ; 2) 47π .
234. Найдите длину дуги, если известны ее радианная мера α и радиус R окружности, содержащей ее:
1) α = 3, R = 1 см; 2) α = 23π , R = 3 см; 3) α = 45π , R = 5 м.
235. Колесо при равномерном движении за 10 с повернулось на 5π рад. С какой угловой скоростью оно вращается?
236. Шкив скоростного электродвигателя делает 90 000 оборотов за минуту. Найдите угловую скорость вращения этого шкива: 1) в град/с; 2) в рад/с.
237. Клеть шахтного подъемника поднимается на 100 м за 40 полных оборотов вала подъемника в положительном направлении. Определите в радианах угол поворота вала подъемника, если клеть поднялась на 13,75 м; опустилась на 21 м.
238. Точка движется равномерно по окружности радиуса R = 60 см с угловой скоростью ω = 4π рад/с. Найдите ее линейную скорость.
256 |
Тригонометрические функции |
239.Точка движется равномерно по окружности радиуса R = 30 см с линейной скоростью 75 см/с. Найдите ее угловую скорость.
240.Какую линейную скорость имеет точка вращающегося диска, когда она удалена на 18 см от оси вращения, а угловая скорость вращения диска равна 3π рад/с? Какой длины дугу опишет эта точка за 45 с?
241.Изобразите на тригонометрической окружности точки, соответствующие числам:
1°) − |
π |
; − |
π |
; − |
|
π |
, |
2π , |
3π , |
5π |
; |
2) 1,5; 2,3; |
|
|
|
|
3) 5π |
; − 27π . |
|||||||||||||||||||
|
|
6 |
|
|
|
4 |
|
|
|
3 |
|
3 |
|
4 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|||
242. Найдите прямоугольные координаты точек: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
1°) P |
|
, P |
|
, P |
|
; |
|
|
|
|
|
|
|
2°) P |
5π |
, P |
|
|
, P |
2 |
|
; |
|
|
|
|
|
||||||||||
|
|
7π |
|
|
3π |
|
5 |
π |
|
|
|
|
|
|
|
|
− |
|
|
− |
π |
|
− |
π |
|
|
|
|
|
|
|||||||
|
|
6 |
|
|
|
|
4 |
|
3 |
|
; |
|
|
|
|
|
|
4) P |
6 |
|
|
|
4 |
|
|
3 |
|
|
|
|
|
|
|||||
3) P |
, P |
|
, P |
|
|
|
|
|
|
|
, P |
7π |
, P |
. |
|
|
|
|
|
|
|
||||||||||||||||
11π |
|
|
− |
5π |
|
−4π |
|
|
|
|
|
|
|
−π |
|
|
− |
|
|
2 |
π |
|
|
|
|
|
|
|
|
||||||||
|
6 |
|
|
|
|
4 |
|
|
|
|
3 |
|
|
|
|
|
|
|
6 |
|
|
|
4 |
|
|
3 |
|
|
|
|
|
|
|
|
|||
243. Найдите координаты точки тригонометрической окружнос- |
|||||||||||||||||||||||||||||||||||||
ти, полученной при повороте точки (1; 0) на угол: |
|
|
|
|
|
||||||||||||||||||||||||||||||||
1°) 3π; |
|
|
|
|
|
|
|
2°) – 2π; |
|
3°) 4,5π; |
4) |
π |
; |
|
|
|
|
5) 225°. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
244. Найдите углы, на которые нужно повернуть точку (1; 0) вокруг |
|||||||||||||||||||||||||||||||||||||
начала координат, чтобы получить точку с координатами: |
|
|
|||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
|
2 |
|
2 |
|
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
||||||||
1°) |
|
|
|
; |
|
|
|
|
; 2) |
− |
|
|
; |
|
|
;3) − |
|
|
|
; − |
|
|
|
; 4) |
|
; − |
|
|
. |
||||||||
2 |
|
|
2 |
|
|
2 |
2 |
|
2 |
|
|
2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
245.Изобразите на тригонометрической окружности точки и запишите, каким числам они соответствуют, если они имеют:
1) ординату − |
3 |
; |
2) абсциссу |
|
|
2 |
. |
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
5 |
|
4 |
|
|||||
|
|
|
|
|
π |
|
π |
|
|
|
|||||
246. Для каждого из приведенных значений t |
|
|
; |
; |
π; π; |
π; |
|||||||||
t = |
4 |
2 |
6 |
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
3 |
π; |
11 |
π |
|
укажите такое значение t′ , чтобы точки Р и P |
|
2 |
|
6 |
|
|
t |
t′ |
|
|
|
|
|
||
были симметричными относительно: 1) начала координат; 2) оси абсцисс; 3) оси ординат; 4)* прямой у = х; 5*) прямой
у = –х.

Тригонометрические функции числового аргумента |
|
|
|
|
|
|
257 |
|||||||||
247*. Числа заданы формулой: 1) |
t = π k , 2) |
t = π k , |
3) |
t = π k , |
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
4 |
4) t = |
π (2k +1), где k = 0, ±1, ±2, ±3, ... . Изобразите на коорди- |
|||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
натной прямой и на тригонометрической окружности точки, |
||||||||||||||||
соответствующие этим числам. Сколько таких точек будет на |
||||||||||||||||
координатной прямой и сколько — на тригонометрической ок- |
||||||||||||||||
ружности? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
248°. Даны координаты точки Рt |
на тригонометрической окруж- |
|||||||||||||||
ности. Вычислите sin t, cos t, tg t, ctg t. |
|
|
|
|
|
|||||||||||
4 |
|
3 |
|
|
5 |
|
12 |
|
3 |
; 1 |
|
|
3 ; |
7 |
|
|
1) |
; − |
|
; |
2) − |
|
|
; |
; |
3) − |
; |
4) |
. |
||||
5 |
13 |
|
||||||||||||||
|
4 |
|||||||||||||||
5 |
|
|
|
|
13 |
|
2 2 |
|
|
4 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
249°. Вычислите значения тригонометрических функций чисел:
1) |
|
3π |
; |
|
2) |
2π |
; |
3) |
5π |
; |
4) |
7π . |
|||||||
4 |
|
3 |
4 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
||||
250°. Определите знаки тригонометрических функций sin t, cos t, |
|||||||||||||||||||
tg t и ctg t для t, равных: |
|
|
|
|
|
|
|||||||||||||
1) |
7π ; |
2) |
− |
5π |
; 3) |
12π |
; 4) |
−7π ; 5) 7π ; |
6) |
13π |
. |
||||||||
|
7 |
|
|
||||||||||||||||
|
6 |
|
|
3 |
|
|
|
|
|
|
6 |
9 |
6 |
|
|||||
251°. Вычислите: |
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|||||
1) |
sin π + cos π −2tg2π + ctg |
; |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
2) |
sin −3π − cos − π + 2tg3π + ctg −5π . |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
||
252. Изобразите на тригонометрической окружности точки Рt |
|||||||||||||||||||
если: |
|
2) сtg t = 2; |
3) сtg t = –0,5; 4) tgt = 1,5; 5) tgt = –1. |
||||||||||||||||
1) сtg t = 1; |
|||||||||||||||||||
Найдите все числа из промежутка [0; 2π], удовлетворяющие |
|||||||||||||||||||
условию: |
0; |
2) cos t = l; |
3) cos t = –1; 4) ctg t = 0; 5) sin t = –1. |
||||||||||||||||
1) sin t = |
|||||||||||||||||||
Упражнения для повторения
254.Известно, что sin α = а. Найдите cos α, tg α, если α:
1)острый угол прямоугольного треугольника;
2)тупой угол треугольника.
258 |
Тригонометрические функции |
255.Отношениекатетовпрямоугольноготреугольникаравно4:3. Найдите синусы и косинусы острых углов треугольника.
256.Докажите, что точка с координатами (cos α; sin α) лежит на окружности радиуса 1 и с центром в начале координат.
257.Из заданного равенства выразите х через у и у через х:
1)х2 + у2 = 4, если x > 0, y > 0;
2)1 − x12 = y2 , если x < 0, y < 0.
258.Даны углы: 30°; 64°; 10°; α; 45° + α; 8π. Найдите меры углов:
1)дополняющих их до прямых; 2) смежных с ними.
|
|
Итог |
|||
Основные понятия |
|||||
Определение |
Геометрическая |
||||
|
интерпретация |
||||
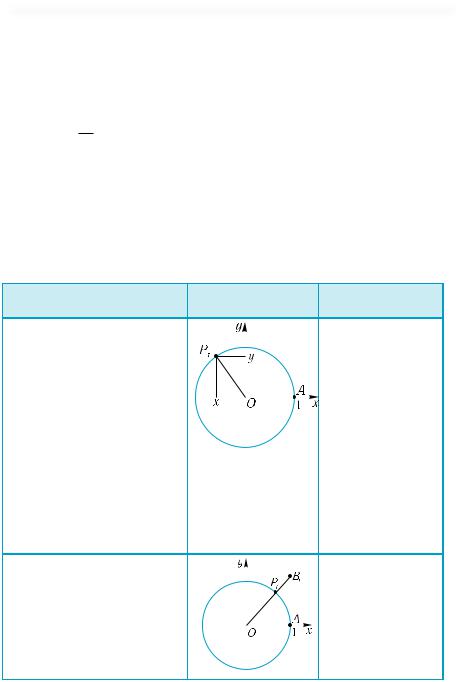
Синус числа t — ордината |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
точки Рt. |
|
|
|
|
|
Косинус числа t — абсцис- |
|
|
|
|
|
са точки Рt. |
|
|
|
|
|
Тангенс числа t — отно- |
|
|
|
|
|
|
|
|
|
|
|
шение синуса числа t к его |
|
|
|
|
|
косинусу. |
|
|
|
|
|
Котангенс числа t — отно- |
|
|
|
|
|
шение косинуса числа t к |
|
|
|
|
|
sin t = у; cos t = х |
|||||
его синусу. |
tgt = sint ; |
||||
|
|||||
|
|
cost |
|||
|
ctgt = cost |
||||
Линия тангенсов — пря- |
|
sint |
|||
|
|
|
|
|
|
|
|
|
|
|
|
мая, проходящая через |
|
|
|
|
|
точку (1; 0) перпендику- |
|
|
|
|
|
лярно оси абсцисс, то есть |
|
|
|
|
|
прямая х = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Применение
Тригонометрические функции применяются для решения треугольников, исследования вращательного движения и т. п.
Геометрическая
интерпретация
тангенса
Тригонометрические функции числового аргумента |
259 |
||||||
Определение |
Геометрическая |
Применение |
|||||
интерпретация |
|||||||
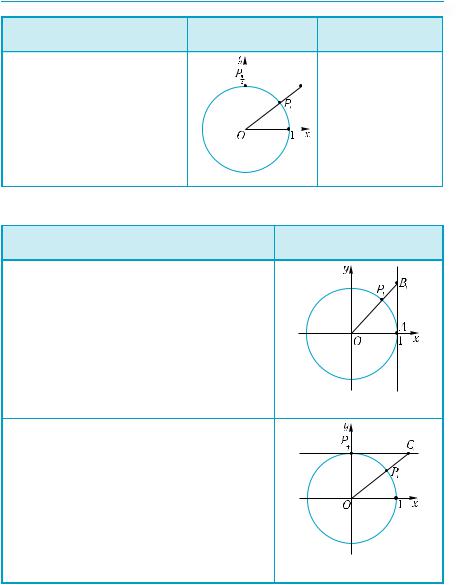
Линиякотангенсов—пря- |
|
|
|
Геометрическая |
|||
|
|||||||
мая, проходящая |
через |
|
|
|
интерпретация |
||
точку (0; 1) перпендику- |
|
|
|
|
|
котангенса |
|
лярно оси ординат, то есть |
|
|
|
|
|||
прямая у = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Основные утверждения
Формулировка Геометрическая интерпретация
Ордината точки Вt пересечения прямой ОPt, соединяющей центр тригонометрической окружности с точкой Рt, с линией тангенсов равна tg t.
tg t = yBt
Абсцисса точки Сt пересечения прямой ОPt, соединяющей центр тригонометрической окружности с точкой Рt, с линией котангенсов равна сtg t.
ctg t = xCt
