
- •Обращение к читателю
- •Введение
- •РАЗДЕЛ 1. Функции, их свойства и графики
- •§1. Числовые множества
- •§2. Вычисления и расчёты
- •§3. Функциональные зависимости
- •§4. Основные свойства функций
- •§5. Корни n-ой степени
- •§6. Степенные функции с рациональными показателями
- •§7. Основные понятия и аксиомы стереометрии
- •§8. Взаимное расположение двух прямых в пространстве
- •§9. Параллельное проектирование
- •§10. Изображение фигур в стереометрии
- •§11. Параллельность прямых и плоскостей
- •§12. Параллельность плоскостей
- •§13. Тригонометрические функции числового аргумента
- •§14. Основные соотношения между тригонометрическими функциями
- •§15. Свойства и графики тригонометрических функций
- •§16. Тригонометрические формулы сложения и следствия из них
- •§17. Простейшие тригонометрические уравнения и неравенства
- •§18. Перпендикулярность прямой и плоскости
- •§19. Связь между параллельностью и перпендикулярностью прямых и плоскостей
- •§20. Перпендикулярность плоскостей
- •§21. Ортогональное проектирование
- •§23. Измерение расстояний в пространстве
- •§24. Измерение углов в пространстве
- •Ответы и указания к задачам
- •Предметный указатель
- •Содержание

§1. Числовые множества
Понятие числа относится к основным в математике. С ее развитием развивалось и обогащалось само понятие числа.
В этом параграфе сделан обзор основных числовых систем, изучавшихся ранее, подробнее рассматриваются множества рациональных и действительных чисел.
1. Множество рациональных чисел
Первоначальные представления о числах формировались постепенно под влиянием практической деятельности человека. С древних времен числа употреблялись: а) при счете; б) при измерении величин.
Изучение математики начинается со знакомства с натуральными числами, то есть с числами 1, 2, 3, 4, 5, …, используемыми при счете. При сложении и умножении натуральных чисел всегда получают натуральные числа. Но разность и частное от деления натуральных чисел могут не быть натуральными числами.
Если присоединить к натуральным числам отрицательные числа и нуль, то множество натуральных чисел расширяется до множества целых чисел. Отрицательные целые числа вместе с натуральными позволяют характеризовать изменение численности какого-либо множества с учётом направления изменения. Например, если количество изделий, изготовленных рабочим за смену, изменились на + 20, то это означает, что оно увеличилась на 20, а если на –20, то — уменьшилось. То же самое относится к записи размера прибыли и убытка, температуры воздуха, скорости движения по течению и против течения реки и т. п.
Для любых целых чисел их сумма, разность и произведение являются целыми числами. Однако частное от деления двух целых чисел может не быть целым числом.

Числовые множества |
19 |
Дробные числа появились как результат измерения. Пусть нужно измерить длину классной доски. Допустим, что в длине классной доски уложился один метр и образовался остаток, меньший метра. В таком случае разделим метр, например, на 10 равных частей, измерим остаток десятыми долями метра и находим, что остаток содержит 7 десятых частей метра. Получили дробное
число 1107 . Целые числа вместе с дробными образуют множество рациональных чисел. При выполнении четырех арифмети-
ческих действий (кроме деления на 0) над рациональными числа-
ми всегда получают рациональные числа. Каждое рациональное
число можно представить в виде обыкновенной дроби mn , где т —
целое число, п — натуральное.
Множество натуральных чисел обычно обозначают буквой N, множество целых чисел — Z, множество рациональных чисел — Q.
Каждое рациональное число можно представить также в виде десятичной дроби, конечной или бесконечной. Например,
18 = 0,125; 2257 = 210028 = 2,28; 19 = 0,1111....
Последняя десятичная дробь является периодической с пери-
одом 1 и её записывают так: 0,(1) (читается: нуль целых и одна десятая в периоде).
Различные бесконечные десятичные дроби изображают различные рациональные числа. Исключение составляют дроби с периодом 9, которые можно считать другой записью дробей с периодом 0: 1,(9) =
= 1,999... = 2,000... = 2; 0,3(9)= 0,3999... = 0,4000... = 0,4. Для беско-
нечных десятичных дробей с периодом 9, как правило, применяют запись дробями с периодом 0. Если отождествить периодические дроби с периодом 9 с соответствующими периодическими дробями с периодом 0, то между рациональными числами и десятичными периодическими дробями будет существовать взаимно однозначное соответствие.
Òеîрема 1. Каждое рациональное число m можно пред- n
ставить в виде десятичной периодической дроби.

20 |
Функции, их свойства и графики |
Утверждение вытекает из того, что в процессе деления числителя m на знаменатель п после выделения целой части каждый из остатков будет меньше п, то есть остаток может равняться одному из чисел 0, 1, 2, …, п – 1. Поэтому не позже, чем после п-го шага, какой-то из остатков повторится, и, следовательно, в частном будет повторяться та же группа цифр.
!Если при делении «уголком» получают конечную десятичную дробь, то её всегда можно записать в виде периодической с периодом, равным нулю, приписав справа в качестве десятичных знаков бесконечное множество нулей.
Пример 1. |
Записать числа |
9 |
и |
3 |
в виде десятичной пери- |
|||||
40 |
25 |
|||||||||
одической дроби. |
|
|
|
|
|
|||||
|
|
|
|
|
3 |
|
||||
Имеем: |
9 |
|
= 0,225 = 0,225000... = 0,225(0), |
= 0,12 = |
||||||
40 |
|
25 |
||||||||
|
|
|
|
|
|
|
|
|||
= 0,12000... = 0,12(0). |
|
|
|
|
|
|
||||
Ответ. 0,225(0); 0,12(0). |
|
|
|
|
|
|
||||
Заметим, что знаменатели дробей, рассмотренных в примере 1, своими простыми множителями имеют лишь числа 2 и 5: 40 = 23 5, 25 = 52. Оказывается, что и вообще, если знаменатель дроби имеет своими простыми множителями лишь числа 2 и 5, то такая дробь обращается в конечную десятичную дробь.
Дроби, знаменатели которых в своих разложениях на простые множители содержат числа, отличные от 2 и 5, обращаются в бесконечные десятичные дроби.
Пример 2. Записать каждое из чисел 53 , 569 , 56 , 112 , 358 в виде бесконечной десятичной периодической дроби.
53 =1,6666... =1,(6); 569 = 0,160714285714285... = 0,160(714285);
56 = 0,8333... = 0,8(3); 112 = 0,18181818... = 0,(18); 358 = 0,2285714285714... = 0,2(285714).

Числовые множества |
21 |
Если х — отрицательное рациональное число, то в виде бесконечной десятичной дроби представляют ему противоположное число и перед полученным числом ставят знак «минус».
Справедливо и утверждение, обратное теореме 1.
Òеîрема 2. Каждая десятичная периодическая дробь
изображает определенное рациональное число.
Если десятичная дробь имеет своим периодом число 0, то это утверждение очевидно. Например, 2,73(0) = 2,73000... = 2,73 = 100273.
В общем случае можно воспользоваться формулой суммы бесконечно убывающей геометрической прогрессии:
S = 1a−1q ,
где а1 — первый член геометрической прогрессии, q — ее знаменатель (|q| < 1).
Пример 3. Записать в виде обыкновенной дроби периодичес-
кую дробь: 1) 3(7); 2) 1,5(38).
1) Запишем периодическую десятичную дробь без скобок: 3,7777... . Представим полученную дробь в виде суммы целой части, десятых, сотых и так далее долей:
3,7777... = 3 + 107 + 1007 + 10007 +... .
Слагаемые суммы 107 + 1007 + 10007 +... являются членами бесконечно убывающей геометрической прогрессии с первым членом
a1 = 107 и знаменателем q = 101 (|q| < 1).
По формуле суммы бесконечно убывающей геометрической
|
|
|
7 |
|
|
7 |
|
|
7 |
|
|
7 |
|
|
7 |
|
||
прогрессии имеем: |
+ |
+ |
+... = |
|
|
10 |
|
= |
. Следователь- |
|||||||||
10 |
100 |
1000 |
|
1 |
9 |
|||||||||||||
|
|
|
|
1 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
||||
|
7 . |
|
|
|
|
|
|
|
|
10 |
|
|
|
|||||
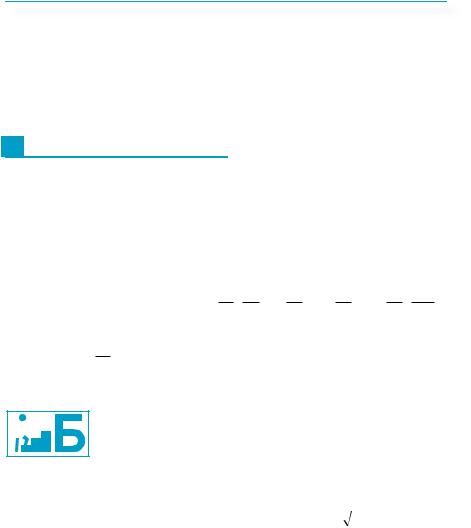
но, 3,(7) = 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
Функции, их свойства и графики |
||||||||||||
|
|
2) 1,5(38) = 1,5383838… = 1 + |
|
5 |
+ |
|
38 |
|
+ |
|
38 |
+... =1 + |
|
5 |
+ |
|||||||||
|
10 |
|
|
|
100000 |
10 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1000 |
|
|
|
|||||||||
+ |
|
0,038 |
=1 + |
|
5 |
|
|
+ |
38 |
=1 + |
5 99 +38 =1 |
433 |
. |
|
|
|
|
|||||||
1 −0,01 |
|
|
|
|
990 |
990 |
|
|
|
|
||||||||||||||
|
10 |
|
|
|
990 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Ответ. 1) 3 |
7 |
; |
|
2)1 |
433. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
9 |
|
|
|
|
990 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 Контрольные вопросы
1°. Верно ли, что:
а) каждое целое число является натуральным; б) каждое целое число является рациональным?
2°. Какое множество дополняет множество целых чисел до множества рациональных чисел?
3°. Чему равен период десятичной дроби 49,35727272...?
4°. Какие из следующих обыкновенных дробей обращаются в ко-
нечные десятичные дроби: 163 , 497 , 56 , 507 ,1511 , 253 , 8021, 212 ,1257 ?
5. Сколько цифр содержит период представления рационально-
го числа 3 в виде бесконечной десятичной дроби?
11
2. Множество действительных чисел
Необходимость расширения множества рациональ- 
 ных чисел обусловлена геометрическими и алгебраическими соображениями. Так, для точного измерения длин отрезков рациональных чисел не хватает.
ных чисел обусловлена геометрическими и алгебраическими соображениями. Так, для точного измерения длин отрезков рациональных чисел не хватает.
Например, не существует рационального числа, равного длине гипотенузы равнобедренного прямоугольного треугольника, если
длина его катета является единицей измерения ( 2 не является рациональным числом!)
Во множестве рациональных чисел не всякое уравнение вида х2 = а имеет решение. Например, уравнение х2 = 2 во множестве рациональных чисел не имеет решений, так как не существует рационального числа, квадрат которого равнялся бы 2.
Новые числа можно ввести, используя бесконечные непериодические десятичные дроби.
В предыдущем пункте было показано, что любое рациональное число можно записать в виде периодической десятичной дроби,

Числовые множества |
23 |
и каждая десятичная периодическая дробь является рациональным числом. Если же бесконечная десятичная дробь не является периодической, то она не является рациональным числом. Например, дробь 0,12345678910111213..., в которой после запятой выписаны все натуральные числа, — непериодическая, а потому она не изображает никакое рациональное число. Данная дробь является иррациональным числом.
Иррациональным числом называется бесконечная десятичная непериодическая дробь.
Примеры иррациональных чисел: 0,35355355535555... (после
первой тройки – одна пятерка, после второй — две и т. д.), 2 =
= 1,41421356..., π = 3,1415926535... (отношение длины окружности к диаметру).
Иррациональные числа х и у, записанные в виде бесконечных десятичных дробей, сравниваются по тем же правилам, что и конечные десятичные дроби. Если целая часть числа х меньше целой части числа у, то х < у. Если целые части двух чисел равны, то для их сравнения придется обратиться к их дробным частям. Например, 12,72241... < 12,72250..., поскольку у этих чисел равны целые части и первые три десятичных знака после запятой, а четвертый знак после запятой у левого числа меньший: 4 < 5.
Рациональные и иррациональные числа образуют множест-
во действительных или вещественных чисел. Это множест-
во обозначают буквой R. Каждое действительное число изображается в виде десятичной дроби (конечной или бесконечной).
Действительныечисламожноскладывать,вычитать,умножать и делить (при условии, что делитель отличен от нуля). Действия над действительными числами обладают теми же свойствами, что и действия над рациональными числами. В прикладных задачах при выполнении действий над действительными числами их заменяют рациональными приближенными значениями.
Пример 4. Две материальные точки вращаются по окружностям радиусов 3 м и 4 м. Каждая из них за 1 с делает один оборот. Какое расстояние они вместе преодолеют за 1 с? Вычисления выполнить с точностью до 1 м.
Искомое расстояние равно сумме длин двух окружностей, описанных данными материальными точками за 1 с. Поскольку длина окружности вычисляется по формуле l = 2πR, где R — ради-

24 |
Функции, их свойства и графики |
ус окружности, l — её длина, то можно вычислить длину каждой окружности (при вычислении сохраняем один дополнительный десятичный знак): l1 = 2π 3 = 6π ≈ 6 3,1 = 18,6 (м), l2 = 2π 4 = 8π ≈ ≈ 8 3,1 = 24,8 (м). Искомое же расстояние равно l1 + l2 ≈18,6 + 24,8 = = 43,4 (м). Округлив результат до 1 м, получим: l1 + l2 ≈ 43 (м).
Ответ. 43 м.
Геометрически действительные числа изображаются точками координатной прямой, то есть прямой с выбранными началом координат, положительным направлением отсчета и единицей масштаба.
Основное свойство действи тельных чисел .
Каждому действительному числу соответствует единственная точка координатной прямой, и наоборот, каждая точка координатной прямой соответствует единственному действительному числу.
Учитывая это соответствие, часто не различают число и изображающую его точку. Например, говорят «точка 5», «точка 2», «точка х» и обозначают соответствующую точку координатной прямой числом «5», «2», «х». Координатную прямую называют также числовой осью. То, что точка А имеет координату х, записывают так: А(х).
Обычно координатную прямую размещают горизонтально, положительное направление выбирают слева направо, начало координат обозначают буквой О. При этом, если а < b, то точка а расположена на числовой оси левее точки b (рис. 2, а); если же а > b, то точка а расположена правее точки b (рис. 2, б).
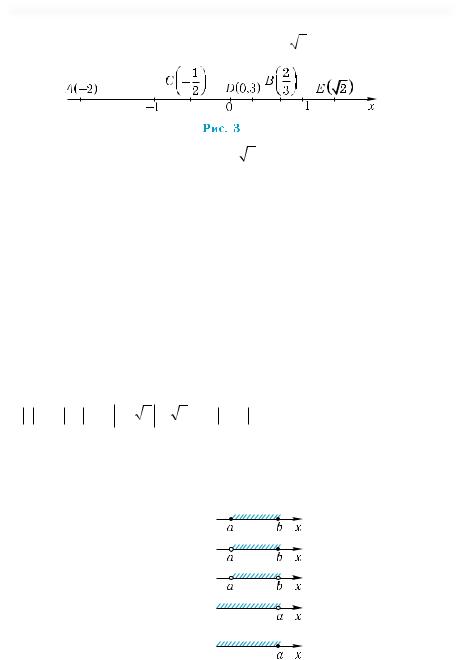
Пример 5. На координатной прямой изобразить точки по их
координатам: |
|
2 |
|
− |
1 |
; D(0,3); E ( 2). |
||
A(−2); B |
3 |
|
; C |
2 |
|
|||
|
|
|
|
|
|
|
||
Точку А(– 2) получим, если на координатной прямой отложим от начала координат в отрицательном направлении две еди-
ницы масштаба (рис. 3). Точку |
|
2 |
можно построить, если раз- |
|
B |
3 |
|
||
|
|
|
|
|
делить единицу масштаба на три равные части и отложить вправо
две такие части. Точки C −1 ; D(0,3) строятся аналогично (еди-
2
Числовые множества |
25 |
ница масштаба делится соответственно на две части и на 10 равных частей). Для изображения точки E ( 2) можно воспользо-
ваться приближенным значениям 2 , например, 1,4.
Геометрическая интерпретация действительных чисел позволяет наглядно ввести понятие модуля числа.
Расстояние от начала координат О до точки х называется модулем числа х и обозначается через |х|.
Из определения вытекает, что при х ≥ 0 расстояние от О до х равняется х, то есть модулем неотрицательного числа является само это число. Если же х < 0, то расстояние от О до х равняется –х, то есть модулем отрицательного числа является противополож-
ное ему число. Следовательно, |
|
x |
|
x, |
eсли x ≥ 0, |
|
|
= |
|
||
|
|
|
|
−x, |
eсли x < 0. |
|
|
|
|
Это равенство можно рассматривать как алгебраическую запись определения модуля действительного числа. Например,
3 = 3, −5 = 5, 1− 2 = 2 −1, x −1 = x −1,eсли x ≥ 1,
1 − x,eсли x < 1.
На координатной прямой также изображают числовые проме-
жутки: отрезки, интервалы, полуинтервалы. Ниже приведена их
запись с помощью скобок, неравенств, а на рис. 4 — изображение |
||
на координатной прямой. |
(отрезок) |
|
[a; b] |
a ≤ x ≤ b |
|
(a; b] |
a < x ≤ b |
(полуинтервал) |
(a; b) |
a < x < b |
(интервал) |
(–∞; a) |
−∞ < x < a |
(бесконечный |
|
|
интервал) |
(–∞; a] |
−∞ < x ≤ a |
(бесконечный |
|
|
полуинтервал) |

26 |
|
|
|
|
Функции, их свойства и графики |
||
[a; +∞) |
a ≤ x < +∞ |
|
|
|
|
|
(бесконечный |
|
|
|
|
||||
|
|
|
|
|
|
|
полуинтервал) |
(а; +∞) |
a < x < +∞ |
|
|
|
|
|
(бесконечный |
|
|
|
|
||||
|
|
|
|
|
|
|
интервал) |
(а – ε, а + ε) а – ε < x < а + ε |
|
|
|
|
|
(окрестностьточ- |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
киарадиусаε) |
Рис. 4
Принадлежность граничной точки промежутка этому промежутку обозначается на координатной прямой закрашенным кружочком. Незакрашенный кружочек обозначает точку, не принадлежащую промежутку.
Число b – а является длиной каждого из промежутков [a; b], [a; b), (a; b], (a; b).
Промежуток (а – ε, а + ε) называется окрестностью точки а радиуса ε > 0. Точка а является серединой этого промежутка, его длина равна 2ε.
Понятие модуля действительного числа, его геометрическая интерпретация широко применяются при решении разнообразных задач.
Òеîрема 3. Расстояниемеждуточкамикоординатнойпря-
мой равно модулю разности соответствующих им чисел.
Пусть даны точки А(х1), В(х2). Требуется доказать, что АВ =
=|х1 – х2|. Доказательство теоремы сводится к рассмотрению различных случаев размещения точек А(х1) и В(х2) на координатной прямой. Если х1 > 0, х2 < 0, (рис. 5, а), то АВ = АО + ОВ = х1 + (–х2) =
=х1 – х2 = = |х1 – х2|. Если х1 < 0, х2 < 0, |х1| < |х2|, то есть точка А расположена ближе к точке О, чем точка В (рис. 5, б), то АВ = BО –
–ОA = – х2 – (–х1) = х1 – х2 = |х1 – х2|. Аналогично рассматривают-
ся остальные случаи. Мы доказали, что модуль разности двух
чисел равен расстоянию между точками, изображающими данные числа.

Числовые множества |
27 |
Пользуясь понятиям модуля, легко записать некоторые геометрические утверждения в алгебраической форме. Например, «расстояние от точки х до точки 1 равно 2» означает, что |х – 1| = 2, а «расстояние от точки х до точки –1 меньше 3» — |х + 1| < 3.
Геометрическим смыслом модуля удобно пользоваться при решении простейших уравнений и неравенств, содержащих выражения с модулями.
Пример 6. Решить уравнение |х + 2| = 1.
Перепишем данное уравнение в виде |х – (–2)| = 1. Геометрически оно означает, 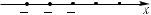 что расстояние от точки –2 до искомой точ-
что расстояние от точки –2 до искомой точ-
ки х равно 1. Откладывая на координат-  ной прямой (рис. 6) от точки –2 по обе стороны от нее отрезки длиной 1, получим: x1 = −3, x2 = −1.
ной прямой (рис. 6) от точки –2 по обе стороны от нее отрезки длиной 1, получим: x1 = −3, x2 = −1.
Ответ. – 3; – 1.
Пример 7. Решить неравенство: 1) x −5 ≤ 3; 2) |x + 2| > 1.
1) Геометрический смысл задания состоит в том, чтобы найти множество то- 
чек, удалённых от точки 5 на расстояние не больше 3. Изобразим эти точки на ри-
сунке (рис. 7). Запишем искомые точки в виде промежутка: [2; 8]. Решением неравенства являются точки отрезка [2; 8].
2) Неравенство можно переписать в
виде: |x – (–2)| > 1. Необходимо найти мно-  жество точек х, удалённых от точки –2 на расстояние, превышающее 1. Изобразим
жество точек х, удалённых от точки –2 на расстояние, превышающее 1. Изобразим 

 эти точки на рисунке (рис. 8). Решением
эти точки на рисунке (рис. 8). Решением
неравенства являются точки множества (–∞; –3) (–1; +∞).
Ответ. 1) [2; 8]; 2) (–∞; –3) (–1; +∞).
9 Контрольные вопросы
1°. Среди приведенных чисел укажите натуральные, целые, рациональные, иррациональные: (– 3)3; (– 3)2; 3,14; π; 64 ; 50 ;
4 ; |
9 ; 1,0(56). |
|
|
3 |
3 |
|
|
2°. Какие числа удовлетворяют уравнению: |
в) |x| = –4? |
||
а) |x| = 4; |
б) |x| = 0; |
||
28 |
|
|
|
|
|
|
|
|
|
Функции, их свойства и графики |
|||||||||||
3°. |
Какие из следующих чисел можно представить в виде периоди- |
||||||||||||||||||||
|
ческих десятичных дробей, а какие — в виде бесконечных непе- |
||||||||||||||||||||
|
риодическихдесятичныхдробей: |
2 |
; |
|
3; 3 ; 7; |
25; − |
12; − 6 ? |
||||||||||||||
|
|
|
|||||||||||||||||||
4°. |
|
|
|
|
|
|
|
11 |
|
|
8 |
|
|
|
|
17 |
|
|
|
||
Может ли произведение рациональных чисел быть иррацио- |
|||||||||||||||||||||
|
нальным числом? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5. |
Может ли произведение иррациональных чисел быть рацио- |
||||||||||||||||||||
|
нальным числом? |
|
|
|
|
|
|
правильно, если: |
|
|
|
||||||||||
6. |
Какое из равенств |х| = х или |х| = – х |
|
|
|
|||||||||||||||||
|
1) x = 2 −1; |
|
|
2) x = 3 − 2; |
|
|
|
|
|
|
|
|
|||||||||
|
3) x = 3 3 − 2 7; |
|
4) x = 3 2 − 2 5? |
|
|
|
|
|
|
|
|||||||||||
Задачи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1°. |
Представьте число в виде бесконечной десятичной дроби: |
||||||||||||||||||||
|
1) 5; |
|
|
|
2) 7 ; |
|
3) − 3 |
; |
4) |
7 . |
|
|
|
|
|
||||||
2. |
|
|
|
|
|
3 |
|
7 |
|
|
5 |
|
|
|
|
|
|||||
Представьте число в виде обыкновенной дроби: |
|
|
|
|
|
|
|
||||||||||||||
|
1°) 0,27; |
2) 0,2222...; |
3) 2,(31); |
|
|
|
4) 3,4(52). |
|
|
|
|
|
|
|
|||||||
3°. |
Сравните числа: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1°) |
11 |
|
и |
11 |
; 2°) − 6 |
и 5 ; |
3°) 3 |
|
и 5 ; |
4°) 0,58 и |
|
7 |
. |
|||||||
|
|
|
305 |
12 |
|||||||||||||||||
4. |
315 |
|
7 |
7 |
4 |
|
6 |
|
|
|
|
|
|
||||||||
Выполните действия и запишите результат в виде конечной |
|||||||||||||||||||||
|
или бесконечной десятичной дроби: |
|
|
|
|
|
|
|
|
|
|||||||||||
|
1) 5 + |
2; |
|
2) 1 + 0,25; |
3) |
5 |
|
3,15; |
4) |
|
2 |
|
:3,2. |
|
|
||||||
|
|
|
|
15 |
|
|
|
||||||||||||||
5. |
6 |
3 |
|
9 |
|
21 |
|
|
|
|
|
|
|
|
|||||||
Даны два рациональных числа: |
|
|
|
|
|
1 и |
2 . |
||||||||||||||
|
1) 0,53 и 0,64; |
2) –0,03 и 0,03; 3)0,3462и0,3463; |
4) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
7 |
|
|
Укажите по крайней мере одно рациональное число, содержа- |
||||||||||||||||||||
|
щееся между ними. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6.Назовите несколько положительных значений переменной а,
при которых значение выражения a является:
1) иррациональным числом; 2) рациональным числом.
7°. На рис. 9 изображены числовые множества. Запишите заданные множества в виде числовых промежутков.
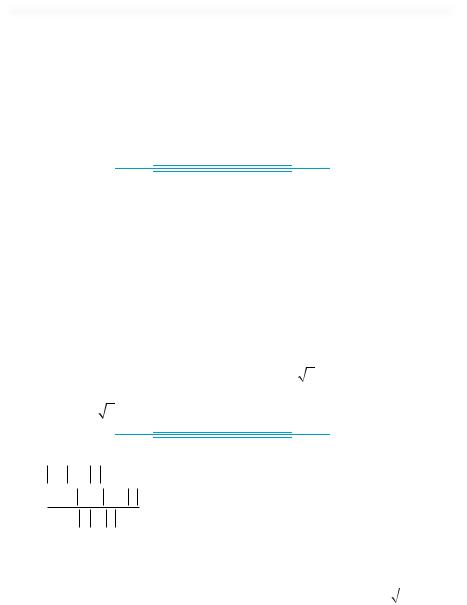
Числовые множества |
29 |
8°. Изобразите на координатной прямой числовые множества:
1) (3; 4); |
2) [– 2; 1); 3) [–2; –1]; 4) |
(−∞; −2] |
; 5) 1;+∞ |
) |
. |
|
|
[ |
|
9°. Изобразите на координатной прямой множество точек, координаты которых удовлетворяют условию:
1) 1< x <2; 2) 1 ≤ x ≤ 3; 3) – 1 < x ≤ 1; 4) x > 4; 5) х ≤ –3.
10°.Запишите в виде неравенства с модулем двойное неравенс- |
||
тво: |
2) –1 < х < 3; |
3) –5 < х < 3. |
1) –2 < х < 2; |
||
11.Даны точки А(3) и В(5). Найдите координаты точки:
1)симметричной точке А относительно В;
2)симметричной середине отрезка АВ относительно точки В.
12.Для каждого из следующих интервалов укажите его длину и координату его середины:
1) (1,3; 2,56); |
2) (−π;2π); |
3) (–2,13; 2,15). |
13.Изобразите на координатной прямой множество точек, координаты которых удовлетворяют условию:
1) |
|
x |
|
= 3; |
|
2) |
|
x |
|
≤ 3; |
3) |
|
x |
|
> 3; |
4) |
|
x |
|
> −3; 5) |
|
x |
|
< −3. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
14. Найдите |x|, если: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1) |
x = 7 − |
8 |
; |
|
|
|
|
2) |
x = 3 − 8 ; |
|||||||||||||||
|
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3) |
x = 4 −3 |
2 ; |
|
|
|
|
4) |
x = 2,(251)−2,25(1). |
||||||||||||||||
15.Вычислите значение выражения:
1)−a −2 b , если a = −1,b = −2 ;
2)−1 − −3a + 4 b , если a = −4,b = 0. 2 a + b
16.Решите уравнение:
1) |
|
2x +1 |
|
= 3 ; 2) |
|
2−4x |
|
=1 ; 3) |
|
2x −5 |
|
= −2; 4) |
|
x + 2 |
|
= x + 2 . |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||
17. Решите неравенство: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1) |
|
x +3 |
|
> 2; |
|
2) |
|
4x −1 |
|
<1 ; |
|
|
|
3) |
|
x −2 |
|
<1− 2 . |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
18*.Сравните значение выражений: |
|
|
|
3) |a2| и а2. |
||||||||||||||||||||||
1) |
|a| и а; |
|
2) –|a| и а; |
|
|
|
||||||||||||||||||||
30 Функции, их свойства и графики
Упражнения для повторения
19. |
Запишите в виде обыкновенной дроби: |
|
|
||||
|
1) 6%; |
2) 18%; 3) |
2 %; |
4) 3 |
3 %; |
5) 112 |
1 %; 6) 350%. |
20. |
Выразите в процентах: |
3 |
|
4 |
|
2 |
|
|
|
|
|
|
|||
1) 0,08; 2) 0,6; 3) 2; 4) 3,2; 5) 0,0043.
21.На сколько процентов увеличится площадь круга, если его радиус увеличить на 20%?
22.Богдан и Гриша играли в одной баскетбольной команде. Богдан за игру 20 раз бросал мяч в корзину, при этом 15 раз его броски были меткими. Гриша сделал 25 бросков, из которых 18 оказались меткими. Кто из них был более метким в этой игре?
Итог
Основные понятия
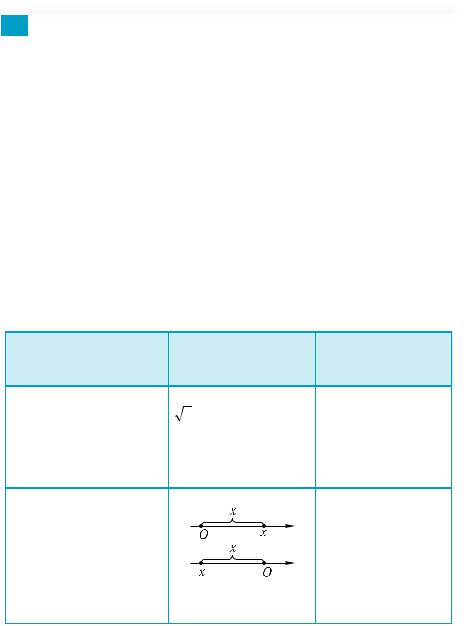
|
Геометрическая |
|
|
|
||
Определение |
интерпретация, |
Применение |
||||
|
примеры |
Иррациональные |
||||
Иррациональным чис- 0,35355355535555..., |
||||||
лом называется беско- |
2 = 1,41421356..., |
числа |
дают воз- |
|||
нечная десятичная не- |
π = 3,1415926535... . |
можностьизмерять |
||||
периодическая дробь. |
|
|
|
длины |
|
отрезков, |
|
|
|
|
несоизмеримых с |
||
Расстояние от начала |
|
|
|
единичным. |
||
|
|
|
Понятие |
модуля |
||
координат О до точки |
|
|
|
числа |
позволяет |
|
х называется модулем |
|
|
|
записывать с помо- |
||
числа х и обозначается |
|
|
|
щью |
выражений |
|
|
|
|
||||
|х|. |
|
|
|
взаимное |
распо- |
|
|
|
|
|
ложение точек на |
||
координатной прямой.

Числовые множества |
31 |
Основные утверждения |
|
Содержание утверждения |
Примеры |
Каждое рациональное число m можно
представить в виде десятичнойnпериодической дроби.
Каждая десятичная периодическая дробь изображает определенное рациональное число.
Каждому действительному числу соответствует единственная точка координатной прямой, и наоборот, каждая точка координатной прямой соответствует единственному действительному числу.
Расстояние между точками координатной прямой равно модулю разности соответствующих им чисел.
53 =1,6666... =1,(6).
 3,(7) = 3 79 .
3,(7) = 3 79 .
