
- •Обращение к читателю
- •Введение
- •РАЗДЕЛ 1. Функции, их свойства и графики
- •§1. Числовые множества
- •§2. Вычисления и расчёты
- •§3. Функциональные зависимости
- •§4. Основные свойства функций
- •§5. Корни n-ой степени
- •§6. Степенные функции с рациональными показателями
- •§7. Основные понятия и аксиомы стереометрии
- •§8. Взаимное расположение двух прямых в пространстве
- •§9. Параллельное проектирование
- •§10. Изображение фигур в стереометрии
- •§11. Параллельность прямых и плоскостей
- •§12. Параллельность плоскостей
- •§13. Тригонометрические функции числового аргумента
- •§14. Основные соотношения между тригонометрическими функциями
- •§15. Свойства и графики тригонометрических функций
- •§16. Тригонометрические формулы сложения и следствия из них
- •§17. Простейшие тригонометрические уравнения и неравенства
- •§18. Перпендикулярность прямой и плоскости
- •§19. Связь между параллельностью и перпендикулярностью прямых и плоскостей
- •§20. Перпендикулярность плоскостей
- •§21. Ортогональное проектирование
- •§23. Измерение расстояний в пространстве
- •§24. Измерение углов в пространстве
- •Ответы и указания к задачам
- •Предметный указатель
- •Содержание

§10. изображение фигур в стереометрии
Ðассматриваются особенности построения изображений фигур, в первую очередь плоских, задачи на построение на изображениях.
При изучении вопроса об изображении фигур в 
 стереометрии основное внимание сосредоточим на
стереометрии основное внимание сосредоточим на  изображении плоских фигур. И это понятно, поскольку глядя на реальный физический объект (дом, игральный кубик, книгу и др.), мы видим поверхность, во многих случаях состоящую из плоских частей (рис. 201 – 203). На рисунках и технических чертежах прежде всего пытаются изобразить поверхность объекта, а наш жизненный опыт дает возможность за деталями поверхности увидеть предмет в целом.
изображении плоских фигур. И это понятно, поскольку глядя на реальный физический объект (дом, игральный кубик, книгу и др.), мы видим поверхность, во многих случаях состоящую из плоских частей (рис. 201 – 203). На рисунках и технических чертежах прежде всего пытаются изобразить поверхность объекта, а наш жизненный опыт дает возможность за деталями поверхности увидеть предмет в целом.
Поскольку основная геометрическая фигура — это треугольник, выясним, какая фигура может быть изображением треугольника. А затем мы сможем обсудить вопрос об изображении других многоугольников,известныхизпланиметрии.Крометого,речьбудетидти и об изображении простейших пространственных фигур.
За геометрическую основу изображения возьмем параллельное проектирование. Прежде всего нужно уточнить содержание понятия «изображение», ведь понимать под изображением фигуры непосредственно ее параллельную проекцию — достаточно
Изображение фигур в стереометрии |
185 |
неудобно. Фигуру больших размеров просто невозможно спроектировать на лист бумаги — для того, чтобы изображение поместилось, параллельную проекцию фигуры нужно пропорционально уменьшить (или увеличить в других ситуациях).
Изображением пространственной фигуры называется фигура, подобная параллельной проекции данной фигуры на некоторую плоскость.
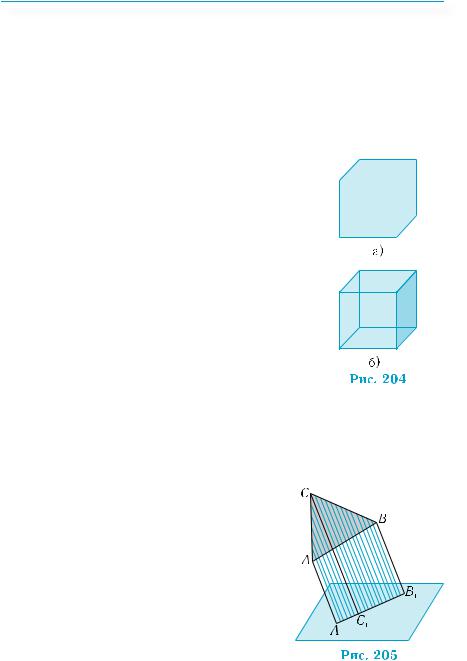
Данное определение требует дополнения. Понятно, что изображение должно содержать как можно больше информации о фигуре. Вряд ли параллельная проекция куба на рис. 204, а) достаточно полно отображает особенности этой фигуры. Поэтому
на изображении многогранников изображают их вершины и рёбра, видимые и невидимые.Какужеотмечалось,невидимыелинии изображают штриховыми линиями. Таким образом, изображение куба на рис. 204, б)
даёт более полную информацию о кубе. На изображении пространственной фи-
гуры выделяют также изображения ее важных элементов (например, диагоналей, сечений и т. п.).
Отметим, что в определении не фиксируется ни плоскость проекций, ни направление проектирования. Это и понятно, поскольку удобную для рассмотрения позицию можно выбирать произвольно.
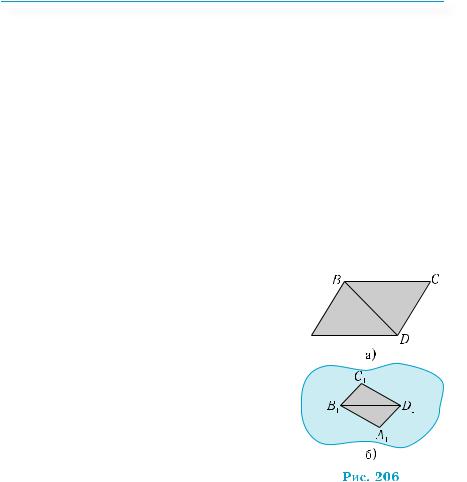
Теперь ответим на вопрос: какая фигура может быть изображением треугольника? Случай, когда треугольниклежитвпроектирующейплоскос-
ти, не будем рассматривать. В этом случае он проектируется на отрезок (рис. 205).
Поскольку параллельной проекцией треугольника является треугольник (кроме отмеченного выше случая), то и изображением треугольника должен быть тре-
угольник. В то же время возникает вопрос: «А какой треугольник можно считать изображением данного треугольника?» Как известно, при параллельном проекти-
186 |
Параллельность прямых и плоскостей |
ровании изменяются длины отрезков, меры углов. Понятно, что параллельной проекцией равнобедренного треугольника является, вообще говоря, разносторонний треугольник, проекцией тупоугольного треугольника может быть остроугольный и т. д.
Проведение простых экспериментов с картонными моделями треугольников при получении их тени от Солнца или от удаленной лампы показывает, что форма параллельных проекций треугольника может быть различной. Более того, можно убедиться в том, что за счет соответствующего размещения модели можно получить в качестве проекции треугольник заданной формы. Таким образом, рассматривая различные тени одного треугольника, можно прийти к следующему выводу.
Изображением данного треугольника может быть произвольный треугольник.
Математическое обоснование этого факта будет сделано позже. Пользуясь им, можно сделать определенные выводы относительно изображения некоторых четы-
рехугольников. 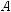 Из свойств параллельного проектиро-
Из свойств параллельного проектиро-
вания вытекает, что изображением параллелограмма является произвольный
параллелограмм. Действительно, параллелограмм диагональю разбивается на два равных треугольника (рис. 206, а). Изоб-
ражением треугольника ABD может быть произвольный треугольник A1B1D1. Достро-
ив треугольник A1B1D1 до параллелограм-
ма (рис. 206, б), который однозначно определяется этим треугольником, получим следующий вывод.
Изображениямданногопараллелограммаможетбыть произвольный параллелограмм.
Относительнотрапецийподобныйвыводобихизображенияхсделать нельзя, поскольку при параллельном проектировании должно сохраняться отношение длин параллельных оснований. Если, например, одно из оснований вдвое меньше второго, то и на изображении это соотношение должно сохраняться. Хотя, конечно, изображением трапеции должна быть трапеция (но не произвольная!).
Изображение фигур в стереометрии |
187 |
Что касается изображения других многоугольников, то можно выбрать три их точки, не лежащие на одной прямой (например, три вершины). Эти точки определяют треугольник, который может изображаться произвольным треугольником. Далее, пользуясь свойствами параллельного проектирования (они являются и свойствами изображений), можно в некоторых случаях строить изображение всего многоугольника.
Научившись изображать некоторые плоские фигуры, размещенные в пространстве, можем приступить к изображению простейших пространственных фигур.
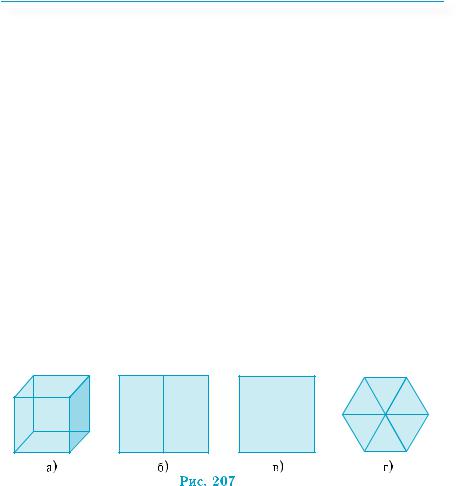
Изображения прямоугольного параллелепипеда, куба ничем не отличаются от изображений произвольного параллелепипеда, так как изображениями квадратов и прямоугольников могут быть произвольные параллелограммы. Чаще всего куб изображают так, как это сделано на рис. 207, а). На рис. 207, б)–г) также даны изображения куба. Однако, в отличие от рис. 207, а), по этим изображениям трудно составить представление о свойствах куба. На рис. 207, б), в) изображения простые и правильные, то есть выполнены по законам параллельного проектирования. Однако они не являются наглядными. Сказанное не означает, что в некоторых случаях нам не понадобится каждое из приведенных изображений.
Рассмотрим подробнее построение изображения параллелепипеда. В §7 параллелепипед рассматривался как многогранник, гранями которого служат шесть параллелограммов. В §8 рассматривался подход к построению фигур из отрезков. Воспользуемся
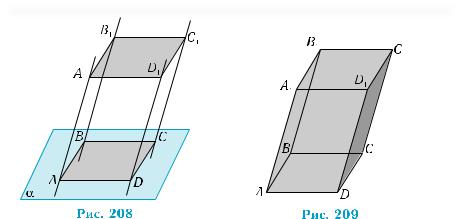
им.В данной плоскости α построим параллелограмм АВСD и через все его вершины проведем параллельные прямые, пересекающие плоскость α (рис. 208). На этих прямых по одну сторону от плоскости α отложим отрезки АА1, ВВ1, СС1, DD1 одинаковой длины. Нетрудно доказать, что точки А1, В1, С1, D1 лежат в одной плоскости и являются вершинами параллелограмма А1B1C1D1. Действи-
188 |
Параллельность прямых и плоскостей |
тельно, поскольку АA1D1D, АВСD и ВB1C1C — параллелограммы, то А1D1 || AD, AD || ВС, ВС || В1C1 и, согласно признаку параллельности прямых (теорема 2 §8), А1D1 || В1C1. Это, в частности, дает нам возможность утверждать, что точки А1, В1, С1, D1 лежат в одной плоскости.
Аналогично имеем, что А1B1 || D1C1, то есть четырехугольник А1B1C1D1 является параллелограммом.
Совокупность всех точек отрезков, соединяющих точки параллелограммов ABCD и А1B1C1D1, образуют фигуру, являющуюся параллелепипедом (рис. 209). Понятно, что при построении параллелепипедов можно обойтись параллельными отрезками, соединяющими соответствующие точки параллелограммов. Изображение выполнено, как и на рис. 208, только с учетом того, что параллелепипед «заполнен» точками, и некоторые линии невидимы для наблюдателя. Как и в черчении, их изображают штриховой линией. Обозначают параллелепипед по его вершинам:
ABCDА1B1C1D1.
Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общего ребра, - противоположными. Две вершины, не принадлежащие к одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллеле-
пипеда.
Изображение пирамид, в частности тетраэдров, было рассмотрено в §8 в связи с их построением из отрезков.
Изображение фигур в стереометрии |
189 |
!Рассмотрение изображений плоских и пространствен-
ных фигур позволяет сформулировать требования к изображениям:
1)изображение должно быть правильным, то есть удовлетворять определенным правилам;
2)изображение должно быть наглядным;
3)изображение должно быть простым для выполнения.
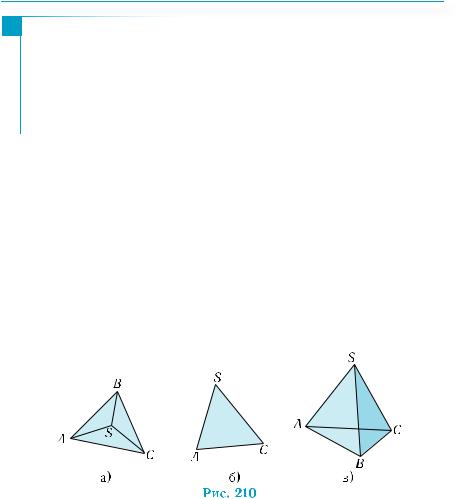
Правильность изображения обеспечивается соблюдением правил построения параллельных проекций. Наглядность и простота обеспечиваются выбором направления проектирования, то есть «угла зрения» на фигуру и расположением плоскости проекции. Так, изображения тетраэдра SABC на рис. 210, а), б) нельзя считать удачными. В первом случае использовано параллельное проектирование на плоскость грани АВС, а во втором — направление проектирования определяется прямой АВ. В обоих этих случаях потеряна объемность фигуры. Как правило, используют третье изображение (рис. 210, в). Оно является плоским четырехугольником ABCS, в котором проведены диагонали АС и SB. Невидимое ребро АС изображено штриховой линией.
Важным средством обеспечения наглядности изображения является изображение элементов фигуры (медиан, биссектрис, средних линий, диагоналей и т. п.), а также простейших сечений.
Построение изображений различных фигур является неотъемлемой составляющей решения задач стереометрии.
Часто при решении задач необходимо выполнить определенные построения на изображении (провести медиану, указать центр вписанной окружности, построить сечение и т. п.). Эти построения обычно выполняются по свойствам параллельного проектирования.
190 |
Параллельность прямых и плоскостей |
Пример 1. На произвольном изображении прямоугольного равнобедренного треугольника АВС ( С = 90°) построить изображение: 1) центра О описанной окружности; 2) вписанного квадрата, две стороны которого лежат на катетах
треугольника, а одна из вершин — на гипотенузе ВА.
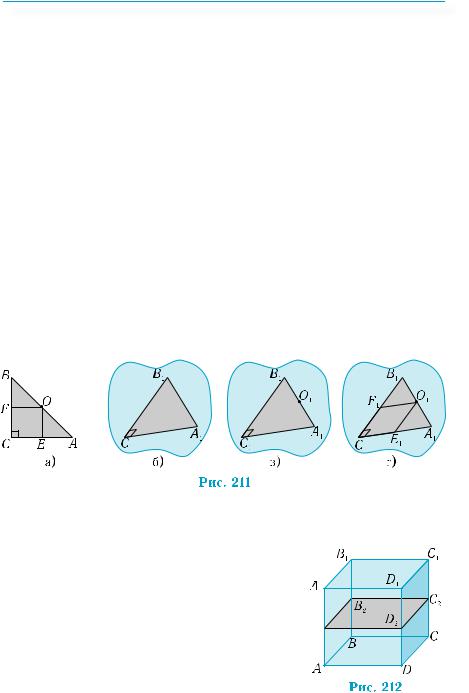
Пусть изображением прямоугольного равнобедренного треугольникаАВС(рис.211,а)являетсятреугольникА1В1С1 (рис.211,б).
1) Центр описанной около прямоугольного треугольника окружности является серединой гипотенузы. Поэтому его изображение является серединой изображения гипотенузы.
Построение. Разделим отрезок А1В1 пополам, точка деления О1 и является искомой (рис. 211, в).
2)ЕслиизсерединыОгипотенузыАВпровестиперпендикуляры к катетам (см. рис. 211, а), то получим квадрат, удовлетворяющий условию задания. Проведенные перпендикуляры параллельны катетам. Именно этим воспользуемся для построения искомого изображения.
Построение. Из точки О1 проводим отрезки О1Е1 и О1F1, параллельные С1В1 и С1А1 соответственно (рис. 211, г). Четырехугольник С1Е1О1F1 является искомым.
Пример 2. На изображении куба построить его сечение плоскостью, проходящей через середины трех параллельных рёбер.
На рис. 212 середины ребер АА1, ВВ1, СС1, DD1 куба АBCDA1B1С1D1 обозначены соответственно через А2, В2, С2, D2. Изображения этих точек лежат на серединах изоб- 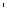 ражений соответствующих отрезков (почему?). Пусть секущая плоскость проходит
ражений соответствующих отрезков (почему?). Пусть секущая плоскость проходит  через точки А2, В2, D2. Поскольку все грани куба — квадраты, то отрезок А2В2, проходящий через середины противоположных
через точки А2, В2, D2. Поскольку все грани куба — квадраты, то отрезок А2В2, проходящий через середины противоположных

Изображение фигур в стереометрии |
191 |
сторон квадрата АА1В1В, равен стороне квадрата АВ (или ребру куба) и параллелен этой стороне.
Аналогично D2C2 || DС и D2C2 = DС. Поскольку и АВ || DС, то, в соответствии с транзитивностью отношения параллельности, А2В2 || D2C2. Через параллельные прямые А2В2, D2C2 проходит единственная плоскость. В этой плоскости лежат точки А2, В2, D2, поэтому данная плоскость является искомой секущей. Секущая плоскость пересекает грани куба по равным отрезкам А2В2, В2С2, С2D2 и D2A2. Следовательно, четырехугольник А2В2С2D2, являющийся искомым сечением, имеет форму ромба. Нетрудно заметить, что диагонали В2D2 и А2С2 этого ромба равны между собой. То есть четырехугольник А2В2С2D2 — квадрат. Мы не только построили сечение, но и установили его форму.
Рассмотрим обоснование приведенных выше выво- 
 дов относительно изображения основных плоских
дов относительно изображения основных плоских  фигур.
фигур.
Теорема 1 (об изображении треугольника).
Любой треугольник может быть изображением данного треугольника.
Пусть дан треугольник АВС. Возьмем произвольный треугольник KМN. Он может быть изображениям треугольника АВС, если существуют плоскость проекций и направление проектирования такие, что параллельная проекция треугольника АВС подобна треугольнику KМN.
Выберем плоскость проекций α так, чтобы она пересекала плоскость треугольника АВС по прямой АС (рис. 213). Нам нужно выбрать направление проектирования так, чтобы проекцией треугольника АВС на плоскость α был треугольник, подобный треугольнику KМN. Для этого построим в плоскости α треугольник САЕ, подобный треугольнику KМN с коэффициентом подо-
бия MKAC

192 |
Параллельность прямых и плоскостей |
рования. Поскольку треугольник САЕ является параллельной проекцией треугольника АВС, а треугольники САЕ и KМN — подобны, то треугольник KМN является изображением треугольни-
ка АВС.
!Эта теорема открывает широкие возможности для выбора изображений данного треугольника, хотя, конечно, не стоит использовать изображения со свойствами, которыми не обладает оригинал. Например, нецелесообразно изображать произвольный треугольник в виде прямоугольного.
Переходя к изображениям других многоугольников, заметим, что для них, как правило, теоремы, аналогичные теореме 1, не имеют места, хотя отдельные их свойства сохраняются при изображении. Прежде всего речь будет идти о параллельности сторон (почему?). В связи с этим приведем еще одну важную теорему.
Теорема 2 (об изображении параллелограмма).
Любой параллелограмм может быть изображением данного параллелограмма.
Доказать эту теорему можно, разбив параллелограммы диагоналями на треугольники и воспользовавшись теоремой 1 (см.
рис. 206, а, б)
Мы уже встречались с ситуациями, когда планиметрические факты имеют аналоги в пространстве. И такие случаи будут встречаться и дальше. Самой простой пространственной фигуре — тетраэдру — соответствует на плоскости треугольник. По теореме 1, любой треугольник может быть изображением данного треугольника. С другой стороны, тетраэдр проектируется в четырехугольник, который после проведения в нем диагоналей становится изображением тетраэдра. Возникает вопрос: может ли произвольный четырехугольник быть изображением данного тетраэдра? Утвердительный ответ на него дает теорема немецких математиков Польке К. (1810–1877) и Шварца Г. (1843–1921). Исходя из нее, можно строить изображение многогранников. Для этого нужно выбрать четыре вершины, не лежащие в одной плоскости. Они являются вершинами некоторого тетраэдра. Потом задать произвольным образом изображение этих точек. А уже тогда достраивать изображение всей фигуры, пользуясь свойствами проектирования.
Изображение фигур в стереометрии |
193 |
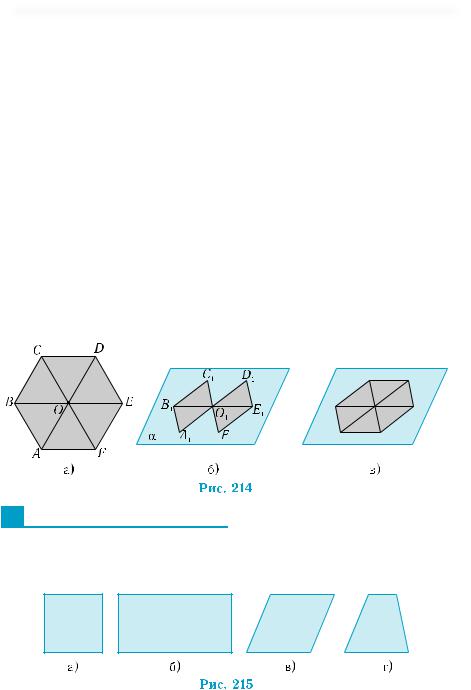
Пример 3. Построить изображение правильного шестиугольника.
РассмотримправильныйшестиугольникАВСDЕF(рис.214,а). Он обладает свойствами, которые должны сохраняться в его изображениях. Стороны шестиугольника попарно параллельны (АВ || ЕD, ВС || ЕF, СD || АF). Он имеет центр симметрии О, а отрезки, соединяющие точку О с вершинами шестиугольника, равны между собой и равняются его стороне. Теперь нетрудно заметить, что достаточно построить изображение параллелограмма (даже ромба) АВСО, чтобы потом достроить к нему изображение всего шестиугольника.
Пусть параллелограмм А1В1С1О1 является изображением параллелограмма АВСО (это может быть произвольный параллелограмм!). Продлив А1О1 и С1О1 за точку О1 так, чтобы О1D1= А1O1, О1F1 = С1O1, построим параллелограмм F1О1D1E1 (рис. 214, б). По существу, построен параллелограмм, центрально-симметричный параллелограмму А1В1С1О1 относительно его вершины О1. Соединив точки А1 и F1, С1 и D1, получим изображение правильного шестиугольника (рис. 214, в).
Контрольные вопросы
1.Какая из фигур на рис. 215, а)–г) не является изображением квадрата?
194 |
Параллельность прямых и плоскостей |
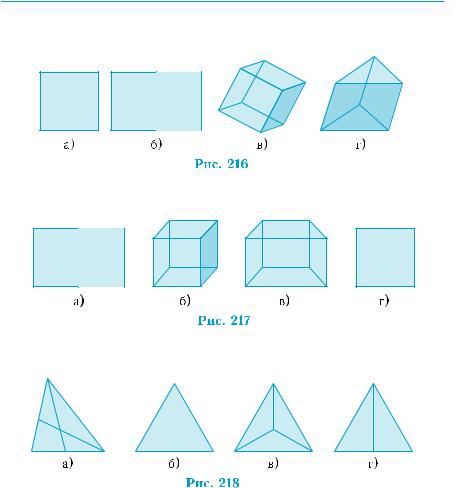
2.Какая из фигур на рис. 216, а)–г) не является изображением куба?
3.На каком из рис. 217, а)–г) изображение куба не является правильным?
4.На каком из рис. 218, а)–г) изображение тетраэдра не является правильным?
5.Являетсялипараллельнаяпроекцияфигурыееизображением?
6.Можно ли прямоугольный треугольник считать изображением равнобедренного треугольника?
7.Верно ли, что изображением средней линии треугольника является средняя линия его изображения?
8.Может ли параллелограмм быть изображением трапеции?
9.Может ли треугольник быть изображением тетраэдра?
10.Можно ли тетраэдр изобразить так, чтобы ровно одна его грань была невидимой?
Изображение фигур в стереометрии |
195 |
11.Какое наименьшее количество рёбер куба может быть видимыми при изображении? А наибольшее?
12.Какой фигурой является изображение: а) отрезка; б) треугольника; в) трапеции; г) параллелограмма; д) п-угольника?
Графические упражнения
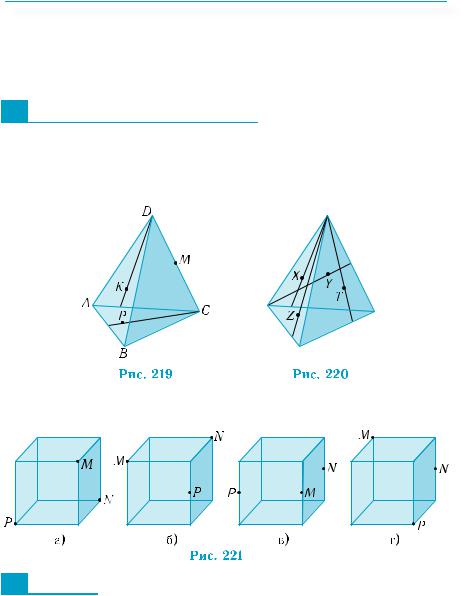
1.Установите, каким граням тетраэдра ABCD, изображенного на рис. 219, принадлежат точки Р, K, М?
2.Какие пары из точек X, Y, Z, Т, указанных на изображении тетраэдра на рис. 220, не лежат в одной грани?
3.Какой фигурой является сечение куба плоскостью, проходящей через точки М, N, Р, указанные на рис. 221, а)–г)?
Задачи
174°. Дано изображение равнобедренного треугольника в виде разностороннего треугольника. На этом изображении постройте изображение:
1) биссектрисы угла при вершине;

196 |
Параллельность прямых и плоскостей |
2) перпендикуляра к основанию, проведенного через середину боковой стороны; 3) ромба, две смежные стороны которого совпадают с боко-
выми сторонами треугольника.
175. Наизображенииравнобедренногопрямоугольноготреугольника постройте изображение квадрата, лежащего в плоскости треугольника, если стороной квадрата является:
1°) катет данного треугольника; 2) гипотенуза данного треугольника.
176. На произвольном изображении равностороннего треугольника АВС постройте изображение:
1°) точки пересечения высот треугольника; 2°) «описанного» прямоугольника, одна из сторон которого
совпадает с некоторой стороной треугольника, а другая содержит противоположную вершину; 3) биссектрисы внешнего угла треугольника.
177. Дано изображение треугольника и двух его высот. Постройте изображение центра окружности, описанной около этого треугольника.
178. На изображении прямоугольного треугольника, один из острых углов которого равен 60°, постройте изображение: 1) биссектрисы этого угла; 2) высоты, проведенной к гипотенузе;
3) центра вписанной окружности.
179°. Постройте изображение ромба и его высоты, проведенной из вершины угла, величина которого составляет 120°.
180. Постройте изображение квадрата, имея изображение точки пересечения его диагоналей и двух:
1°) соседних вершин; 2*) противоположных вершин. 181. На произвольном изображении равнобокой трапеции, боковая сторона которой равна меньшему основанию, постройте
изображение:
1°) оси симметрии трапеции; 2) вписанного прямоугольника, две вершины которого ле-
жат на большем основании и одна из сторон совпадает с меньшим основанием; 3) центра окружности, касающейся боковых сторон и мень-
шего основания трапеции.
182. Дано изображение равнобокой трапеции, углы при основании которой равны 45°. Постройте изображение:

Изображение фигур в стереометрии |
197 |
1) центра окружности, описанной около трапеции;
2*) центра окружности, касающейся меньшего основания и боковых сторон.
183. Дано изображение окружности и одного из его диаметров. Постройте изображение радиусов окружности, перпендикулярных этому диаметру.
184. Дано изображение куба АВСDА1В1С1D1.
1°) Постройте линию пересечения плоскостей DА1С1 и В1D1D. 2) Найдите длину отрезка этой линии, содержащегося в кубе, если ребро куба равно а.
3) Постройте сечение куба плоскостью, проходящей через центры трех попарно смежных его граней.
185. Дано изображение тетраэдра АВСD, точки K, М и Р — середины DС, АD и ВD, соответственно.
1°) Постройте линию пересечения плоскостей АСР и ВМK. 2) Найдите длину отрезка этой линии, содержащегося в тетраэдре, если длины всех его рёбер равны а.
3) Постройте сечение тетраэдра плоскостью, проходящей через точки пересечения медиан трех его граней.
186. Постройте сечение тетраэдра SABC плоскостью, проходящей через:
1°) середины рёбер SA, SC и BC;
2) точку M на AS (AM : AS = 1:2), точку N на SC (CN : NS = 1:2)
и точку P на BC (CP : PB = 1:2);
3) середины рёбер AS, AB и центр грани SBC; 4*) центры граней ASB, ABC и BSC.
187. Постройте сечение куба АВСDА1В1С1D1 плоскостью, проходящей через:
1) ребро CD и центр грани AA1B1B;
2) диагональ A1D и центр грани ВСС1В1;
3*) середины рёбер AD, CD и точку В;
4*) центры граней CDD1C1, СВВ1С1 и точку А.
Упражнения для повторения
188.Две параллельные прямые пересечены третьей прямой. Один из восьми образовавшихся углов равен 50°. Чему равняется каждый из остальных углов?
198 |
Параллельность прямых и плоскостей |
189. Дан куб АВСDА1В1С1D1.
1) Укажите все рёбра, параллельные ребру AA1.
2) Докажите, что ребро DC параллельно пересечению плоскостей ABC1 и A1B1D.
3) Существует ли в плоскости ABC1 прямая, параллельная прямой A1D1?
4) Пусть а — произвольный отрезок в грани куба. Постройте отрезок, параллельный отрезку а, в несмежной грани куба.
Итог
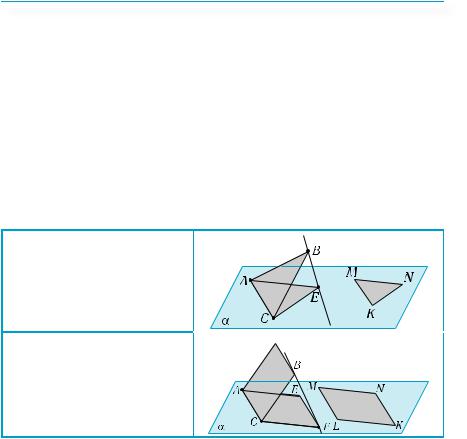
Основные утверждения |
Любой треугольник может |
быть изображением данно- |
го треугольника. |
Любой параллелограмм может быть изображением данного параллелограмма.
может быть изображением данного параллелограмма. 
