
- •Обращение к читателю
- •Введение
- •РАЗДЕЛ 1. Функции, их свойства и графики
- •§1. Числовые множества
- •§2. Вычисления и расчёты
- •§3. Функциональные зависимости
- •§4. Основные свойства функций
- •§5. Корни n-ой степени
- •§6. Степенные функции с рациональными показателями
- •§7. Основные понятия и аксиомы стереометрии
- •§8. Взаимное расположение двух прямых в пространстве
- •§9. Параллельное проектирование
- •§10. Изображение фигур в стереометрии
- •§11. Параллельность прямых и плоскостей
- •§12. Параллельность плоскостей
- •§13. Тригонометрические функции числового аргумента
- •§14. Основные соотношения между тригонометрическими функциями
- •§15. Свойства и графики тригонометрических функций
- •§16. Тригонометрические формулы сложения и следствия из них
- •§17. Простейшие тригонометрические уравнения и неравенства
- •§18. Перпендикулярность прямой и плоскости
- •§19. Связь между параллельностью и перпендикулярностью прямых и плоскостей
- •§20. Перпендикулярность плоскостей
- •§21. Ортогональное проектирование
- •§23. Измерение расстояний в пространстве
- •§24. Измерение углов в пространстве
- •Ответы и указания к задачам
- •Предметный указатель
- •Содержание

§19. связь между параллельностью и перпендикулярностью прямых и плоскостей
Äанный параграф посвящен установлению связей между параллельностью и перпендикулярностью прямых и плоскостей, широко применяемых в геометрии и ее приложениях.
 О существовании связей между параллельностью и
О существовании связей между параллельностью и
 перпендикулярностью в пространстве свидетельствует наш опыт. Действительно, столбы, установленные вертикально, параллельны между собой (рис. 394); параллельны вертикально направленные ледовые сосульки (рис. 395), вертикаль-
перпендикулярностью в пространстве свидетельствует наш опыт. Действительно, столбы, установленные вертикально, параллельны между собой (рис. 394); параллельны вертикально направленные ледовые сосульки (рис. 395), вертикаль-
ные колонны, украшающие сооружения (рис. 396), и т. п.
Хорошо известно содержание аналогичных связей в планиметрии: два перпендикуляра к одной прямой параллельны между собой, и наоборот, прямая, перпендикулярная одной из двух параллельных прямых, перпендикулярна и второй. Однако для прямых в пространстве эти утверждения не всегда выполняются (попробуйте сами привести соответствующие примеры). Вместе с тем можно изучать ситуации, связанные с параллельностью и перпендикулярностью прямых и плоскостей в пространстве.
Рассмотрим детальнее связь между параллельностью прямых и перпендикулярностью их плоскости. Эти связи отражают отношения между реальными объектами, которыми мы пользу-
390 |
Перпендикулярность прямых и плоскостей |
|
емся в повседневной жизни. Действительно, |
|
|
|
если одна доска забора расположена верти- |
|
кально, то вторую доску достаточно располо- |
|
жить параллельно первой, чтобы она также |
|
была вертикальной (рис. 397). Этот способ |
|
построения забора основывается на следую- |
|
щей теореме. |
|
|
Теорема 1 (о двух параллельных прямых, одна из которых перпендикулярна плоскости).
Если одна из двух параллельных прямых перпендикулярна плоскости, то и вторая прямая перпендикулярна этой плоскости.
Приведенная теорема является признаком перпендикулярнос- ти прямой и плоскости, то есть с ее помощью устанавливают пер- пендикулярность прямой и плоскости. Её широко используют не только в геометрии, но и в практической деятельности. Сооружение стен здания с 

использованием отвеса является яркой ил- 





 люстрацией применения этого признака
люстрацией применения этого признака  перпендикулярности прямой и плоскости.
перпендикулярности прямой и плоскости.  Действительно, нить отвеса расположена
Действительно, нить отвеса расположена  вертикально, и если кромка сооружения
вертикально, и если кромка сооружения 

















 параллельна нити, то она также верти- кальна (рис. 398).
параллельна нити, то она также верти- кальна (рис. 398). 
Рассмотрение теоремы 1 естественно порождает вопрос: будут ли параллельны две прямые, перпендикулярные одной плоскос- ти? Ответ на него нам подсказывает опыт (два вертикально уста- новленных столба — параллельны!), и он подтверждается следу- ющей теоремой, обратной теореме 1.
Теорема 2 (о параллельности прямых, перпендикулярных плоскости).
Еслидве прямые перпендикулярны однойитойжеплоскости, то они параллельны.
Приведенная теорема также является признаком. С её помо- щью устанавливают параллельность прямых в пространственных конструкциях. Ведь вертикальность или перпендикулярность

Связьмеждупараллельностьюиперпендикулярностьюпрямыхиплоскостей 391
плоскости иногда более легко проверить (особенно на громоздких объектах), чем параллельность. Речь идет, например, о располо- жении поперечных балок при сооружении потолка здания, рас- познавании параллельности прямых в геометрических конфигу- рациях и др.
Не менее важными в геометрии и ее приложениях являются связи между параллельностью плоскостей и их перпендикуляр- ностью прямой. Речь идёт о двух плоскостях и одной прямой. Если две плоскости параллельны и одна из них перпендикулярна прямой, то как будет расположена вторая плоскость по отноше- нию к этой прямой? Как расположены две плоскости, если они обе перпендикуляр-
ны прямой? Ответы на эти вопросы также нам подсказывает опыт практической деятельности. Если вбить гвоздь в доску перпендикулярно одной стороне доски, то он будет перпендикулярен и противопо- ложной (рис. 399). Если на ось колесной пары насадить колеса с обеих сторон так, чтобы их плоскости были перпендикуляр- ными оси, то плоскости этих колес будут параллельны (рис. 400).
Сформулируем два взаимно обратных утверждения, отражаю- щие связь между параллельностью плоскостей и их перпендику- лярностью прямой.
Теорема 3 (о параллельных плоскостях, одна из которых пер- пендикулярна прямой).
Если одна из двух параллельных плоскостей перпендикулярна прямой, то и вторая плоскость перпендикулярна этой же прямой.
Теорема 4 (о двух плоскостях, перпендикулярных прямой).
Если две плоскости перпендикулярны одной прямой, то они параллельны.
Привлекает внимание родство приведенных двух пар теорем. Каждую из них можно сформулировать, заменив термин «пря- мая» на «плоскость», и наоборот.
Теоремы 3 и 4 также являются признаками.
392 Перпендикулярность прямых и плоскостей
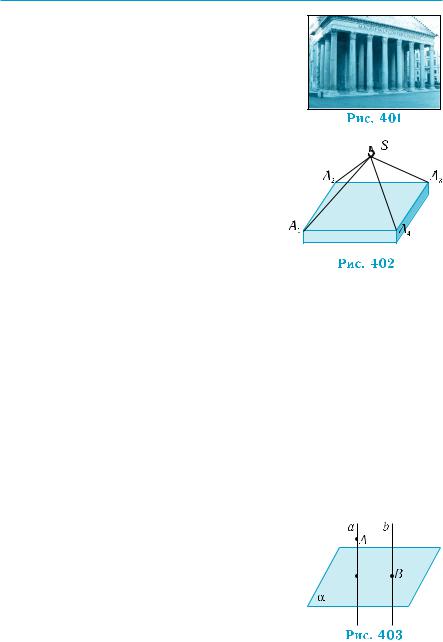
Признак перпендикулярности прямой и плоскости (теорема 3) иллюстрируется рас- положением опорных колонн относительно пола и потолка. Если плоскости потолка и пола параллельны, то колонну достаточ- но поставить перпендикулярно полу, что-
бы она была перпендикулярна и потолку
(рис. 401).
Практическую ценность признака, выраженного в теореме 4, иллюстрирует транспортировка железобетонной пря- моугольной плиты в горизонтальном по- ложении с помощью крана. Для этого ис-
пользуют четыре одинаковых троса, концы которых закреплены в точках А1, А2, А3, А4
плиты и с крюком в точке S (рис. 402). По
скольку плита висит свободно, то трос, на котором закреплен крюк, перпендикулярен поверхности земли и расположен на прямой, проходящей через центр масс плиты (для однородной плиты). Если пренебречь толщиной плиты, то ее центр находится на пересечении диагоналей прямоугольника А1А2А3А4. Поскольку SA1 = SA2 = SA3 = = SA4, то прямая, соединяющая точку S с точкой пересечения диаго- налей, перпендикулярна плоскости плиты (задача 1 §18). Поэтому, согласно теореме 4, плита расположена горизонтально.
Приведенные примеры не исчерпывают всего разнообразия применений рассмотренных признаков при решении практичес- ких задач. Важными являются данные признаки и для последую- щего углубления геометрических знаний.
З а д а ч а 1 . Через данную точку провести прямую, перпенди- |
|
кулярную данной плоскости. |
|
Случай, когда данная точка А лежит |
|
в данной плоскости α, мы рассматривали в |
|
предыдущем параграфе. Пусть теперь точка |
|
А лежит вне плоскости |
α. Через произволь- |
ную точку В плоскости |
α проведем прямую |
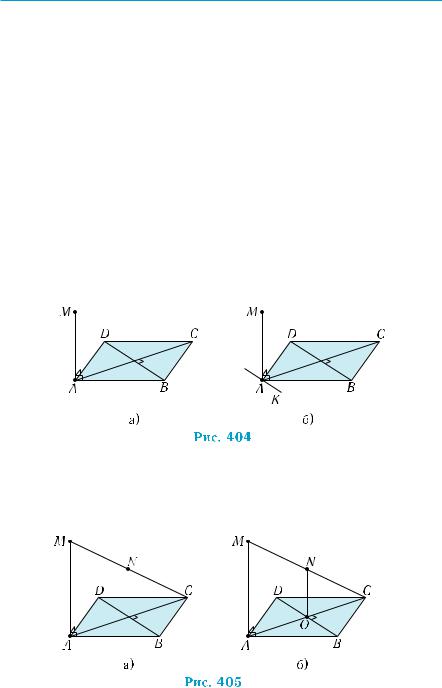
b, перпендикулярную плоскости α (рис. 403). |
|
Потом через точку А проведем прямую, па- |
|
раллельную прямой b |
(как это сделать?). |
Она и будет искомой, поскольку ее перпендикулярность плоскос- |
|
ти α обусловлена теоремой 1. ■ |
|
Связьмеждупараллельностьюиперпендикулярностьюпрямыхиплоскостей 393
П р и м е р 1 . Из вершины A квадрата ABCD проведен отрезок AM, перпендикулярный плоскости ABC. Построить:
1) плоскость, проходящую через точку M перпендикулярно пря- мой АС;
2) прямую, проходящую через середину отрезка MC перпендику- лярно плоскости ABC.
Изобразим условие примера на рис. 404, а.
1) Рассмотрим плоскость МАС. По условию, прямая МА пер- пендикулярна прямой АС. Для построения искомой плоскости достаточно провести через точку А еще одну прямую, перпенди- кулярную прямой АС. Поскольку прямая BD перпендикулярна прямой АС, то искомая прямая должна быть параллельной пря- мой BD.
Построение. Через точку А проведём прямую АK, параллель- ную прямой BD (рис. 404, б). Она перпендикулярна прямой АС. Плоскость МАK перпендикулярна прямой АС, по признаку пер- пендикулярности прямой и плоскости (теорема 1 § 18).
2) Пусть N — середина отрезка МС (рис. 405, а). Искомая прямая параллельнапрямойМА,потеоремеопараллельностипрямых,пер- пендикулярных плоскости (теорема 2). Это — необходимое условие.
394 |
Перпендикулярность прямых и плоскостей |
Оно и достаточно, по теореме о двух параллельных прямых, одна из которых перпендикулярна плоскости (теорема 1).
Построение. Через точку N проведём прямую, параллельную прямой МА (рис. 405, б). Точка ее пересечения О с плоскостью квадрата является центром квадрата, поскольку прямая NО ле- жит в плоскости МАС и проходит через середину отрезка АС (по теореме Фалеса). ■
Рассмотрим доказательство приведенных теорем  о связях между параллельностью и перпендику- лярностью прямых и плоскостей. Указанная связь между двумя парами теорем и между собой в парах
о связях между параллельностью и перпендику- лярностью прямых и плоскостей. Указанная связь между двумя парами теорем и между собой в парах
позволяет надеяться, что доказательство одной из теорем облег- чит доказательство других. Начнем с теоремы 1. Запишем ее в знакосимвольной форме.
Теорема 1. Дано: а1 ||а2, а1 α.
Доказать: а2 α.
Для доказательства теоремы воспользуемся признаком пер-
пендикулярности прямой и плоскости.
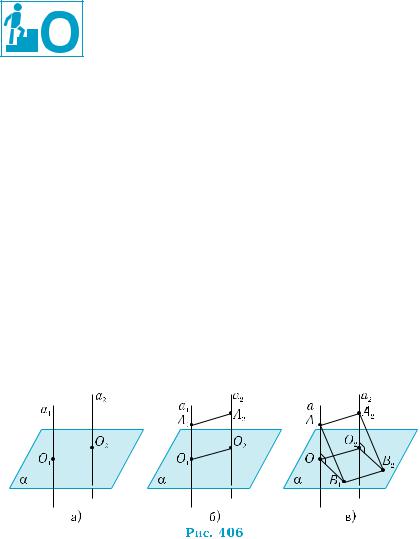
Обозначим через О1 точку пересечения прямой а1 и плоскос- ти α. Согласно теореме о пересечении плоскости параллельными прямыми (теорема 6 § 8), прямая а2, параллельная прямой а1, также пересекает плоскость α в некоторой точке О2 (рис. 406, а).
Возьмем на прямых а1 и а2 точки А1 и А2 по одну сторону от плоскости α так, чтобы отрезки О1А1 и О2А2 были равными. Четы- рехугольник О1А1А2О2 (рис. 406, б) является параллелограммом, так как О1А1 || О2А2, О1А1 = О2А2. Аналогично строим параллело грамм О1В1В2О2 для произвольного направления в плоскости α. Для этого через точки О1 и О2 в плоскости α проведем произволь- ные параллельные прямые, на которых выбираем точки В1 и В2 аналогично выбору точек А1 и А2 (рис. 406, в).
Связьмеждупараллельностьюиперпендикулярностьюпрямыхиплоскостей 395
Из приведенных построений вытекает, что четырехугольник А1В1В2А2 является параллелограммом. Действительно, отрез- ки А1А2 и В1В2 — параллельны и равны, по свойствам транзи- тивности отношений параллельности прямых и равенства длин
(A1A2 || О1О2, O1O2 || B1B2, A1A2 = О1О2, O1O2 = B1B2).
А теперь рассмотрим треугольники А1О1В1 и А2О2В2. Они равны потрёмсторонам:А1О1 = А2О2, О1В1 = О2В2, попостроению,А1В1 =А2В2 как противоположные стороны параллелограмма. Поэтому равны соответствующие углы этих треугольников, в частности, А1О1В1 = = А2О2В2. Но угол А1О1В1 по условию — прямой. Поэтому прямым будет и угол А2О2В2. А это означает, что прямая а2 перпендикулярна каждой прямой плоскости α, проходящей через точку О2. По опреде- лению, она перпендикулярна плоскости α. ■
Теорема 2. Дано: а1 α, а2 α.
Доказать: а1 ||а2.
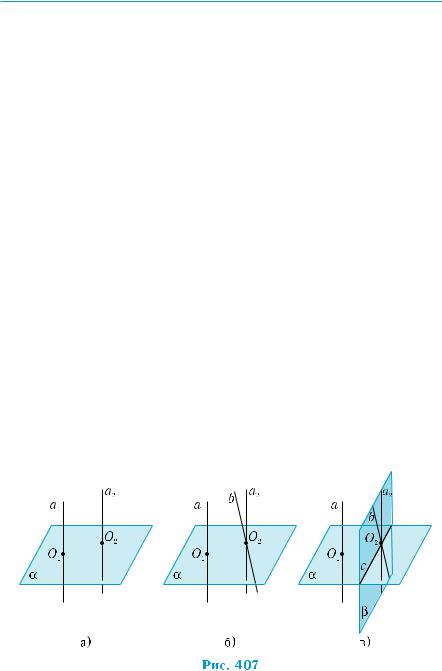
Пусть прямые а1 и а2 перпендикулярны плоскости α, О1, О2 — точки их пересечения с плоскостью α (рис. 407, а). Через точку О2 проведем прямую b, параллельную прямой а1 (рис. 407, б). По те- ореме 1, b α. Если прямая b не совпадает с прямой а2, то через них можно провести плоскость β, пересекающую плоскость α по прямой с (рис. 407, в). Прямые а2 и b перпендикулярны прямой с, по определению перпендикулярности прямой и плоскости. Одна- ко в плоскости через данную точку можно провести лишь одну прямую, перпендикулярную данной прямой. Полученное проти- воречие означает, что прямые а2 и b совпадают, то есть а1 ||а2. ■

396 |
Перпендикулярность прямых и плоскостей |
Доказательство теорем 3 и 4 проводится по такой же схеме, что и доказательство теорем 1 и 2 соответственно. Сделайте это само- стоятельно, пользуясь указанием, приведенным после формули- ровок теорем 3 и 4.
Важностьрассмотренныхтеоремдлястереометриииееприложе- ний, как уже отмечалось, связана с тем, что каждая из них являет- ся признаком: первая и третья — признаками перпендикулярности прямой и плоскости, вторая — признаком параллельности прямых, четвертая — признаком параллельности плоскостей. Этим самым расширяются наши возможности при изучении взаимного располо- жения прямых и плоскостей, проведении построений.
Обобщением результата задачи 1 является следующая тео- рема.
Теорема 5 (о прямой, перпендикулярной данной плоскости).
Через произвольную точку пространства проходит прямая, перпендикулярная данной плоскости, и к тому же только одна.
Первая часть теоремы о существовании такой прямой обоснована в решении задачи
1. Для доказательства единственности та- кой прямой допустим противное, а именно:
через некоторую точку А проходят две раз- личные прямые а1 и а2, перпендикулярные плоскости α (рис. 408). По теореме 2, они па- раллельны, то есть не имеют общих точек.
Это противоречие и доказывает утвержде- ние. ■
Аналогичное обобщение имеет и результат задачи 2 предыду- щего параграфа.
Теорема 6 (о плоскости, перпендикулярной данной прямой).
Черезлюбуюточкупространствапроходитплоскость,перпендикулярная данной прямой, и к тому же только одна.
Существование такой плоскости обос- новано в решении задачи 3 предыдущего параграфа. Осталось доказать единствен- ность плоскости, удовлетворяющей услови- ям теоремы. Как обычно в таких случаях, допустим противное, а именно: через дан-
Связьмеждупараллельностьюиперпендикулярностьюпрямыхиплоскостей 397
ную точку А проходят две различные плоскости α1 и α2, перпенди- кулярные прямой а (рис. 409). По теореме 4, они параллельны. Но эти плоскости имеют общую точку А. Полученное противоречие и доказывает утверждение. ■
П р и м е р 2 . Из вершины А квадрата АBСD проведена прямая, перпендикулярная плоскости квадрата, и на ней взята точка S. Построить:
1) прямую, проходящую через центр О квадрата перпендику- лярно его плоскости;
2) плоскость, проходящую через середину Р отрезка АS перпен- дикулярно ему;
3) плоскость, проходящую через точку А перпендикулярно пря- мой BD;
4) прямую, проходящую через точку А перпендикулярно плос- кости SBD.
1) По условию, прямая AS перпендикулярна плоскости квад- рата. Любая другая прямая, перпендикулярная этой плоскости, будет параллельна прямой AS, по теореме 2, то есть параллель- ность прямой AS является необходимым условием перпендику- лярности искомой прямой плоскости. Она является и достаточ- ным условием, по теореме 1.
Построение. Через точку О прово- дим прямую ОЕ параллельно прямой АS (рис. 410). Прямая ОЕ перпендикулярна плоскости квадрата, по теореме о двух па-
раллельных прямых, одна из которых пер- пендикулярна плоскости.
2)Поусловию,прямаяАSперпендикуляр-
на плоскости АBCD.Любая другая плоскость, 

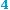 перпендикулярная прямой АS, будет параллельной плоскости ABCD, по теореме 4. Параллельность искомой плоскости плоскости ABCD является, по теореме 3, и достаточным условием.
перпендикулярная прямой АS, будет параллельной плоскости ABCD, по теореме 4. Параллельность искомой плоскости плоскости ABCD является, по теореме 3, и достаточным условием.
Построение. Проведем через точку Р плоскость, параллельную плоскости ABCD.
Для этого через точку Р проведем прямые
РK и РL, параллельные прямым АD и АВ соответственно (рис. 411). Плоскость РKL
параллельна плоскости АBCD, по призна- ку параллельности плоскостей, а потому
является искомой.
398 Перпендикулярность прямых и плоскостей
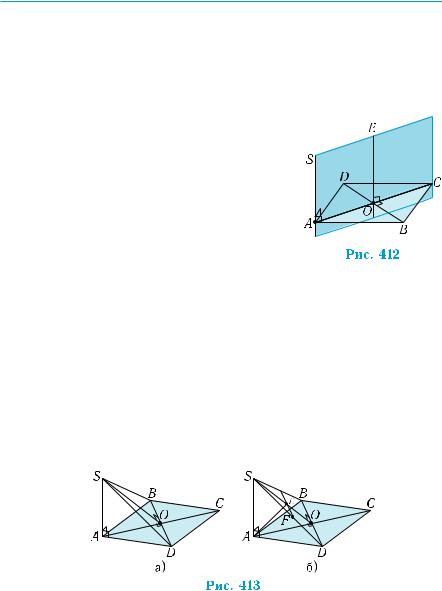
3) Диагонали квадрата перпендикулярны, то есть ВО АО (см. рис. 410). Поэтому прямая АО лежит в искомой плоскости. Если через точку О провести еще одну прямую ОЕ, перпендику- лярную ВО, то прямая ВО будет перпендикулярной плоскости АОЕ, по признаку перпендикулярности прямой и плоскости (тео- рема 1 §18). Эта плоскость содержит точку А.
Построение. Проведем через точку О прямую ОЕ, параллельную прямой АS. Она будет перпендикулярной плоскости АBCD (рис. 412). Прямая ОЕ перпендикулярна
прямой ВО, по определению перпендику- лярности прямой и плоскости. Плоскость АОЕ является искомой.
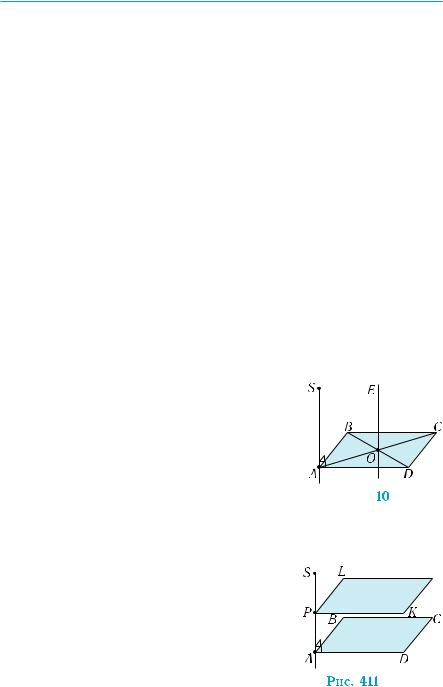
4) Рассмотрим треугольники ABD и SBD
(рис. 413, а). Они равнобедренные, так как
АD = АВ, по условию, а равенство SB = SD вытекает из равенства прямоугольных треугольников ASD и ASB. Их медианы SO и АО являются высотами, а потому прямая BD перпендикулярна плос- кости AOS, по признаку перпендикулярности прямой и плоскости (теорема 1). В прямоугольном треугольнике AOS из вершины пря- мого угла А проведем высоту АЕ (рис. 413, б). Прямая АЕ является искомой. Действительно, проведем в плоскости SBD через точку Е прямую EF параллельно прямой BD. Эта прямая будет перпен- дикулярной плоскости AOS, по теореме 1. А это означает, что она перпендикулярна прямой AE. По признаку перпендикулярности прямой и плоскости (теорема 1 § 18), прямая AE перпендикуляр- на плоскости SBD. ■

Связьмеждупараллельностьюиперпендикулярностьюпрямыхиплоскостей 399
99 Контрольные вопросы
1.Верно ли, что две прямые, перпендикулярные некоторой плоскости, лежат в одной плоскости?
2.Могут ли два боковых ребра пирамиды быть перпендикуляр- ными плоскости основания пирамиды?
3.Можно ли провести прямую, перпендикулярную двум пересе- кающимся плоскостям?
4.Существует ли взаимосвязь между расположением ножек сто- ла относительно его поверхности и пола, на котором он сто- ит?
5.Существует ли сечение куба плоскостью, перпендикулярной ровно двум его рёбрам?
6.Можно ли провести плоскость, перпендикулярную одновре- менно двум скрещивающимся прямым?
7.Почему ледовые сосульки, свисающие с крыши весной, можно считать параллельными между собой (пренебрегая их толщи- ной)?
8.На потолке закреплен крюк. С помощью канатов необходимо подвесить к нему платформу так, чтобы ее плоскость была го- ризонтальной. Как это сделать?
9.Можно ли через данную точку пространства провести три вза- имно перпендикулярные прямые? А четыре?
10.Сколько различных плоскостей определяют четыре прямые, перпендикулярные одной плоскости?
Графические упражнения
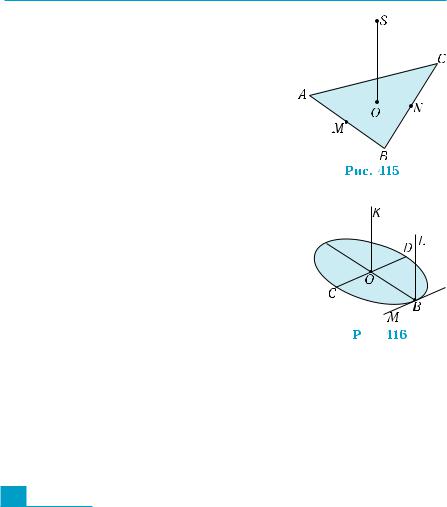
1. На рис. 414 |
изображен прямоугольный |
|
|||||
параллелепипед |
ABCDA1B1C1D1 с квад- |
|
|||||
ратным основанием ABCD, точки M, N, |
|
||||||
P, Q — середины соответственно рёбер |
|
||||||
|
|||||||
ВС, В1С1, АВ, |
D1C1, точки O, O1 — центры |
|
|||||
граней ABCD |
и A1B1C1D1. Установите вза- |
|
|||||
имное расположение указанных прямой |
|
||||||
и плоскости: |
|
2) |
ОМ и ADD1; |
|
|||
1) |
OO1 |
и ABC; |
|
||||
3) |
OC и DBB1; |
4) |
CC1 |
и NQO1; |
|
||
5) |
B1С |
и BAD1; |
6) |
A1C1 |
и MNQ; |
|
|
7) |
РМ |
и BDD1; |
8) |
QN и NPM. |
|
||
400 Перпендикулярность прямых и плоскостей
2. На рис. 415 изображен правильный треугольник ABC, O — его центр, OS —
отрезок, перпендикулярный плоскости треугольника, точки M, N — соответс- твенно середины сторон АВ, ВС. Уста-
новите взаимное расположение: 1) прямой АВ и плоскости SOC;
2) прямой MN и плоскости SOB;
3) прямой АС и плоскости MNS.
3. На рис. 416 изображен круг с центром О, АВ и CD — его взаимно перпенди-
кулярные диаметры, МВ — касательная к окружности, OK, BL — равные отрезки,
перпендикулярные плоскости круга. Ус- 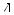 тановите взаимное расположение:
тановите взаимное расположение:
1) прямой BL и плоскости AOC;
2) прямой BM и плоскости LOK;
3) прямой BM и плоскости COK;
4) прямой KL и плоскости DOK;
5)плоскостей DOK и MBL; 

6)прямой BK и плоскости CLD.
4.Постройте рисунок по приведенным данным.
1)Плоскость, проходящая через ребро АВ правильного тетра- эдра SABC, перпендикулярна ребру SC.
2)Через точку М, лежащую на диагонали АС правильной че- тырехугольной пирамиды SABCD, проходит плоскость, пер- пендикулярная АС.
Задачи
407.Из вершины прямого угла С равнобедренного прямоуголь- ного треугольника ABC проведена прямая, перпендикуляр- ная плоскости этого треугольника, и на ней взята точка S. Постройте:
1°) плоскость, проходящую через точку S перпендикулярно прямой AB;
2°) прямую, проходящую через середину отрезка AS перпен- дикулярно плоскости ABC;
3°) плоскость, проходящую через точку A параллельно плос- кости BCS;

Связьмеждупараллельностьюиперпендикулярностьюпрямыхиплоскостей 401
4) прямую, проходящую через точку C перпендикулярно плоскости ABS, если AC = 23 CS.
408. ИзсерединыK гипотенузыBC равнобедренногопрямоуголь- ного треугольника ABC проведена прямая, перпендикуляр- ная плоскости этого треугольника, и на ней взята точка M. Постройте:
1°) плоскость, проходящую через точку M перпендикулярно прямой AC;
2°) прямую, проходящую через середину отрезка AM пер- пендикулярно плоскости ABC;
3°) плоскость, проходящую через точку A параллельно плос- кости BCM;
4) плоскость, проходящую через точку K перпендикулярно прямой AM, если MK = CK.
409. Из центра О правильного треугольника АВС проведена прямая, перпендикулярная плоскости треугольника, и на ней взята точка S. Постройте:
1°) плоскость, проходящую через точку О перпендикулярно прямой ВС;
2°) прямую, проходящую через середину отрезка AS перпен- дикулярно плоскости АВС;
3) плоскость, проходящую через середину отрезка AS пер- пендикулярно прямой OS;
4*) прямую, проходящую через точку А перпендикулярно плоскости BCS.
410. Дан куб ABCDA1B1C1D1. Постройте:
1°) прямую, проходящую через центр грани A1B1C1D1 пер- пендикулярно противоположной грани; 2°) плоскость, проходящую через вершину А перпендику- лярно диагонали BD;
3) прямую, проходящую через центр грани АА1В1В перпен- дикулярно плоскости ВDD1;
4*) плоскость, проходящую через точку D перпендикулярно прямой ВD1.
411. В тетраэдре SАBС все грани — правильные треугольники, точка О — центр АВС, D — середина ребра ВС, точка N при- надлежит ребру SА.

402 |
Перпендикулярность прямых и плоскостей |
1°) Определите взаимное расположение прямой SO и плос- кости АВС.
2°) Определите взаимное расположение прямой ВС и плос- кости ASD.
3) Проведите через точку N прямую, перпендикулярную грани АВС.
4*) Постройте сечение тетраэдра плоскостью, проходящей через точку N перпендикулярно прямой ОS.
412°. Два электрических провода необходимо протянуть от столба высотой 7 м к зданию высотой 4 м. Сколько нужно иметь провода, если расстояние от здания до столба равно 10 м и на провисание провода нужно добавить 3% от его расчетной длины?
413. Сторожевая башня для охраны участка прямоугольной фор- мы установлена в одной из вершин прямоугольника. Рассто- яния от наблюдателя, стоящего на башне, до остальных вер- шин прямоугольника равны а, b, с, причем а > b > с. Чему равняется высота башни?
414. Три параллельные прямые а, b, с не лежат в одной плос- кости. Через точку М, лежащую на прямой а, проведены перпендикуляры к прямым b и с, пересекающие их, соот- ветственно, в точках Р и Q. Докажите, что прямая РQ пер- пендикулярна прямым b и с.
415. Через точку О, находящейся на высоте СD треугольника АBС, проведен перпендикуляр ОМ к его плоскости. Дока- жите, что плоскость, проходящая через прямые СD и ОМ, перпендикулярна прямой АB.
416*. Даны плоскость α и прямая а, пересекающая плоскость в точке М и не перпендикулярная α. Докажите, что в плос- кости α через точку М проходит прямая, перпендикулярная прямой а, и к тому же лишь одна.
417. На прямой, перпендикулярной плоскости α, взяты две точ- ки А и В, не лежащие в плоскости α, а в плоскости α взяты две точки X и Y. Известно, что ХА > ХB. Сравните отрезки
YА и YВ.
Связьмеждупараллельностьюиперпендикулярностьюпрямыхиплоскостей 403
Упражнения для повторения
418.Докажите, что все прямые плоскости, перпендикулярные данной прямой плоскости, образуют эту плоскость.
419.Как разделить отрезок пополам, пользуясь лишь шаблоном: а) прямого угла; б) острого угла?
420.Стороны параллелограмма равны 2 м и 16 дм; расстояние между большими сторонами — 8 дм. Определите расстояние между меньшими сторонами.
Итог
Основные утверждения
|
|
|
|
|
|
||
Теорема о двух |
Если одна из двух па- |
|
|
|
|
||
|
|
|
|
||||
параллельных |
раллельных |
прямых |
|
|
|
|
|
прямых, одна из |
перпендикулярна |
|
|
|
|
||
которых перпенди- |
плоскости, то и вторая |
|
|
|
|
||
кулярна плоскости |
прямая |
перпендику- |
a || b, a α b α |
||||
|
лярна этой плоскости. |
|
|
|
|
||
Теорема о парал- |
Если две прямые пер- |
|
|
|
|
||
|
|
|
|
||||
лельности прямых, |
пендикулярны одной |
|
|
|
|
||
перпендикулярных |
и той же плоскости, то |
|
|
|
|
||
плоскости |
они параллельны. |
|
|
|
|
||
|
|
|
|
a α, b α a || b |
|||
|
|
|
|
|
|
||
Теорема о парал- |
Если одна из двух па- |
|
|
|
|
||
|
|
|
|
||||
лельных плос- |
раллельных |
плоскос- |
|
|
|
|
|
костях, одна из |
тей перпендикулярна |
|
|
|
|
||
которых перпенди- |
прямой, то и вторая |
|
|
|
|
||
кулярна прямой |
плоскость |
перпенди- |
|
|
|
|
|
|
|
|
|
||||
|
кулярна этой прямой. |
α || β, α l β l |
|||||
|
|
|
|
||||
|
|
|
|
|
|
|
|
Теорема о двух |
Если две |
плоскости |
|
|
|
|
|
|
|
|
|
||||
плоскостях, пер- |
перпендикулярны од- |
|
|
|
|
||
пендикулярных |
ной прямой, то они |
|
|
|
|
||
прямой |
параллельны. |
|
|
|
|
||
|
|
|
|
α l,β l α || β |
|||
|
|
|
|
|
|
|
|
