
- •Обращение к читателю
- •Введение
- •РАЗДЕЛ 1. Функции, их свойства и графики
- •§1. Числовые множества
- •§2. Вычисления и расчёты
- •§3. Функциональные зависимости
- •§4. Основные свойства функций
- •§5. Корни n-ой степени
- •§6. Степенные функции с рациональными показателями
- •§7. Основные понятия и аксиомы стереометрии
- •§8. Взаимное расположение двух прямых в пространстве
- •§9. Параллельное проектирование
- •§10. Изображение фигур в стереометрии
- •§11. Параллельность прямых и плоскостей
- •§12. Параллельность плоскостей
- •§13. Тригонометрические функции числового аргумента
- •§14. Основные соотношения между тригонометрическими функциями
- •§15. Свойства и графики тригонометрических функций
- •§16. Тригонометрические формулы сложения и следствия из них
- •§17. Простейшие тригонометрические уравнения и неравенства
- •§18. Перпендикулярность прямой и плоскости
- •§19. Связь между параллельностью и перпендикулярностью прямых и плоскостей
- •§20. Перпендикулярность плоскостей
- •§21. Ортогональное проектирование
- •§23. Измерение расстояний в пространстве
- •§24. Измерение углов в пространстве
- •Ответы и указания к задачам
- •Предметный указатель
- •Содержание

§24. измерение углов в пространстве
Ðассматриваются понятия угла между прямыми и плоскостями, а также между плоскостями.
 Взаимное расположение прямых, прямых и плос-
Взаимное расположение прямых, прямых и плос-

 костей, а также плоскостей характеризуют в стереометрии различными способами. Один из них базируется на количестве общих точек этих фигур. Он приводит к
костей, а также плоскостей характеризуют в стереометрии различными способами. Один из них базируется на количестве общих точек этих фигур. Он приводит к
важным отношениям между прямыми и плоскостями — отношениям параллельности. Уточнение взаимного расположения указанных фигур осуществляется с помощью отношений перпендикулярности. Они отражают определенную симметрию взаимного расположения фигур. Рассмотрение расстояний между фигурами дает возможность характеризовать их взаимное расположение с помощью чисел. Последующее уточнение взаимного расположения прямых и плоскостей осуществляется с помощью измерения углов между этими фигурами. Необходимость таких измерений вызвана потребностями как геометрии, так и практики. Измерения углов необходимы в геометрии, геодезии, мореходном деле, космонавтике и т. п. Их применяют и в повседневной жизни
(рис. 502 – 504).
Две пересекающиеся прямые пространства определяют некоторую плоскость. Для числовой характеристики их взаимного расположения используют, как и в планиметрии, понятие угла меж-
Измерение углов в пространстве |
453 |
ду ними. Этой величиной мы уже неоднократно пользовались. Напомним ее определение.
Углом между пересекающимися прямыми называ ется величина наименьшего из углов, образованных этими прямыми.
По определению, угол между прямыми является величиной, принимающей значения в пределах от 0° до 90°. Угол между па- раллельными прямыми считают равным 0°, а между перпендику- лярными — 90°.
Введем аналогичную характеристику для пересекающихся прямой и плоскости. Практическую необходимость в измерении угла между прямой и плоскостью можно проиллюстрировать на примерах. Такими измерениями издавна пользовались морепла- ватели при определении положения корабля (рис. 505, а). Они необходимы геодезистам, проводящим работы на местности, стро- ителям при установлении конструкций и т. п. (рис. 505, б, в).
Для измерения угла между прямой а и плоскостью α следует об- ратиться к измерению углов между данной прямой и прямыми, ле- жащими в плоскости α и пересекающими прямую а. Однако таких прямых в плоскости α бесконечное множество, и указанные углы различныповеличине.Преимуществоимеетуголмеждупрямойаи ее ортогональной проекцией, если прямая а не перпендикулярна плоскости α. Этот угол опре-  деляетсяоднозначно,посколькуортогональная проекциядлякаждойпрямойопределенаодно-
деляетсяоднозначно,посколькуортогональная проекциядлякаждойпрямойопределенаодно-
значно (рис. 506). В практических приложени- ях соответствующую величину легко измерять, и она удобна для характеристики наклона пря-
мой к плоскости.
454 |
Перпендикулярность прямых и плоскостей |
Углом между прямой и неперпендикулярной ей плос костью называется угол между прямой и ее ортого нальной проекцией на эту плоскость.
Напомним, что угол между пересекающимися прямыми при- нимает значения в пределах от 0 к 90°. Поэтому и угол между прямой и плоскостью является величиной, принимающей значе- ния в этих пределах.
Если наклон прямой к плоскости непрерывно уменьшать, то предельным положением подвижной прямой будет прямая, ле- жащая в плоскости (рис. 507).
Угол между прямой и плоскостью, в которой она ле жит, считают равным 0°.
Если же наклон прямой к плоскости непрерывно увеличивать, то предельным положением подвижной прямой является прямая, перпендикулярная плоскости (рис. 507).
Угол между прямой и перпендикулярной ей плоскос тью считают равным 90°.
Обратим внимание еще на одну особенность угла между пря- мой, пересекающей плоскость, и ее ортогональной проекцией на эту плоскость. Этот угол является наименьшим среди всех других углов между данной прямой и прямыми, пересекающими ее и ле- жащими в данной плоскости (рис. 508).
Действительно, пусть прямая а пересекает плоскость α, ВР — перпендикуляр к этой плоскости, а1 — ее ортогональная проекция на плоскость α, с — произвольная прямая, лежащая в плоскости α и проходящая через точку А пересечения прямой а и плоскости α (рис. 508). Угол между прямыми а и а1 равен величине угла ВАР прямоугольного треугольника АВР, а угол между прямыми а и с — величине угла ВАС прямоугольного треугольника АВС.
Измерение углов в пространстве |
455 |
Прямоугольные треугольники АВС и АВР имеют общую гипоте- нузу, катет одного треугольника является наклонной, а друго- го — перпендикуляром к плоскости. Сравнение углов ВАС и ВАР дает возможность прийти к указанному выводу.
!Под углом между отрезком и плоскостью, между отрезком и плоской фигурой (например, между диагональю куба и его гранью) понимают угол между соответствующими прямой и плоскостью.
При решении задач прямые, пересекающие плоскость, задают- ся с помощью наклонных к плоскости.
Пусть АВ — наклонная к плоскости α, АР — ее проекция (рис. 509). Угол ВАР является од- ним из углов, образованных прямыми АВ и АР.
Поскольку треугольник АВР — прямоуголь- ный, то угол ВАР — острый, то есть его угло- вая мера равна углу между прямыми АВ и АР.
Следовательно, мы показали, что угол между 

 наклонной и ее проекцией равен углу между прямой, заданной наклонной, и плоскостью. Это дает возможность
наклонной и ее проекцией равен углу между прямой, заданной наклонной, и плоскостью. Это дает возможность
отождествлять названные величины при решении задач.
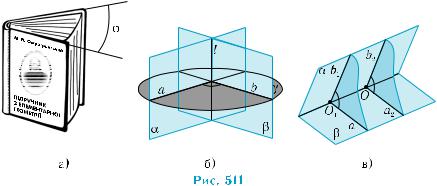
Мы рассмотрели понятие угла между плоскостью и пересекаю- щей её прямой. Таким образом, мы ввели числовую характеристи- ку их взаимного расположения. Дальше рассмотрим особенности взаимного расположения двух пересекающихся плоскостей. Это задание связано с практической деятельностью человека и при- годится при оценивании наклона крыши к поверхности земли (рис. 510, а), учета профиля местности при строительстве дороги (рис. 510, б), при изготовлении резцов с различными свойствами резания (рис. 510, в) и т. п. Следовательно, необходимо уметь ха- рактеризовать взаимное расположение непараллельных плоскос- тей с помощью числа после выбора единицы измерения.
456 |
Перпендикулярность прямых и плоскостей |
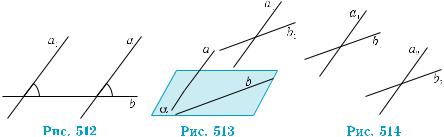
Как и в случае определения угла между прямой и плоскостью, попробуем найти плоский угол, характеризующий взаимное распо- ложение двух плоскостей. Глядя на обложки полураскрытой книги (рис. 511, а), нетрудно увидеть, что мерой взаимного расположения обложек (мерой «развёрнутости» книги) может быть величина угла α, образованного краями обложек. Если рассматривать плоскости, в которых расположены эти обложки, то угол α получают как резуль- тат пересечения данных двух плоскостей третьей плоскостью, пер- пендикулярной линии пересечения первых двух плоскостей.
Углом между пересекающимися плоскостями назы вается угол между прямыми, образующимися при пересечении данных плоскостей плоскостью, пер пендикулярной линии их пересечения.
Пусть α и β — две плоскости, пересекающиеся по прямой l (рис.511,б).Черезпроизвольнуюточкупрямойl проведемплоскость γ, перпендикулярную прямой l. Эта плоскость пересекает плоскос- ти α и β по прямым а и b. Угол между этими прямыми и является углом между данными плоскостями. Остается лишь убедиться, что угол между плоскостями не зависит от места проведения секущей плоскости. Для этого рассмотрим два различных пересечения, про- ходящие через точки О1 и О2 (рис. 511, в). Обозначим через а1 и а2 линиипересечениясекущихплоскостейсплоскостью α.Этипрямые параллельны, поскольку в плоскости α они перпендикулярны пря- мой l. Из тех же соображений параллельными являются и прямые b1 и b2 — линии пересечения секущих плоскостей с плоскостью β. Таким образом, речь идет о равенстве углов между прямыми а1, b1 и параллельными данным прямыми а2, b2. В планиметрии этот факт хорошо известен. Он имеет место и в стереометрии.
Измерение углов в пространстве |
457 |
Теорема 1 (о равенстве углов между соответственно парал- лельными прямыми).
Если две пересекающиеся прямые соответственно параллельны двум пересекающимся прямым, то углы между этими парами прямых равны.
Доказательство этой теоремы будет приведено далее. Напомним, что угол между прямыми принимает значения в
пределах от 0° до 90°. В этих пределах принимает значения и угол между плоскостями. В частности, угол между совпадающими
плоскостями естественно считать равным 0°. Если же
угол между плоскостями равен 90°, то плоскости перпен дикулярны, по второму признаку перпендикулярности плоскос- тей (теорема 3 §20). Обратно, угол между перпендикулярными плоскостями равен 90°. Следовательно, можно прийти к такому выводу.
Теорема 2 (признак перпендикулярности плоскостей).
Две плоскости перпендикулярны тогда и только тогда, когда угол между ними равен 90°.
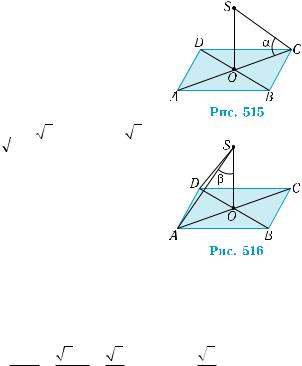
Рассмотрение измерения углов в пространстве завершим вве- дением понятия угла между скрещивающимися прямыми. Угол между пересекающимися прямыми характеризует наклон од- ной прямой к другой. При замене прямой на параллельную ей прямую этот наклон не изменяется (рис. 512). Это свойство углов между пересекающимися прямыми и лежит в основе определения угла между скрещивающимися прямыми.
Углом между скрещивающимися прямыми называ ется угол между параллельными им пересекающи мися прямыми.
Угол между скрещивающимися прямыми а и b на рис. 513 из- меряется углом между пересекающимися прямыми а1 и b1, соот-
458 |
Перпендикулярность прямых и плоскостей |
ветственно параллельными прямым а и b. Остаётся только обос- новать, что эта величина не зависит от выбора прямых а1 и b1, параллельных соответственно а и b. То есть, если взять другую пару пересекающихся прямых а2 и b2, параллельных а и b, то угол между ними равен углу между прямыми а1 и b1 (рис. 514). Истин- ность этого утверждения составляет содержание теоремы 1, при- веденной выше.
Пример 1. |
Пусть OS — перпендикуляр к плоскости квадрата |
ABCD с центром в точке О; OS = AB = 2. |
|
1) Найти угол между прямой CS и плоскостью ABD. |
|
2) Найти угол между прямой AS и плоскостью DBS. |
|
3) Найти угол между прямой, проходящей через точку S и середи- |
|
ну стороны АВ, и плоскостью DBS. |
|
1) Построим рис. 515, который соответс- |
|
твует условию примера. Прямая ОС являет- |
|
ся ортогональной проекцией прямой CS на |
|
плоскость ABD. По определению угла между |
|
прямой и плоскостью, искомый угол α равен |
|
величине угла OCS. Из прямоугольного тре- |
|
угольника SOC имеем: |
|
tgα = |
SO |
= |
2SO |
= |
2 2 |
= 2, α = arctg 2. |
|
OC |
AC |
2 2 |
|||||
|
|
|
|
2) Найдем ортогональную проекцию пря- мой AS на плоскость DBS (рис. 516). Нетруд- но убедиться в том, что это прямая SO. Дейс- твительно, AO BD, по свойству диагоналей квадрата, AO SO, поскольку SO ABC. Поэтому, по признаку перпендикулярности прямой и плоскости, AO DBS и точка O яв-
ляется основанием перпендикуляра AO.
По определению угла между прямой и плоскостью, искомый |
||||
угол β равен величине угла ASO. Из прямоугольного треугольни- |
||||
ка ASO имеем: |
|
|
|
|
tgβ = AO = |
AC = |
2 2 = |
2 , |
β = arctg 2 . |
SO |
2SO |
2 2 |
2 |
2 |
Этот ответ можно было получить, пользуясь решением зада-
ния 1).
Треугольники AOS и COS равны по трём сторонам. Поэтому

Измерение углов в пространстве |
|
|
|
|
1 = |
1 = |
2 . |
459 |
|||
β = π |
− α , где tgα = 2. |
Отсюда tgβ = ctgα = |
|
|
|||||||
2 |
|
|
|
|
|
|
tgα |
2 |
2 |
|
|
3) Пусть K — середина стороны АВ. По |
|
|
|
|
|
|
|||||
строим ортогональную проекцию прямой KS |
|
|
|
|
|
|
|||||
на плоскость DBS. Для этого проведем из |
|
|
|
|
|
|
|||||
точки K |
прямую KP, параллельную прямой |
|
|
|
|
|
|
||||
AO (рис. 517), где точка P |
— середина отрез- |
|
|
|
|
|
|
||||
ка OB — является точкой ее пересечения с |
|
|
|
|
|
|
|||||
плоскостью |
DBS. Поскольку AO является |
|
|
|
|
|
|
||||
перпендикуляром к плоскости DBS (см. ре- |
|
|
|
|
|
|
|||||
шение задания 2)), то KP |
— перпендикуляр |
|
|
|
|
|
|
||||
к ней, по теореме о двух параллельных прямых, одна из которых |
|||||||||||
перпендикулярна плоскости (теорема 1 §19). Ортогональной про- |
|||||||||||
екцией прямой KS на плоскость DBS является прямая SP. Иско- |
|||||||||||
мый угол γ равен величине угла KSP. Из прямоугольного тре |
|||||||||||
угольника KPS имеем: tg γ = KP . Отрезок KP является средней |
|||||||||||
|
|
|
|
SP |
1 AO = |
1 AC = 2 |
2 = |
2 . |
|||
линиейтреугольникаAOB,поэтому KP = |
|||||||||||
|
|
|
|
|
2 |
|
|
4 |
4 |
|
2 |
Из прямоугольного треугольника SOP имеем: SP = |
SO2 +OP2 = |
||||||||||
1 |
|
3 |
2 |
3 |
1 |
|
|
1 |
|
||
= 4 + 2 |
= |
|
2 . Таким образом, tgγ = 2 : |
2 = |
|
3 |
, γ = arctg |
3 . ■ |
|
||
Ответ: 1) arctg 2; 2) arctg 22 ; 3) arctg 13 .
Пример 2. Антенну закрепляют с помощью четырех растяжек одинаковой длины, изготовленных из троса. Известно, что для надежного крепления антенны растяжки должны быть натянуты под углом, не превышающим 60° к поверхности земли. Хватит ли 80 м троса для крепления, если точка креп- ления располагается на высоте 15 м над по- 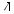 верхностью земли и на закрепление одной растяжки идет до 1 м троса?
верхностью земли и на закрепление одной растяжки идет до 1 м троса?
Установленная антенна схематически изображена на рис. 518. Здесь ОА — схе- матическое изображение антенны, а А — место крепления растяжек на антенне, В, С, В1, С1 — точки крепления растяжек на

460 |
Перпендикулярность прямых и плоскостей |
земле. По условию, АО = 15 м, АВ = AC = АВ1 = AC1. Углы ABO, ACO, АВ1О, АС1О равны между собой и не превышают 60°. Обоз- начим их угловую меру через α. Наиболее экономное крепление соответствует случаю, когда α = 60°. Из прямоугольного треуголь ника АОВ имеем:
АВ = sin60AO ° = 2 135 ≈17,4 (м).
Таким образом, на изготовление одной растяжки нужно не менее чем 18,6 м троса, а на изготовление четырех — 74,4 м. Следовательно, имеющего троса хватит для установления ан- тенны. ■
Ответ. Хватит.
Значимость отношения параллельности прямых 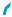
 связана с тем, что при замене прямой на парал-
связана с тем, что при замене прямой на парал-  лельную ей прямую сохраняются многие геометри- ческие отношения и величины. Например, сохра- няются величины углов с одинаково направленными сторонами.
лельную ей прямую сохраняются многие геометри- ческие отношения и величины. Например, сохра- няются величины углов с одинаково направленными сторонами.
Пусть даны два угла АОВ и А1О1В1 и известно, что луч ОА на- правлен так же, как и луч О1А1, а луч ОВ — как луч О1В1. Такие углы называются углами с одинаково направленными сто ронами. В этом определении понятие одинаковой направленнос- ти в пространстве аналогично понятию одинаковой направлен- ности в плоскости.
Два луча ОА и О1А1 в пространстве, не лежащие на одной прямой, одинаково направлены, если они па раллельны и принадлежат одной полуплоскости, ограниченной прямой ОО1. Два луча, лежащие на од ной прямой, одинаково направлены, если один из них полностью принадлежит второму.
Как и в планиметрии, справедливо следующее утверждение.
Теорема 3 (об углах с одинаково направленными сторонами).
Углы с одинаково направленными сторонами равны между собой.
Проведем через стороны угла АОВ плоскость α. Если угол А1О1В1 имеет с углом АОВ одинаково направленные стороны, то возможны лишь два случая: прямые О1А1 и О1В1 не имеют общих

Измерение углов в пространстве |
461 |
точек с плоскостью α или же они обе лежат в плоскости α. Дейс- твительно, параллельные прямые О1А1 и О1В1 не могут пересе- кать плоскость α, поскольку они параллельны прямым ОА и ОВ.
Рассмотрим первый случай (рис. 519). Пусть ОА = О1А1, ОВ = О1В1. Тогда четырехугольник ОАА1О1 — параллелограмм (он лежит в плоскости, определяемой параллельными прямыми ОА и О1А1, и имеет равные противоположные стороны). Аналогич- но, четырехугольник О1В1ВО также является параллелограммом. Поскольку АА1 || ОО1, ОО1 || ВВ1 и АА1 = ВВ1, то четырехугольник АА1В1В — параллелограмм и АВ = А1В1. Треугольники АОВ и А1О1В1 равны по трем сторонам, а потому равны между собой углы
АОВ и А1О1В1.
Во втором случае имеем одну плоскость α. Если стороны углов не лежат на одной прямой, то доказательство аналогично приве- денному выше (рис. 520). Если же стороны углов (например, ОА и О1А1) лежат на одной прямой (рис. 521), то нужно воспользоваться свойством углов, образованных при пересечении двух параллель- ных прямых третьей. ■
Возвратимся к теореме 1 о равенстве углов между соответствен- но параллельными прямыми.
Пусть даны две пары пересекающихся прямых а1, а2 и b1, b2 и а1|| b1, а2||b2. Прямые а1, а2 образуют четыре, попарно равных меж- ду собой, угла, которым соответствуют четыре угла с одинаково направленными сторонами, образованными прямыми b1 и b2.
Из теоремы 4 непосредственно вытекает, что угол между пря- мыми а1 и а2 равен углу между прямыми b1 и b2. Таким образом, теорема 1, которой мы пользовались при введении понятий угла между плоскостями и скрещивающимися прямыми, доказана. ■
Отметим, что в практических задачах более распространенной является не конструкция из двух пересекающихся плоскостей, а
462 |
Перпендикулярность прямых и плоскостей |
конструкция из двух полуплоскостей, имеющих общую границу (скаты крыши, обложки книги, стенки желоба и т. п.).
Фигура, образованная двумя полуплоскостями, имею щими общую границу, называется двугранным углом. Общая прямая полуплоскостей называется ребром, а сами полуплоскости — гранями двугранного угла.
Двугранный угол с ребром АВ и точками М, N, принадлежа- щими различным граням (рис. 522), будем обозначать МABN.
Угловая мера двугранного угла может отличаться от угла между плоскостями, определяемыми гранями двугранного угла. Действительно, книга на рис. 523 «развернута больше», чем на рис. 511, а), но угол между плоскостями-обложками на рис. 523 — в данном случае меньше, чем на рис. 511, а).
Плоскость γ, перпендикулярная ребру двугранного угла, пере- секает его грани по двум полупрямым а и b (рис. 524), выходящим из общей точки О. Построенный таким образом угол называется
линейным углом двугранного угла. Собственно, он и опреде-
ляет угловую меру двугранного угла. Понятно, что линейный угол двугранного угла как геометрическая фигура определяется неод- нозначно, но все линейные углы данного двугранного угла равны между собой. Обоснование этого факта аналогично рассуждениям о произвольности выбора секущей плоскости при измерении угла между плоскостями.
Вотличиеотугламеждуплоскостями,принимающегозначения в пределах от 0° до 90°, угловая мера двугранного угла принимает значения от 0° до 180°. Это отличие связано с тем, что в первом случае измеряется угол между прямыми, а во втором — плоский угол, который может быть и острым, и тупым. Однако, существует простая связь между этими величинами: они или равны, или же в

Измерение углов в пространстве |
463 |
сумме равны 180°. Так, на рис. 525 изображен двугранный угол и прямые а и b, проходящие через стороны его линейного угла. Двугран- ный угол равен β. Но угол между прямыми а и b равен α, если β > 90°. Понятно, что β + α
= 180°.
Для построения линейного угла достаточ- но взять точку на ребре двугранного угла и
из этой точки в каждой грани провести лучи, перпендикулярные ребру.
Иногда при определении двугранного угла в него включают и часть пространства, содержащуюся между его гранями.
Понятие угла между плоскостями позволяет установить связь между площадью плоской фигуры и площадью ее ортогональной проекции.
Задача 1. Доказать, что площадь SАВС треугольника АВС и площадь SA1B1C1 его ортогональной проекции А1B1C1 на плоскость
α связаны соотношением:
SA1B1C1 = SABC cosϕ,
где ϕ — угол между плоскостями АВС и α.
Можно считать, что линия пересечения плоскостей АВС и α проходит через одну из сторон треугольника АВС (например, АВ, рис. 526, а) или через одну из вершин (например, А, рис. 526, б). Этого можно достичь параллельным переносом плоскости α, в ре- зультате которого проекция не изменяется.
В первом случае треугольник АВС и его проекция А1В1С1 име- ют общее основание АВ, а угол ϕ равен углу CDC1 между высота- ми этих треугольников. Поскольку DC1 = DCcos ϕ, то

464 Перпендикулярность прямых и плоскостей
= 12 AB DC1 = 12 AB DC cosϕ = SABC cosϕ.
Во втором случае рассмотрим треугольник ACK, где K — точка пересечения прямой BC с линией пересечения плоскостей ABC и α (BC не параллельна α, иначе, перенеся параллельно плоскость α, мы пришли бы к первому случаю). Треугольник ABC можно по- лучить, «отрезав» от треугольника ACK треугольник ABK, основа- ние которых AK лежит на линии пересечения плоскостей ABC и α. Аналогичное соотношение имеем для проекций треугольников. Поэтому
SA1B1C1 = SAC1 K − SAB1 K = SACK cosϕ − SABK cosϕ = SABC cosϕ.
Каждый многоугольник можно разбить на треугольники. При этом площадь многоугольника равна сумме площадей треуголь- ников разбиения. Кроме того, разбиению многоугольника на тре- угольники соответствует разбиение его ортогональной проекции на треугольники, являющиеся ортогональными проекциями тре- угольников, на которые разбит многоугольник. Из приведенных соображений и задачи 1 вытекает следующая теорема.
Теорема 4 (о площади ортогональной проекции многоуголь- ника).
Площадь ортогональной проекции многоугольника равна произведению площади этого многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции.
На самом деле теорема справедлива для произвольной плос- кой фигуры, для которой определена площадь, ведь для нее пло- щадь можно определить с любой точностью с помощью площадей вписанных многоугольников.
Пример 3. Равнобокую трапецию ABCD с большим основани- ем AD и высотой 8 см перегнули по прямой, проходящей через се- редины M и N сторон AB и CD, так, что вершина B расположилась от плоскости AMN на расстоянии 2 см.
1)Найти угол между плоскостями AMD и MBC.
2)Построить линейный угол двугранного угла AMNC и найти его угловую меру, если ортогональная проекция точки C на плоскость четырехугольника AMND лежит за его пределами.
3)Найти расстояние от точки B до прямой AD.

Измерение углов в пространстве |
465 |
4)Найти расстояние от прямой АN до плоскости АВD.
5)Построить линию пересечения плоскостей АМВ и DNC.
Языком геометрических преобразований условие примера можно интерпретировать как поворот части трапеции МВСN во круг средней линии МN данной трапеции (рис. 527, а), при ко- тором каждая точка, в частности точки В, С и др., вращаются в
плоскости, проходящей через эту точку и перпендикулярной МN. 1) Построим рис. 527, б), в), соответствующие условию. Расстоя- ние от точки B до плоскости AMN определяется длиной перпенди- куляра BP, основание которого P лежит на прямой BE (рис. 527, а) или на прямой KE (рис. 527, б), где K — точка пересечения высоты BE трапеции ABCD со средней линией MN. При этом точка P мо- жет лежать на луче KE (рис. 527, б) или же на дополнительном
луче до всей прямой KE (рис. 527, в).
В обоих отмеченных случаях угол между плоскостями AMD и MBC равен углу BKP одноименного прямоугольного треугольни- ка, ведь плоскость BKE перпендикулярна MN и угол BKP — ост- рый угол прямоугольного треугольника. Поскольку BK = 4 см,
BP = 2 см, то sin BKP = 2 = 1 , BKP = 30°.
42
2)Этому условию соответствует рис. 527, в), ведь KP < 4 см и если бы точка P принадлежала лучу KE, то она бы находилась на отрезке KE, т.е. внутри четырехугольника. А расположение про- екций точек B и C относительно четырехугольника AMND одина- ково. Поэтому линейным углом двугранного угла AMNC может быть угол BKE, а его мера равна 180° – 30° = 150°.
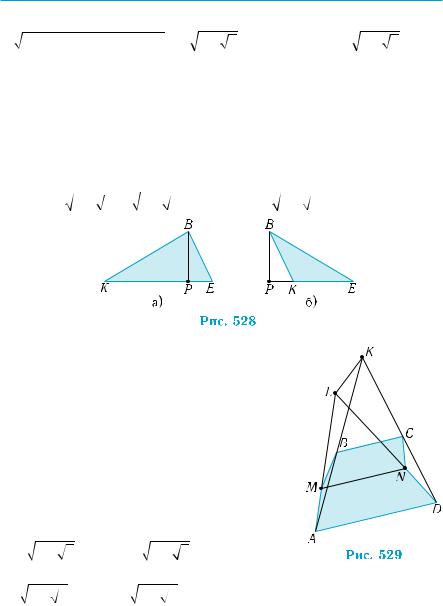
3)Поскольку BE AD, то расстояние от точки B до прямой AD определяется длиной стороны BE треугольника BKE. И опять имеем два случая, когда BKE = 30° и BKE = 150° (рис. 528, а, б),
466 Перпендикулярность прямых и плоскостей
а KB = KE = 4 см в обоих случаях. Тогда, по теореме косинусов, BE =
= 42 + 42 − 2 4 4 cos30° = 4 2 − 3 (см) или BE = 4 2 + 3 (см).
4)РасстояниеотпрямойMN доплоскостиABD определяетсядли-
ной перпендикуляра из точки K к плоскости ABD. А поскольку плос- кости ABD и KBE перпендикулярны (почему?), то искомый перпен- дикуляр является высотой h треугольника KBE, проведенной из вершины K. И опять имеем два случая (рис. 528, а, б). В обоих из них
высоту к стороне ВЕ можно найти как отношение удвоенной площа- |
||||||
ди 2S = KE BP = 4 |
2 = 8 (см2) треугольника KВЕ к стороне ВЕ. То |
|||||
8 |
|
2 |
|
2 |
|
|
есть h = |
|
= |
|
(см) или h = |
|
(см). |
4 2 + 3 |
2 + 3 |
2 − 3 |
||||
5) Возвратимся к рис. 527, б), в). Прямую,
по которой пересекаются плоскости АВМ и DСN, можно задать, определив две ее точ- ки. Одну из них, точку K, можно получить как пересечение прямых АВ и DС этих плос-
костей. Причем эти прямые обязательно пе-
ресекаются, поскольку они проходят через
боковые стороны АВ и DС. Вторая точка L
находится как точка пересечения прямых |
||||||
АМ |
и DN, проходящих через боковые сторо- |
|||||
ны трапеции АМND (рис. 529). |
||||||
Ответы: 1) 30°; 2) 150°; |
|
|||||
3) 4 |
2 − |
3 см или 4 2 + |
3 см; |
|||
4) |
|
2 |
|
см или |
2 |
см. |
|
2 + |
3 |
2 − 3 |
|||

Измерение углов в пространстве |
467 |
99 Контрольные вопросы
1. На рис. 530 изображены две наклонные АВ и АС и их проекции ВР и РС на плос- кость α. Какая из наклонных образует меньший угол с плоскостью α, если:
1) АС = 4, АВ = 6;
2)АС = 5, АВ = 3?
2.Из центра О квадрата ABCD проведен перпендикуляр OS к плоскости квадра- та, точки N, M — середины сторон BC и AD (рис. 531). Величина какого угла является углом между:
1)прямой SN и плоскостью ADC;
2)прямой OS и плоскостью BCS;
3)плоскостями ASD и ABC;
4)плоскостями ASD и ВSC;
5) прямыми AS и BC? 


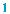
3.Может ли угол между прямой и плоскостью равняться 130°; –70°; 20°?
4.Будут ли равными в тетраэдре боковые рёбра, если они обра- зуют равные углы с плоскостью основания?
5.Верно ли, что угол между прямой, перпендикулярной плос- кости, и произвольной прямой этой плоскости равняется 90°?
6.Как определить, пользуясь лишь рулеткой, угол наклона столба к земле?
7.Что нужно измерить, чтобы определить: а) высоту башни, к основанию которой наблюдатель может подойти; б) расстоя- ние до дома, высота которого известна, если наблюдатель не может к нему подойти?
Графические упражнения
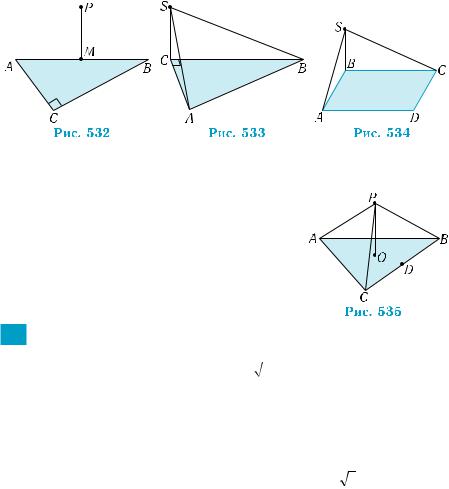
1.Из середины М гипотенузы прямоугольного треугольника АВС проведен перпендикуляр МР к плоскости треугольника (рис. 532). Сравните углы наклона прямых РА, РВ, РС к плос- кости АВС.
2.Из вершины прямого угла С прямоугольного треугольника АВС проведен перпендикуляр СS к плоскости АВС (рис. 533). Сравните катеты АС и ВС, если угол наклона наклонной SA к плоскости ABC больше угла наклона наклонной SB к этой плоскости.
468 |
Перпендикулярность прямых и плоскостей |
3. Из вершини В квадрата ABCD проведен перпендикуляр BS к плоскости ABCD (рис. 534). Сравните углы между плоскостя- ми ASD и CSD и плоскостью ABC.
4. На рис. 535 изображен равносторонний треугольник АВС, точка О — его центр,
D — середина BC, OP — перпендикуляр
к плоскости ABC. Величина какого угла
является углом между плоскостями:
1) BPC и ABC;
2) APO и BPO?
Задачи
|
|
|
||||
480. |
Пусть KS — перпендикуляр к плоскости квадрата ABCD, где |
|||||
|
K |
— середина стороны AD; KS = |
3 |
см, AB = 3 см. |
||
|
1°) Найдите угол между прямой SD |
и плоскостью ABC. |
||||
|
2°) Найдите угол между прямой BS |
и плоскостью ACD. |
||||
|
3°) Определите взаимное расположение плоскостей ABD и KCS. |
|||||
|
4) |
Найдите угол между прямой, проходящей через точку K и |
||||
|
середину стороны BC, и плоскостью |
BCS. |
|
|||
|
5) |
Найдите расстояние от точки B до прямой CS. |
||||
481. |
Из вершины A квадрата ABCD |
со стороной |
3 см проведен |
|||
|
перпендикуляр AS к плоскости квадрата длиной 3 см. |
|||||
|
1°) Найдите угол между прямой BS |
и плоскостью ABC. |
||||
|
2°) Найдите угол между прямой CS |
и плоскостью ABC. |
||||
|
3°) Определите взаимное расположение плоскостей ABS и |
|||||
|
BDC. |
|
|
|
||
|
4) |
Найдите угол между прямой CS и плоскостью ASD. |
||||
|
5) |
Найдите расстояние от точки B до прямой CS. |
||||
482°. Из вершины прямого угла А треугольника АВС проведен пер- |
||||||
|
пендикуляр АР к плоскости треугольника длиной 4 см. Катет |
|||||
|
AC равен 4 см, а угол АСВ — 60°. Найдите угол: |
|||||
|
1) |
между прямой РВ и плоскостью АВС; |
|
|||
|
2) |
между прямой РВ и плоскостью APC. |
|
|||

Измерение углов в пространстве |
469 |
483.Из центра О квадрата ABCD со стороной длиной 8 см восстав- лен перпендикуляр ОР так, что угол между прямой PC и плос- костью АВС равен 60°.
1°) Найдите углы между прямой PD и плоскостями АВС и АРС. 2°) Сравните углы, образованные прямыми РА, РВ, РС, РD с плоскостью АВС.
3°) Найдите расстояние от точки Р до плоскости АВС.
4)Докажите, что точки А и С симметричны относительно плос- кости PBD.
484.Дан куб AВCDA1B1C1D1 с ребром а.
1)Найдите угол между диагональю В1D и плоскостью ACC1.
2)Сравните углы, образованные диагональю B1D с плоскостя- ми его граней.
3)Найдите угол между диагональю B1D и плоскостью А1C1D.
4)Найдите расстояние от точки D1 до плоскости A1C1D.
485.Равнобедренный треугольник АВС с высотой 16 см, проведен- ной к его основанию, перегнули по средней линии MN, парал- лельной основанию AC, так, что вершина B удалена от плоскос- ти четырехугольника ACNM на 4 см.
1°) Найдите угол между плоскостями AMC и MBN.
2°) Постройте линейный угол двугранного угла BMNC и найдите его угловую меру, если ортогональная проекция вершины B на плоскость четырехугольника AMNC лежит за его пределами.
3°)СравнитеугловыемерыдвугранногоуглаBMNC иуглаBMA. 4°) Найдите расстояние от точки B до прямой AC.
5)Найдите расстояние от прямой MN до плоскости ABC.
6)Постройте линию пересечения плоскостей AMB и BNC.
486.Квадрат АВСD со стороной 4 2 см перегнули по прямой, про- ходящей через середины M и N сторон DC и BC так, что верши- на C удалена от плоскости AMN на 1 см.
1°) Найдите угол между плоскостями ADM и CMN.
2°) Постройте линейный угол двугранного угла BMNC и найди- те его угловую меру, если ортогональная проекция вершины C на плоскость пятиугольника ABNMD лежит за его пределами. 3°) Сравните угловые меры двугранного угла BMNC и угла CNB. 4°) Найдите расстояние от точки C до прямой BD.
5)Найдите расстояние от прямой MN до плоскости BDC.
6)Постройте линию пересечения плоскостей BNC и DMC. 487°. Из вершины квадрата АВСD проведен перпендикуляр АР к
плоскости квадрата.
1)Докажите, что угол РВА является линейным углом двугран- ного угла РВСА.
470 |
Перпендикулярность прямых и плоскостей |
2) Сравните угловые меры двугранных углов РВСА и РCDA. 3) Найдите угол между плоскостями АРВ и АРD.
488. Два одинаковых равнобедренных треугольника АВС и АВD с общим основанием АВ лежат в различных плоскостях; K — се- редина АВ.
1°)Докажите,чтоСKD—линейныйуголдвугранногоуглаСАВD. 2) Постройте линейный угол двугранного угла DACB.
3) Сравните угловые меры двугранных углов CABD и ACDB, если АВ = СD.
489. Дан куб AВCDA1B1C1D1; М — середина ребра АА1. Вычислите: 1) угол между диагональю грани А1В1С1 и плоскостью MDB; 2) углы между прямой МC1 и плоскостями А1B1D1, ВCC1, DBD1; 3) угол между прямыми МC1 и ВС.
490°. Длина ручки швабры равна 1,2 м.
1) На каком расстоянии от пола размещен конец швабры при вытирании пола, если швабра наклонена к нему под углом
60°?
2) Какой угол образует ручка швабры с полом, если конец руч- ки удален от пола на 0,6 м?
491°. Канатная дорога в течение 15 мин поднимает лыжника на вер- шину горы от ее подножия со скоростью 2 м/с. Определите высоту горы, считая, что угол наклона горы приблизительно равен 30°.
492*. Пользуясьзаконамиотражениясвета,докажите,чтопадающий и отраженный лучи образуют с зеркалом одинаковые углы.
493°. Точка М лежит между гранями двугранного угла и удалена от каждой из них на 8 см. Найдите расстояние от точки М до ребра, если величина двугранного угла равна: 1) 90°; 2) 60°; 3) 120°.
494°. Найдите угловую меру двугранного угла, если точка, лежащая на одной грани, расположена от ребра на расстоянии, вдвое большем, чем от второй грани.
495. Угол падения угольного пласта равен 35°. При вертикальном бурении обнаружено, что длина пути бура в угле равна 2,2 м. Вычислите толщину пласта.
496*. Прямая а образует равные углы с тремя прямыми, лежащими в плоскости α и проходящими через точку пересечения прямой а с плоскостью α. Докажите, что а α.
497*. Из вершины В ромба АВСD проведен перпендикуляр ВK к его плоскости. Сторона ромба равна а, острый угол при вершине А равен α, а длина перпендикуляра — b. Найдите:
1) расстояние от точки А до плоскостей KDВ; KВС; KDС; 2) углы между прямой АK и прямыми СD; ВD;
3) угол между прямой АK и плоскостью ВDK;
4)углымеждуплоскостямиАВKиKВС;АDKиDKС;АВKиDKС.

Измерение углов в пространстве |
471 |
Итог
Основные определения
Углом между пря мой и неперпен
дикулярной к ней плоскостью назы-
вается угол между прямой и ее ортого- нальной проекцией на эту плоскость.
Углом между дву
мя пересекающи
мися плоскостя ми называется угол между прямыми, образованными при пересечении данных плоскостей третьей плоскостью, перпен- дикулярной линии пересечения первых двух.
Фигура,образованная двумя полуплоскостя- ми, выходящими из одной прямой, назы-
вается двугранным углом. Общая пря- мая полуплоскостей называется ребром, а сами полуплоскос-
ти — гранями дву
гранного угла.

Готовимся к тематическому
контролю по теме «Перпендикулярность прямых и плоскостей»
?Задания для самоконтроля
1.Сторона АВ правильного треугольника АВС лежит в плоскости α. Всегда ли высота СD этого треугольника перпендикулярна плоскости α?
2.Можно ли утверждать, что прямая, перпендикулярная диаметру окружности, перпендикулярна и её плоскости?
3.Можно ли с помощью двух прямоугольных пластин определить направление, перпендикулярное плоскости стола?
4.Существует ли такая прямая, через которую можно провести бесконечное множество плоскостей, перпендикулярных данной плоскости?
5.Могут ли две прямые быть перпендикулярными некоторой плоскости и пересекаться?
6.Могут ли быть параллельными две плоскости, если известно, что только одна из них перпендикулярна данной прямой?
7.Имеют ли одинаковую форму сечения куба, перпендикулярные его диагонали?
8.Верно ли, что две различные плоскости, перпендикулярные одной прямой, не имеют общих точек?
9.Перпендикулярны ли две плоскости, если они перпендикулярны третьей плоскости и линии их пересечения с этой плоскостью перпендикулярны между собой?
10.Может ли ортогональной проекцией острого угла быть развернутый угол?
11.Могут ли быть равными ортогональные проекции двух неравных наклонных?
12.Основание перпендикуляра, проведенного из данной точки к плоскости ромба, не являющегося квадратом, совпадает с точкой пересечения диагоналей ромба. Может ли данная точка быть равноудаленной от вершин ромба?
Готовимсяк тематическому контролю по теме |
473 |
13.Могут ли две наклонные различной длины быть одинаково наклоненными к плоскости?
14.Может ли угол между плоскостями равняться 100°?
15.Всегда ли можно к невертикальному столбу прикрепить вер- тикально щит?
Образец контрольной работы
Из центра О правильного треугольника АВС со стороной 2 см проведен перпендикуляр OS длиной 2 см.
1°) Определите взаимное расположение прямой АВ и плос- кости OCS.
2°) Определите взаимное расположение плоскостей OSC
и АВС.
3°) Найдите расстояние от точки А до плоскости OSC. 4°) Найдите угол между прямой SC и плоскостью АВС. 5°) Найдите угол между плоскостями SВC и АВС.
6) Постройте плоскость, проходящую через середину отрезка АS параллельно плоскости SВC, и найдите расстояние меж- ду этими плоскостями.
|
|
Ответы к заданиям для самоконтроля |
|
|
||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
Нет Нет |
Да |
Да Нет Нет Нет Да |
Да |
Да |
Да |
Нет |
Да |
Нет |
Да |
|||||
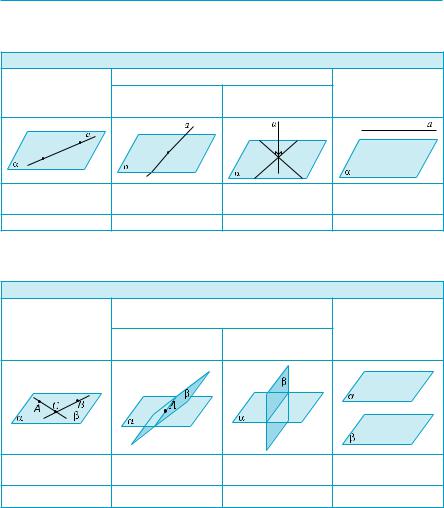
|
Взаимное расположение двух прямых в пространстве |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 40 |
||
|
|
|
|
Количество общих точек |
|
|
|
|
||||||
Не менее |
|
|
Одна |
|
|
|
|
Нет |
|
|
||||
|
Общий |
|
|
Частный |
|
Лежат |
Не лежат |
|||||||
|
двух |
|
|
|
|
в одной |
в одной |
|||||||
|
|
|
случай |
|
|
случай |
|
|||||||
|
|
|
|
|
|
|
плоскости |
плоскости |
||||||
|
|
|
|
|
|
|
|
|
||||||
|
а и b |
|
а и b пере- |
а и b — пер- |
а и b — |
а и b — |
|
|||||||
|
|
пендику- |
скрещиваю- |
|||||||||||
совпадают |
|
секаются |
|
параллельны |
||||||||||
|
|
|
|
|
|
|
лярны |
|
|
|
|
|
щиеся |
|
|
a=b |
|
|
a × b |
|
|
а b |
|
|
a || b |
|
|
a · b |
|
474 |
Перпендикулярность прямых и плоскостей |
||
Взаимное расположение прямой и плоскости |
|||
|
|
|
Таблиця 41 |
|
Количество общих точек |
|
|
Не менее двух |
Одна |
Нет |
|
Общий |
Частный случай |
||
|
случай |
|
|
|
|
|
|
а принадлежит α |
а пересекает α |
а и α — пер- |
а параллельна α |
пендикулярны |
|||
а α |
а × α |
a α |
а || α |
Взаимное расположение двух плоскостей |
||||
|
|
|
Таблица 42 |
|
|
Количество общих точек |
|
||
Не менее трёх, |
Не менее одной, но все они лежат на |
|
||
одной прямой |
|
|||
не лежащих на |
Нет |
|||
Общий |
|
|||
одной прямой |
Частный случай |
|
||
случай |
|
|||
|
|
|
||
α и β |
α и β |
α и β — пер- |
α и β — |
|
совпадают |
пересекаются |
пендикулярны |
параллельны |
|
α = β |
α × β |
α β |
α|| β |
|
