§20. Перпендикулярность плоскостей

Ðассматривается отношение перпендикулярности плоскостей — одно из важнейших и наиболее используемых в геометрии пространства и ее приложениях.

Из всего разнообразия взаимного расположения

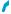
двух плоскостей особого внимания и изучения заслуживает то, при котором плоскости перпендикулярны друг другу (например, плоскости смежных стен комнаты,

забора и участка земли, двери и пола и т. п. (рис. 417, а–в).

Приведенные примеры позволяют увидеть одно из основных свойств отношения, которое мы будем изучать, — симметричность расположения каждой из плоскостей относительно другой. Симметрия обеспечивается тем, что плоскости вроде бы «сотканы» из перпендикуляров. Попробуем уточнить эти наблюдения.

Пусть имеем плоскость α и прямую с на ней (рис. 418, а). Проведем через каждую точку прямой с прямые, перпендикулярные плоскости α. Все эти прямые параллельны между собой (почему?) и составляют, на основании задачи 1 § 8, некоторую плоскость β (рис. 418, б). Естественно назвать плоскость β перпендикуляр­ ной плоскости α.

В свою очередь, все прямые, лежащие в плоскости α и перпен- дикулярные прямой с, образуют плоскость α и перпендикулярны плоскости β (рис. 418, в). Действительно, если а — произвольная такая прямая, то она пересекает прямую с в некоторой точке М. Через точку М проходит в плоскости β перпендикулярная α пря- мая b, поэтому b а. Следовательно, а с, а b, поэтому а β. Таким образом, плоскость α перпендикулярна плоскости β, а пря- мая с является линией их пересечения.

Две плоскости называются перпендикулярными, если каждая из них образована прямыми, перпенди­ кулярными второй плоскости и проходящими через точки пересечения этих плоскостей.

Перпендикулярностьплоскостейαиβобоз- начается привычным уже знаком: α β.

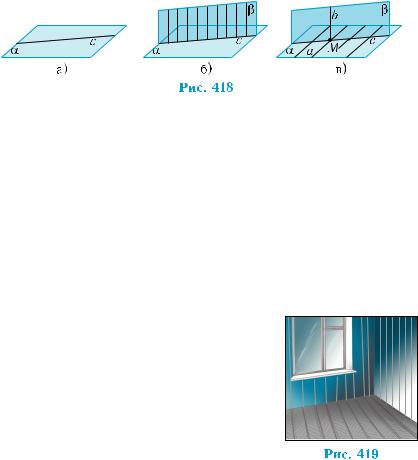
Одну из иллюстраций этого определения можно представить, если рассмотреть фраг- мент комнаты дачного домика (рис. 419). В нем пол и стена сложены из досок, перпен- дикулярных соотвественно стене и полу. По- этому они перпендикулярны. На практике

это означает, что пол горизонтален, а стена вертикальна.

Приведенное определение трудно использовать при фактичес- кой проверке перпендикулярности плоскостей. Но если внима- тельно проанализировать рассуждения, которые привели к этому определению, то видим, что перпендикулярность плоскостей α и β обеспечило наличие в плоскости β прямой b, перпендикулярной плоскости α (рис. 418, в). Мы пришли к признаку перпендику- лярности двух плоскостей, который чаще всего применяется на практике.

406 Перпендикулярность прямых и плоскостей

Теорема 1 (признак перпендикулярности плоскостей).

Если одна из двух плоскостей проходит через прямую, перпендикулярную второй плоскости, то эти плоскости перпендикулярны.

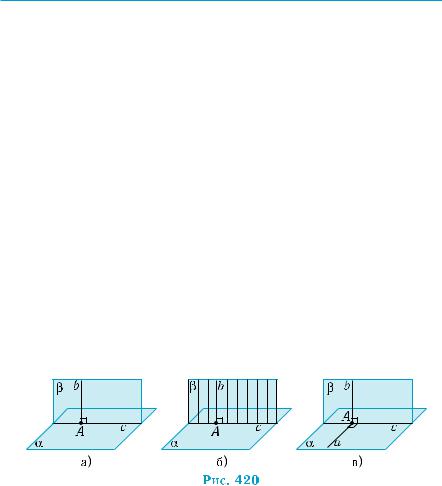
 Пусть плоскость β проходит через прямую b, перпендику- лярную плоскости α и с — линия пересечения плоскостей α и β (рис. 420, а). Все прямые плоскости β, параллельные прямой b и пересекающие прямую с, вместе с прямой b образуют плоскость β. По теореме о двух параллельных прямых, одна из которых пер- пендикулярна плоскости (теорема 1 § 19), все они вместе с прямой b перпендикулярны плоскости α. То есть плоскость β состоит из прямых, проходящих через линию пересечения плоскостей α и β и перпендикулярных плоскости α (рис. 420, б).

Теперь в плоскости α через точку А пересечения прямых b и с проведем прямую а, перпендикулярную прямой с (рис. 420, в). Прямая а перпендикулярна плоскости β, по признаку перпен- дикулярности прямой и плоскости (а с, по построению, а b, так как b α). Повторив предыдущие рассуждения, получим, что плоскость α состоит из прямых, перпендикулярных плоскости β, проходящих через линию пересечения плоскостей. Согласно оп- ределению, плоскости α и β перпендикулярны. ■

Приведенный признак дает возможность устанавливать пер- пендикулярность плоскостей или же обеспечивать ее.

П р и м е р 1 . Прикрепить щит к столбу так, чтобы он был распо- ложен вертикально.

 Если столб стоит вертикально, то достаточно приложить произвольно щит к столбу и закрепить его (рис. 421, а). Согласно рассмотренному выше признаку, плоскость щита будет перпенди- кулярна поверхности земли. В этом случае задача имеет беско- нечное множество решений.

Если же столб стоит наклонно к земле, то достаточно к столбу прикрепить вертикальную рейку (рис. 421, б), а затем щит при- крепить и к рейке, и к столбу. В этом случае положение щита бу- дет вполне определённым, поскольку столб и рейка определяют единственную плоскость. ■

В предыдущем примере «техническое» задание свелось к мате- матической задаче о проведении через данную прямую плоскос- ти, перпендикулярной другой плоскости.

П р и м е р 2 . Из вершины A квадрата ABCD проведен перпен- дикулярный его плоскости отрезок AK, AB = AK = а.

1) Определить взаимное расположение плоскостей AKC и ABD,

AKD и ABK.

2) Построить плоскость, проходящую через прямую BD перпенди- кулярно плоскости ABC.

3) Провести через середину F отрезка KC плоскость, перпендику- лярную плоскости KAC.

4) Найти площадь треугольника BDF.

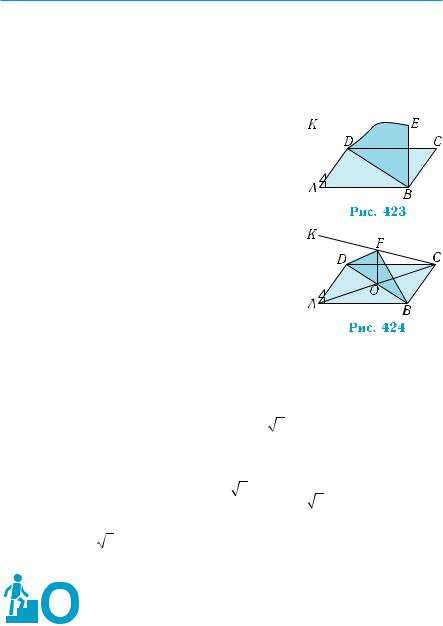
 Построим рисунок, соответствующий условию примера (рис. 422).

1) Плоскости AKC и ABD перпендикуляр- ны, по признаку перпендикулярности плос- костей (теорема 1): AK ABD, по условию. Плоскости AKD и ABK также перпендику-

лярны, по признаку перпендикулярности плоскостей (теорема 1). Действительно, прямая AB, через кото- рую проходит плоскость ABK, перпендикулярна плоскости AKD, по признаку перпендикулярности прямой и плоскости (теорема 1 § 18): AВ AD, как смежные стороны квадрата; AВ AK, так как

AK ABD.

2) По признаку перпендикулярности плоскостей, для искомого построениядостаточночерезнекоторуюточкупрямойBD провести

408 Перпендикулярность прямых и плоскостей

прямую, перпендикулярную плоскости ABC. А для этого достаточ- но через эту точку провести прямую, параллельную прямой AK.

Действительно, по условию, прямая AK перпендикулярна плос- кости ABC и потому, согласно теореме о двух параллельных пря-

Теорема 2 (о перпендикуляре к линии пересечения перпенди- кулярных плоскостей).

Если две плоскости перпендикулярны, то прямая, принадлежащая одной плоскости и перпендикулярная линии пересечения этих плоскостей, перпендикулярна второй плоскости.

 Пусть перпендикулярные плоскости

α и β пересекаются по прямой с, а прямая b в плоскости β перпендикулярна прямой с и пересекает ее в точке В (рис. 425). По опре-

делению перпендикулярности плоскостей, в плоскости β через точку В проходит прямая

b1,перпендикулярная плоскости α. Понятно, что она перпендикулярна прямой с. Но че-

рез точку прямой в плоскости можно провес- ти лишь одну прямую, перпендикулярную данной прямой. Поэтому

прямые b и b1 совпадают. А это означает, что прямая одной плоскос- ти, перпендикулярная линии пересечения двух перпендикулярных плоскостей, перпендикулярна второй плоскости. ■

Применим рассмотренную теорему к обоснованию еще одного признака перпендикулярности плоскостей, важного с точки зре- ния последующего изучения взаимного расположения двух плос- костей.

Пустьплоскостиαиβперпендикулярны, прямая с — линия их пересечения. Через произвольную точку А прямой с проведем

в плоскостях α и β прямые а и b, перпен- дикулярные прямой с (рис. 426). По теоре-

ме 2, прямые а и b перпендикулярны соот- ветственно плоскостям β и α, поэтому они перпендикулярны между собой: а b. Пря-

мые а и b определяют некоторую плоскость γ. Линия пересечения с плоскостей α и β

перпендикулярна плоскости γ, по признаку перпендикулярности прямой и плоскости (теорема 1 § 18): с а, с b, а γ, b γ. Если учесть произвольность выбора точки А на прямой с и тот факт, что через точку А прямой с проходит единственная плоскость, ей перпендикулярная, то можно сделать следующий вывод.

Теорема 3 (о плоскости, перпендикулярной линии пересече- ния перпендикулярных плоскостей).

Плоскость, перпендикулярная линии пересечения двух перпендикулярных плоскостей, пересекает эти плоскости по перпендикулярным прямым.

Таким образом, установлено еще одно свойство перпендику- лярных плоскостей. Это свойство является характеристическим, то есть если оно справедливо для некоторых двух плоскостей, то плоскости перпендикулярны между собой. Имеем еще один при- знак перпендикулярности плоскостей.

Теорема 4 (второй признак перпендикулярности плоскос- тей).

Если прямые пересечения двух плоскостей третьей плоскостью, перпендикулярной линии их пересечения, перпендикулярны, то данные плоскости тоже перпендикулярны.

Пусть плоскости α и β пересекаются по прямой с, и плоскость γ, перпендикулярная прямой с, пересекает плоскости α и β соот-

ветственно по прямым а и b (рис. 427). По условию, а b. Поскольку γ с, то а с. А поэтому прямая а перпендикулярна плос- кости β, по признаку перпендикулярности прямой и плоскости (теорема 1 § 18). Отсю-

да вытекает, что плоскости α и β перпенди- кулярны, по признаку перпендикулярнос- ти плоскостей (теорема 1). ■

Заслуживают внимания и теоремы о связях перпендикуляр- ности двух плоскостей третьей плоскости с их взаимным распо- ложением.

Теорема 5 (о линии пересечения двух плоскостей, перпендику- лярных третьей плоскости).

Если две плоскости, перпендикулярные третьей плоскости, пересекаются, то линия их пересечения перпендикулярна этой плоскости.

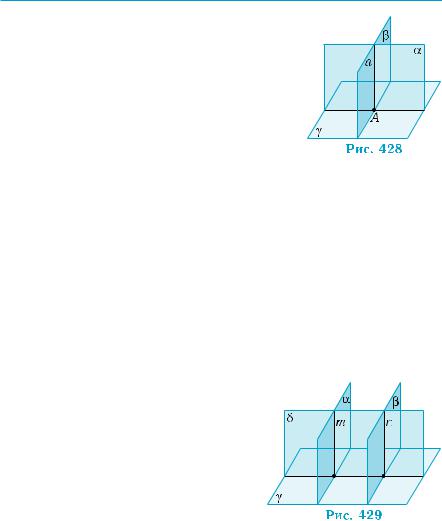
 Пусть плоскости α и β, перпендикулярные плоскости γ, пере- секаются по прямой а (a || γ), и А — точка пересечения прямой а с

Рассмотрим теорему, описывающую связь между параллель- ностью и перпендикулярностью плоскостей. Соответствующий ре- зультат мы уже имели для прямых и плоскостей.

Теорема 6 (о параллельных плоскостях, перпендикулярных третьей плоскости).

Если одна из двух параллельных плоскостей перпендикулярна третьей, то и вторая плоскость перпендикулярна ей.

 Пусть плоскости α и β парал- лельны, а плоскость γ перпендикуляр- на плоскости α. Поскольку плоскость γ

пересекает плоскость α, то она должна пересекать и параллельную ей плос- кость β. Возьмем в плоскости α про-

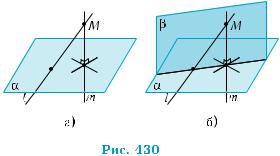
извольную прямую m, перпендику- лярную плоскости γ, и проведем через нее, а также через произвольную точ- ку плоскости β, плоскость δ (рис. 429).

Плоскости δ и β пересекаются по прямой п, а поскольку α ║β, то т║п (теорема 2 §18). Из теоремы 1 вытекает, что п γ, а потому перпендикулярной плоскости γ будет и плоскость β, проходящая через прямую п. ■

Доказанная теорема дает еще один признак перпендикуляр- ности плоскостей.

Далее рассмотрим ряд задач на построение перпендикулярных плоскостей.

Через заданную точку провести плоскость, перпендикулярную данной, можно с помощью признака перпендикулярности плоскос- тей (теорема 1). Достаточно через эту точку провести прямую, пер- пендикулярную данной плоскости (см. задачу 1 § 19). А затем через построеннуюпрямуюпровестиплоскость.Онабудетперпендикуляр- ной данной плоскости по указанному признаку. Понятно, что таких плоскостей можно провести бесконечное множество.

Более содержательной является задача о построении плоскос- ти, перпендикулярной данной, при условии, что она проходит че- рез данную прямую. Понятно, что если данная прямая перпенди- кулярна данной плоскости, то таких плоскостей можно построить бесконечное множество. Осталось рассмотреть случай, когда дан- ная прямая не перпендикулярна данной плоскости. Возможность такого построения обоснована на уровне физических моделей прямых и плоскостей в примере 1.

З а д а ч а 1 . Доказать, что через произвольную прямую, не пер- пендикулярную плоскости, можно провести плоскость, перпенди- кулярную данной плоскости.

Пусть даны плоскость α и прямая l, l B\ a. Возьмём на прямой l произвольную точку М и проведем через нее прямую т, перпен- дикулярную плоскости α (рис. 430, а). Поскольку, по условию, l не перпендикулярна α, то прямые l и т пересекаются. Через эти прямые можно провести плоскость β (рис. 430, б), которая, соглас- но признаку перпендикулярности плоскостей (теорема 1), будет перпендикулярной плоскости α. ■

П р и м е р 3 . Через вершину А правильной пирамиды SABC с основанием ABC провести прямую, перпендикулярную плоскости боковой грани SBC.

 Для решения данной задачи воспользуемся теоремой о пер- пендикуляре к линии пересечения перпендикулярных плоскостей

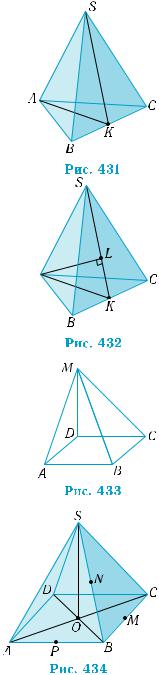
(теорема 2). Пусть K — середина ребра BC (рис. 431). Плоскости AKS и BCS перпенди- кулярны, по признаку перпендикулярнос- ти плоскостей (теорема 1). Действительно, ВС SK и ВС АK, как медианы, проведен- ные к основаниям в равнобедренных тре­ угольниках. Поэтому, по признаку перпенди- кулярности прямой и плоскости (теорема 1 §18), прямая ВС перпендикулярна плоскости AKS. Плоскость BCS проходит через прямую, перпендикулярную плоскости AKS.

Построение. Проведем в плоскости AKS из точки A прямую AL, перпендикулярную прямой KS — линии пересечения плоскостей AKS и BCS (рис. 432). По теореме о перпен- дикуляре к линии пересечения перпендику- лярных плоскостей (теорема 2), прямая AL 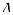перпендикулярна плоскости BCS. ■

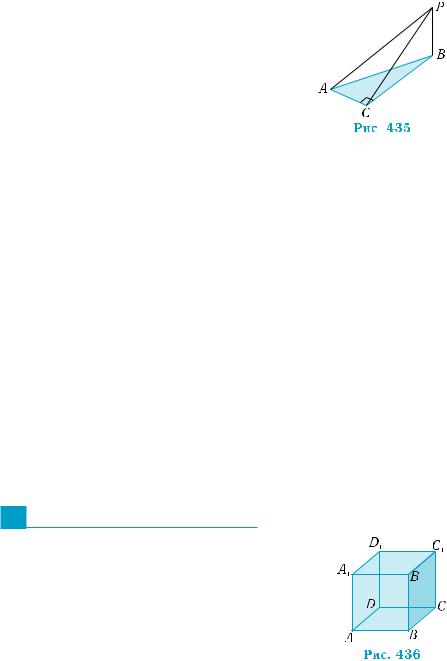
2.На рис. 434 изображена правиль- ная четырехугольная пирамида

SABCD, точки P, M, N — середи-

ны рёбер AB, BC, BS, O — центр основания ABCD. Какие из пар плос- костей перпендикулярны:

1)ACS и BDS; 2) MOS и POS;

3)COS и MNP; 4) MNP и SOB;

5)CND и ABS?

3) PAC и PBC; 4) PAC и PAB?

4.Две плоскости перпендикулярны. Можно ли через произвольную точку одной из них провести прямую в этой плоскости, второй плоскости?

5.В плоскости α нельзя провести прямую, плоскости β. Могут ли эти плоскости быть ми?

6.Через некоторую точку плоскости α проходит щая в этой плоскости и перпендикулярная плоскости ли, что плоскости α и β перпендикулярны?

Секция забора прикреплена к вертикальному столбу ли утверждать, что плоскость забора вертикальна?

Как к рейке, параллельной поверхности земли, прикрепить вертикально щит?

Почему поверхность дверей, независимо от того, закрыты они или открыты, располагается вертикально к полу?

Почему отвес плотно прилегает к вертикальной стене, а к на- клонной — не обязательно?

Можно ли к наклонному столбу прикрепить щит так, чтобы он был перпендикулярен поверхности земли?

Как на практике установить, перпендикулярна ли плоскость

стены плоскости пола? перпендикулярнуюперпендикулярнуюперпендикулярны-прямая, лежа-β. Верно7. . Можно8.9.10.11.12.

Графические упражнения

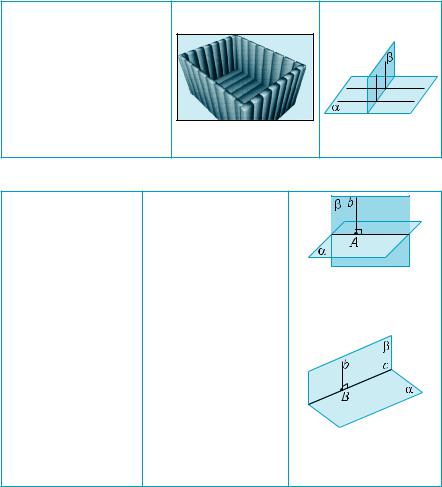
1.На рис. 436 изображен куб ABCDA1B1C1D1.

1)Укажите плоскости, перпендикулярные плоскости ВDD1.

2)Как расположены плоскости и

? A1B1CAB1C1

Задачи

421. Отрезок OS проведен из центра О квадрата ABCD перпен- дикулярно его плоскости.

1°) Определите взаимное расположение плоскостей ACS

и АВС.

2°) Определите взаимное расположение плоскостей ACS

и BDS .

3) Постройте плоскость, проходящую через прямую OS пер- пендикулярно плоскости ABS.

4) Постройте плоскость, перпендикулярную плоскости АВС и проходящую через середины сторон AD и CD.

422. Из точки пересечения O диагоналей ромба ABCD проведен перпендикулярный плоскости ромба отрезок OS; AB = DB =

= SA = а.

1°) Определите взаимное расположение плоскостей SDB и

ABC, SDB и ACS.

2°) Постройте плоскость, проходящую через прямую BC пер- пендикулярно плоскости ABD.

3) Проведите через середину F отрезка CS плоскость, пер- пендикулярную плоскости АВС.

4) Найдите площадь треугольника BDF.

423. Дан куб ABCDA1B1C1D1.

1°) Определите взаимное расположение плоскостей АВ1С1

и CDD1.

2°) Определите взаимное расположение плоскостей АВ1С1

и CD1A1.

3°) Постройте плоскость, проходящую через точку А перпен- дикулярно плоскости BB1D1.

4) Постройте сечение куба плоскостью, проходящей через се- редины рёбер А1D1 и B1C1 перпендикулярно плоскости АВС. 5)ОпределитевзаимноерасположениеплоскостиАА1Виплос- кости, проходящей через середины рёбер А1В1, C1D1, CD.

6) Найдите площадь сечения куба плоскостью, проходящей через ребро ВВ1 и середину ребра A1D1 (ВВ1 = а).

7) Постройте точку, симметричную точке А относительно плоскости A1B1C.

424. В правильном тетраэдре АBCD с ребром 2 см точка М — се- редина DВ, а точка N — середина АС.

1°) Докажите, что прямая DВ перпендикулярна плоскости

АМС.

2°) Докажите, что плоскость ВDМ перпендикулярна плос- кости АМС.

3) Через точку О пересечения медиан треугольника АDС проведите прямую, перпендикулярную плоскости АМС.

4) Найдите длину отрезка этой прямой внутри тетраэдра. 5) В каком отношении плоскость АМС делит этот отрезок?

425. Два равносторонних треугольника АВС и ADC лежат в пер- пендикулярных плоскостях.

1°) Найдите длину отрезка BD, если AC = 1 см.

2) Докажите, что плоскость BKD (K лежит на прямой AC) перпендикулярна плоскости каждого из треугольников тог- да и только тогда, когда K является серединой стороны AC.

426. Прямоугольник ABCD, стороны которого 3 см и 4 см, пере- гнули по диагонали AC так, что треугольники ABC и ADC расположились в перпендикулярных плоскостях. Опреде- лите расстояние между точками B и D после того, как пере- гнули прямоугольник ABCD.

427. Через данную точку проведите плоскость, перпендикуляр- ную каждой из двух данных плоскостей.

428°. Докажите, что плоскости смежных граней куба перпендику- лярны.

429. Плоскости α и β перпендикулярны между собой. Из точки А плоскости α проведена перпендикулярная плоскости β пря- мая АВ. Докажите, что прямая АВ лежит в плоскости α.

430. Докажите, что если плоскость и прямая, не лежащая в этой плоскости, перпендикулярны одной и той же плоскости, то они параллельны между собой.

431. Через точки А и В, лежащие на линии пересечения р пер- пендикулярных между собой плоскостей α и β, проведены перпендикулярные р прямые: АА1 в α, ВВ1 в β. Точка X ле- жит на прямой АА1, а точка Y — на ВB1. Докажите, что пря- мая ВB1 перпендикулярна прямой ВХ, а прямая АA1 пер- пендикулярна прямой АY.

432*.Через середину каждой стороны треугольника проведена плоскость, перпендикулярная этой стороне. Докажите, что все три проведенные плоскости пересекаются по одной пря- мой, перпендикулярной плоскости треугольника.

Упражнения для повторения

433.В равностороннем треугольнике со стороной b определите: 1) высоту; 2) радиусы вписанной и описанной окружностей.

434.Из одной точки проведен к данной прямой перпендикуляр и две наклонные. Определите длину перпендикуляра, если наклонные равны 41 см и 50 см, а их проекции на данную прямую относятся, как 3 : 10.

435.Определите катеты прямоугольного треугольника, если бис- сектриса прямого угла делит гипотенузу на отрезки 15 см и

20 см.

Итог

Основное определение

Две плоскости называ-

ются перпендикуляр­ ными, если каждая из них образована прямы- ми, перпендикулярны- ми второй плоскости и проходящими через точки пересечения этих плоскостей.