9. РАСХОЖДЕНИЕ ИЗМЕНЕНИЕМ СКОРОСТИ
9.1. Характеристика маневров скоростью
Маневр скоростью в общем случае не является основным для расхождения и должен выполняться, если изменение курса малоэффективно либо затруднено вследствие ограниченности района маневрирования (акватория порта, узкость, фарватер) или наличия препятствий со стороны других судов. Этот маневр требует заблаговременной подготовки энергетической установки к изменению хода судна. Ситуации, в которых двигатель должен быть переведен в маневренный режим, оговариваются в руководствах по штурманской службе.
При выполнении рейсов стараются идти полным ходом или, при необходимости, сниженной максимальной безопасной скоростью. Поэтому в преобладающем большинстве случаев для устранения угрозы столкновения скорость меняется в меньшую сторону. Увеличение хода обычно используется после расхождения для возвращения к исходной скорости движения. Учитывая это, ниже считается, что для предупреждения столкновения судно оператора снижает ход.
Особенностью рассматриваемого маневра является большая продолжительность, что сказывается на точности прогноза ситуации на момент его окончания. Такой маневр должен начинаться раньше, чем поворот, и, чтобы быть заметным, выполняться переводом телеграфа сразу на 2-3 хода. При изменении курса судно остается управляемым, что оставляет возможность принять дополнительные меры для нейтрализации неблагоприятного маневра «цели» или других обстоятельств. При активном торможении управляемость существенно ухудшается, а когда используется режим заднего полного хода, судно обычно становится неуправляемым.
Маневр скоростью, как и циркуляция, неэффективен, когда приближающаяся опасная «цель» находится у судна оператора на небольшом курсовом угле [35]. Это наблюдается, когда курс судна оператора близок к контркурсу опасной «цели» либо когда ее скорость значительно меньше скорости СО.
В отличие от циркуляции, при маневре скоростью DCPA опасной «цели» увеличивается с ростом расстояния от точки инициации маневра до предельной точки его начала.
При выборе для расхождения изменения скорости следует определить:
-предельную точку начала маневра для безопасного расхождения с главной «целью»;
-степень риска столкновения с другими «целями» на момент окончания маневра и в процессе его выполнения.
При решении этих задач используется полученный по математической модели массив данных (табл. 9.1), отражающих изменение кинематических параметров СО в процессе маневра. При нормальной погоде для судна с
204
конкретной загрузкой значения этого массива определяются исходной скоростью VШ, новым значением хода VM , режимом работы двигателя
(РРД) при переходе к VM . Чтобы не загружать компьютер СПС излишними
расчетами, рационально получать характеризуемый массив эпизодически, только в случаях изменения его данных.
Таблица 9.1. Массив значений параметров движения судна в процессе изменения скорости
τ, сек. |
ξ |
ζ |
V |
S |
0 |
0 |
0 |
V0 |
0 |
1 |
ξ1 |
ζ1 |
V1 |
S1 |
2 |
ξ2 |
ζ2 |
V2 |
S2 |
… |
… |
… |
… |
… |
i |
ξi |
ζi |
Vi |
Si |
… |
… |
… |
… |
… |
τМ |
ξM |
ζM |
VM |
SM |
9.2. Общая часть задач определения границы безопасных маневров
Задача нахождения предельной точки начала маневра скоростью ставится следующим образом. Судно оператора, движущееся курсом KШ и
скоростью VШ, сближается с идущей постоянным курсом KJ и скоростью VJ «целью» J так, что существует угроза столкновения. Для ее устранения СО намерено снизить V до значения VM с использованием выбранного РРД.
Требуется определить граничную точку на линии пути СО, которая разделяет области начала безопасных и опасных маневров расхождения с «целью».
Выделяют два типа поставленной задачи [35]. Первый отвечает ситуации, когда при инициации маневра в граничной точке СО окажется на кратчайшем расстоянии до «цели» после его окончания, а второй – когда это происходит в процессе изменения скорости.
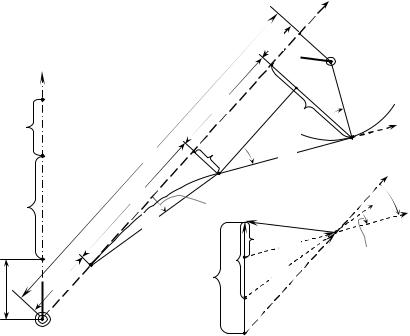
Решение названных типов задачи имеет общую часть. Для ее пояснения используется схема истинного и относительного движения СО при расхождении изменением V , представленная на рис. 9.1,а. В общую процедуру входят следующие операции.
1) По математической модели с выбранным шагом изменения τ получаются значения параметров (см. табл. 9.1) движения судна в процессе
торможения от VШ до VM , а также полное время τM маневра и пройденное за это время расстояние SM .
2) По SM , τM рассчитывается средняя скорость VE на участке торможения
205
VE = SM / τM . |
(9.1) |
kø
|
|
|
|
sγ |
d |
|
||
KØ |
|
|
|
|
KJ |
J |
|
|
Z |
|
|
sr |
|
rγ |
γ ds |
|
|
S |
|
|
|
|
|
kμ |
||
|
|
rδ |
γ |
|
z |
|||
C |
а) |
s |
s |
|||||
kø |
||||||||
|
c |
|
|
|
||||
|
|
sδ |
|
|
ke |
γ |
||
SM |
|
δ |
|
VJ |
||||
|
se |
VM |
|
kμ |
||||
А |
|
|
uμ |
|
|
|||
|
|
Ve |
δ |
|
||||
sa |
а |
|
|
ue |
|
|||
|
|
б) |
|
|||||
|
VØ |
|
|
|||||
SA |
|
|
|
uø |
|
|||
0 |
|
|
|
|
|
|
|
|
Рис. 9.1. Пояснение к решению задачи первого типа
3) По значениям KШ и VШ, KШ и VE , KШ и VM из «треугольников скоростей» (рис. 9.1,б) вычисляются параметры движения СО относительно
«цели» ( kш и uш, ke и ue , kμ и uμ ).
4) По элементам относительного движения СО определяются значения
следующих параметров (см. рис. 9.1,а) |
|
|
|||
|
|
se = ue τM ; |
|
(9.2) |
|
|
|
|
δ = ke −kш; |
|
(9.3) |
|
|
|
γ = kμ −kш; |
|
(9.4) |
|
rδ |
= se sin δ |
|
(9.5) |
|
|
|
|
; |
|
|
|
sδ = se cos δ |
|
|
||
r |
= d s cos γ ±d |
|
|
||
γ |
|
|
|
|
(9.6) |
|
s |
|
= d s sin γ |
; |
|
|
γ |
|
|
||
|
|
|
|
|
|
где знак «плюс» отвечает пересечению (при отсутствии маневра) курса «цели» по носу, а «минус» - по корме.
5) Находится разность
r = rγ −rδ.
В зависимости от нее определяется тип задачи ( r ≥ 0 - первый тип; r < 0 - второй тип).
206
9.3. Алгоритм задачи первого типа
Схема сближения судов, отвечающая первому типу задачи, представлена на рис. 9.1,а. Положение предельной точки начала маневра в этом случае находится следующим образом.
1) По алгоритму общей части решения задач первого и второго типа (см.
параграф 9.2) рассчитываются δ, |
γ, se , sγ , |
sδ , sr , rγ , rδ, r . |
||||
2) По значениям γ и r |
вычисляются (см. рис. 9.1,а) расстояния |
|||||
sr = |
r tgγ |
|
(9.7) |
|||
s |
|
|
|
. |
|
|
= r / sin γ |
|
|
||||
3) Находится время tμ и расстояние S |
до СРА на момент окончания |
|||||
маневра |
|
|
|
|
|
|
tμ = s |
/ uμ |
|
(9.8) |
|||
S |
=V |
t . |
|
|||
t |
μ |
|
|
|||
|
|
M |
|
|
|
|
Здесь учитывается, что после окончания «предельного» маневра |
||||||
дистанция dtμ кратчайшего |
сближения |
с |
«целью» должна быть равна |
|||
dμ = d s .
4) |
Рассчитывается перемещение sa по относительному курсу kш от |
|
места судна до предельной точки a начала маневра |
|
|
|
sa = s −sγ −sr −sδ. |
(9.9) |
5) |
Определяется время хода от текущего места до границы безопасных |
|
маневров |
|
|
|
tA = sa / uш. |
(9.10) |
6) Рассчитывается расстояние от его текущего места судна оператора до точки A начала маневра
SA =VШ tA .
7) По координатам текущего места судна оператора, его курсу KШ и значению SA вычисляются координаты точки A.
207