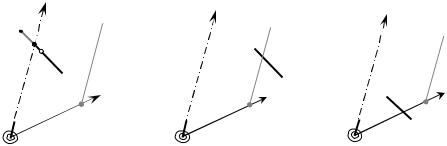
Рис. 7.4. Условия расположения МОМ

Взаключение можно отметить:

-«Цель», МОМ которой попадает на линию курса судна оператора, является опасной по d–критерию.

-Не представляющая угрозы «цель», метка или часть метки которой попадает в ОДМ, является лимитирующей В-маневр.

-Если линия пути СО проходит через метку ограничения в точке A (как на рис. 7.4,а), то расстояние кратчайшего сближения с «целью» равно

7.3. Погрешность в дистанции расхождения из-за пренебрежения инерционностью СО при В-маневре

Намечаемая траектория В-маневра рассматривается как маршрут судна для расхождения с «целью». При следовании по заданному маршруту для учета инерционности судна поворот начинается с упреждением, необходимым для точного выхода на новый отрезок пути. Выше при построении МОМ (см. параграфы 7.1, 7.2) повороты судна оператора считались мгновенными. Такое предположение приводит к погрешности прогноза положения «целей» на конец В-маневра. В результате при расхождении возникает несоответствие DCPA с дистанцией, намеченной по концам метки.

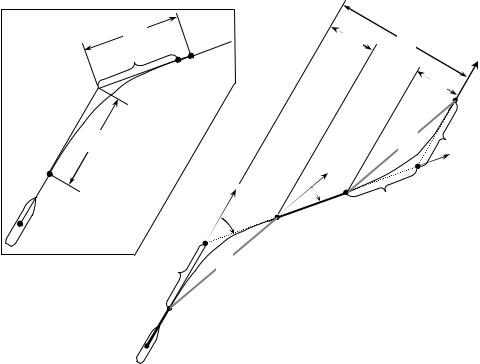
Траектория центра массы судна при изменении KШ на угол и показана на рис. 7.5,а, где

Sθ - расстояние до путевой точки CH , на котором надо начать поворот, чтобы точно выйти на линию нового курса;

Sθ2 - дистанция от CH до точки Cθ , в которой судно выходит на новый курс.

При автоматическом выполнении поворота Sθ2 обычно меньше, чем Sθ. Аналогичная картина наблюдается и при изменениях курса опытными рулевыми.

177

При планировании В-маневров с учетом динамики судна для удобства

концом поворота считается точка C2 . Она отстоит от CH на таком же расстоянии Sθ, как и точка C1 (см. рис. 7.5,а). Время tθ поворота и траекторию судна между точками C1 и C2 целесообразно находить моделированием движения. Дистанция C1C2 , проходимая судном при изменении курса, короче расстояния по ломаной линии C1CH C2 . Из-за этого продолжительность В-маневра будет меньше его времени, получаемого без

В табл. 7.1 для двух судов приведены параметры изменения курса с углом руля β =150 . По этим данным можно установить, что величина θt

может быть значительной.

Если по МОМ, полученной без учета инерционности СО, выбрать В-

маневр для расхождения на дистанции d s , то при пересечении курса «цели» по носу из-за меньшего времени поворота DCPA будет больше, а при

пересечении по корме – меньше, чем d s . Величина несоответствия зависит

178

от угла θ, соотношения скоростей и геометрии сближения судов. При больших углах θ она может достигать 5 кб.

Таблица 7.1.- Параметры, характеризующие В-маневр

Увеличение DCPA при пересечении курса «цели» по носу не оказывает отрицательного влияния на безопасность маневра в отличие от уменьшения DCPA при расхождении по корме. Для устранения несоответствия между планируемой и действительной DCPA, метка должна рассчитываться с учетом динамики СО.

Инерционность судна оператора ограничивает нижнюю границу ξ

полосы допустимых смещений. Чтобы при В-маневре нормально отработать два поворота в разные стороны на угол θ (см. рис. 7(.5,б), задаваемое

смещение ξ от линии пути должно быть больше величины ξ = 2 ξθ .

7.4. Определение меток ограничения В-маневра с учетом инерционности судна

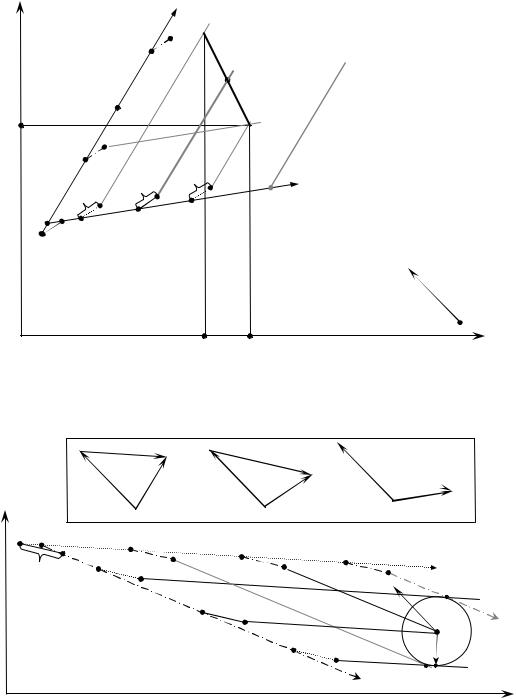
При рассмотрении алгоритма используются схемы, характеризующие истинное (рис. 7.6) и относительное (рис. 7.7) движение судна оператора при В-маневрах. На этих схемах криволинейные участки поворотов СО заменены

(см. рис. 7.5,б) эквивалентными по времени прямыми отрезками ( SE - на схеме истинного и se - на схеме относительного движения).

Алгоритм расчета с учетом инерционности СО положения МОМ включает следующие операции.

1)Моделированием поворота на угол θ находится траектория C1 C2 судна и параметры Sθ и tθ (см. рис. 7.5,а).

2)Криволинейные участки C1 C2 , C3 C4 (см. рис. 7.5,б) заменяется эквивалентными по времени прямыми отрезками длиной SE

179

Y KØ

YM M

A2

Рис. 7.6. Характеристика истинного движения СО при В-маневре

Рис. 7.7. Перемещения СО относительно «цели» при В-маневре

4) Решением «треугольников скоростей» (рис. 7.7,б) по формулам (7.2), (7.3) определяется относительный курс и скорость судна оператора:

kш uш - для движения СО курсом KШ и скоростью V ;

180

ks , us - для движения СО курсом KS и скоростью V ; ke , ue - для движения СО курсом KE и скоростью VE .

5) По ue и tθ вычисляется эквивалентное расстояние se , которое за

Эти соотношения отражают относительное перемещение СО по пути 0,ob ,b0 ,b3 ,J для сближения с «целью» вплотную (см. рис. 7.7,а).

7) Находится время tB2 следования СО от точки 0B до точки B2 и время τA движения от B2 до СРА из системы уравнений

Она составляется при рассмотрении относительного перемещения СО по

181