3.1. Деформации, перемещения

Деформацией тела называется изменение его формы или разме­ров, или того и другого одновременно, без изменения мас­сы тела.

Деформация тела обычно связана с изменением взаимного по­ло­­же­ния отдельных его точек (рис. 3.1). При этом линия, соединяю­щая две точ­ки тела, называется линейным элементом данного нап­ра­в­­ления (ab- в нап­равлении осиоxиac- в направлении осиоy, рис. 3.1).

Изменение длины линейного элемента называется абсолютной ли­­­нейной деформацией или абсолютным удлинением по данному на­п­­рав­лению.

Отношение изменения длины бесконечно малого линейного эле­мен­та 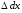к первоначальной его длине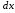называется относитель­ной линей­ной деформацией в точке по данному направлению.­

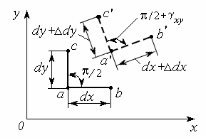
Рис. 3.1

Изменение прямого угла между двумя бесконечно малыми ли­ней­ными элементами, выходящими из одной точки, называется уг­лом сдвига в этой точке в плоскости линейных элементов.

Линейные и угловые деформации - величины безразмерные.

Изменение положения точки тела (изменение ее координат) в ре­зу­ль­та­те действия внешних сил называется линейным перемещением.

Вектор, проведенный из начального положения точки до дефор­ма­ции тела в конечное ее положение после деформации, называется пол­ным ли­ней­­ным перемещением этой точки. Проекция полного линейного пе­­ре­мещения точки на какое-либо направление называется ли­ней­ным перемещением точки по данному направлению.

Угол, составленный направ­ле­ни­­ем линейного элемента тела после деформации с его первоначальным направлением, на­зы­ва­ется угловым перемещением.

Приняты следующие обозначения для линейных и угловых де­фор­ма­ций:

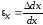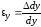- относительные линейные деформации по оси x-, по осиy - , по осиz-;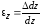

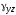- угловые деформации (сдвиги) в плоскости xoy-, в плос­ко­с­тиyoz-, в плоскостиzox-.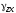

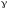Совокупность линейных деформаций по различным направ­ле­ни­ям и угловых деформацийпо различным плоскостям, прохо­дя­щим че­рез рассматриваемую точку, представляет собой деформи­ро­­ванное сос­­то­я­ние в точке.

Компоненты перемещений некоторой точки а, имею­щей до де­фор­­­ма­ции координатыx,y,z, обозначим черезu - по осиx, v - по осиy, w - по осиz. Эти компоненты линейного переме­ще­ния точки яв­ля­ются функ­ция­ми координат точкиа.

Перемещение соседней точки b, координаты которой отличают­ся от координат точкиaприращениямиdx,dy,dz, получим, разложив пе­ре­ме­ще­­­­ния в ряд Тейлора и ограничившись бесконечно малыми пер­во­го по­ря­д­­­ка:

,

,

.

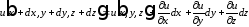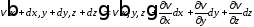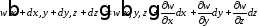3.2. Зависимости между деформациями и перемещениями. Формулы Коши

Бесконечно малый параллелепипед dxdydz, вырезанный из уп­ру­­гого тела около произвольной точки а, вследствие различия пе­ре­ме­щений его то­чек деформируется, т. е. изменяется длина его ребер и ис­кажаются пер­во­­начально прямые углы между гранями (рис. 3.2).

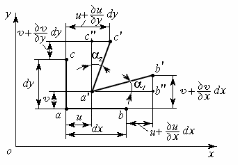
Рис. 3.2

Длина ребра abравнаdx, ребраac - dy. После де­фор­ми­ро­ва­ния точ­киa, bиc займут новые положения -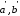и. При этом точкаапо­лу­чит пе­­ремещение, составляющие которого в плоскости чертежаuиv. Точкаb, отстоящая от точкиана бесконечно малом расстоянииdx, по­лу­чит пе­ре­ме­щение, составляющие которого будут отличаться от сос­­тав­ля­ю­щих пе­ре­мещения точкиaна бесконечно ма­лую величину за счет измене­ния ко­ор­динатыx:

.

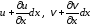Составляющие перемещения точки с будут отличаться от сос­та­в­­­ля­ю­щих перемещения точки a на бесконечно малую величину за счет из­мене­ния координатыy:

.

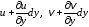Проекция абсолютного удлинения ребра abна осьxпосле де­фор­ма­ции равна:

.

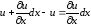Относительное удлинение вдоль оси x, или, по другому, линей­ную де­формацию по направлению осиxзапишем как

.

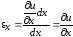Аналогично получим линейные деформации по направлениям ко­­ор­динатных осей yиz:

,.

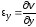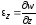Итак, линейная деформация по любому направлению равна ча­с­т­­­­ной производной составляющей перемещения в этом направ­ле­нии по пере­мен­­­ной в том же направлении.

Рассмотрим теперь изменения углов между ребрами парал­ле­ле­пи­пе­да:

.

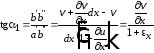Пренебрегая линейной деформацией 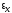по сравнению с едини­цей, по­­­­лучим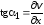и, по аналогии,.

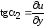Ограничиваясь рассмотрением только малых деформаций, мож­но по­­лагать 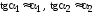, тогда,.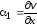

Угол сдвига в плоскости xoy, т. е. искажение прямого углаbac, на­зы­вается угловой деформацией и определяется как сумма углов по­во­рота ре-

бер abиac:.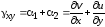

Аналогично найдем угловые деформации в двух других коорди­нат­ных плоскостях:

,.

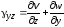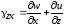Итак, угловая деформация в любой плоскости равна сумме ча­ст­­­ных производных составляющих перемещения в этой плоскости по пе­ре­мен­ным в перпендикулярных направлениях.

Суммируя все вышеизложенное, можно записать шесть основ­ных за­ви­си­мостей составляющих линейных и угловых деформаций от состав­ля­ющих перемещения:

,

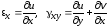(3.1)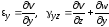

,

.

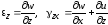Эти уравнения были получены О. Коши (1823 г.) и носят его имя.

В пределе, когда длина ребер параллелепипеда стремится к нулю, фор­­­му­лы (3.1) определяют линейные и угловые деформации в точке a.

Правило знаков для составляющих деформации:

1. Положительным линейным деформациям отвечают удлине­ния по соответствующим направлениям, а отрицательным - укороче­ния.

2. Положительным угловым деформациям соответствует умень­ше­­ние углов между положительными направлениями координатных осей, а от­ри­цательным - увеличение тех же углов.