2.5. Главные напряжения. Главные площадки

Максимальные и минимальные нормальные напряжения (из всех воз­можных на площадках, проходящих через данную точку) на­зы­­­ва­ют­ся главными напряжениями, а площадки, по которым они дей­­­ст­вуют, - глав­ны­ми площадками.

Для определения значений главных напряжений и положения глав­ных площадок необходимо определить экстремум нормального напря­же­ния 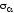, т. е. исследовать функцию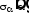на экстремум. А именно вы­чи­с­лить производную поот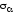и приравнять ее нулю.

Исходя из выражения (2.5) , полу­чим:

,

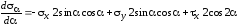или

(2.8)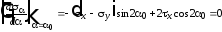

,

где 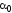- угол нак­ло­­на главных площадок к площадке, в которой дейст­ву­ет напряже­ние.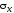

Сравнивая полученное выражение с формулой (2.6) для

,

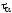
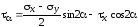можно установить, что

.

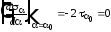Следовательно, по главным площадкам касательные напряже­ния рав­­ны нулю. Поэтому главными площадками можно назвать пло­­­щад­ки, по которым касательные напряжения равны нулю.

Решим уравнение (2.8) относительно угла 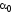, предварительно раз­­­де­лив его на: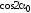

(2.9)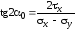

,

или, с учетом закона о парности касательных напряжений, получим:

(2.10)

.

Формулы (2.9), (2.10) выражают значения углов 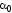, опреде­ля­ю­­­щих по­ложение двух взаимно перпендикулярных площадок. Таким об­ра­зом, глав­­ные площадки взаимно перпендикулярны.

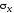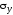Для определения их положения, площадки, в которых дейст­ву­ют нормальные напряжения и, следует повернуть на угол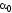против ча­со­вой стрелки (при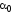> 0) или по часовой стрелке (при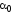< 0).

Отметим, что при любом значени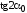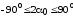и ,или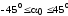, т. е. площадки всегда поворачиваются на угол не боль­ший.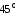

По одной из главных площадок действует максимальное нор­ма­ль­­ное напря­же­ни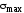е , а по другой - минимальное.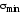

С учетом тригонометрических формул и выражения (2.9), полу­чим:

;

;

;

.

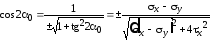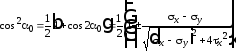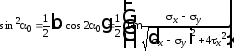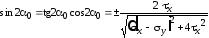Подставив эти выражения в формулу (2.5), после простых пре­об­ра­зо­ваний получим выражения для экстремальных нормальных напря­же­ний:

(2.11)

;

.

Для определения положения главной площадки с напряжением 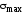необходимо выполнить следующее: площадку с большим (в алге­бра­и­­ческом смысле) нормальным напряжением повернуть на угол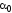(по аб­со­­лютной величине не больший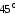) в направлении, в котором вектор ка­са­те­льного напряжения, действующего по этой же площад­ке, стремится вра­щать элементарный параллелепипед отно­си­те­льно его центра.

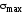После определения положения главной площадки с напряже­ни­ем легко находится перпендикулярная к ней вторая главная пло­щад­ка с напряжением.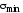

Качественная картина положения главных площадок при раз­лич­­ных исходных напряжениях иприведена на рис. 2.6.

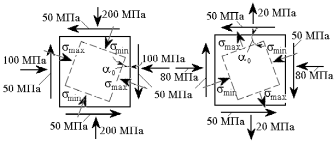
Рис. 2.6

2.6. Экстремальные касательные напряжения. Площадки сдвига

Площадки, по которым касательные напряжения имеют экстре­маль­ные (максимальные и минимальные) значения, называ­ют­ся пло­щад­­­­ками сдвига.

Определим положение этих площадок. Для этого необходимо функ­цию касательных напряжений 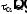исследовать на экстремум, т. е. опре­де­лить ее первую производную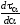

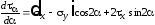
и приравнять полученное выражение нулю:

.

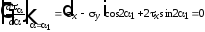Поделив на 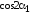, получим

(2.12)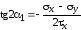

.

Здесь 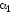- угол наклона площадки сдвига к площадке, по которой дей­­­ствует напряжение.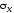

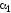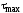Формула (2.12) позволяет вычислить значение угла , опреде­ля­ю­ще­го положение двух вза­им­но перпендикулярных площадок, по одной из ко­то­рых действует мак­симальное касательное напряжение, а по дру­­­гой - мини­мальное.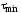

Из закона парности касательных напряжений следует, что 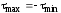. Сравнивая формулу (2.9) с формулой (2.12), легко уста­но­вить, что

,

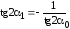откуда

.

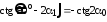
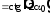Cледовательно, 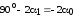, или.

Таким образом, площадка сдвига наклонена к главной пло­щад­­ке под углом, равным .

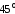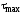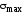Определим величины и. За исходные примем главные нап­ря­женияи.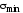

Подставив в формулу (2.6) зна­че­ния 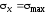,,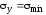, 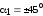получим

,

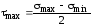(2.13)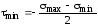

.

Графическая иллюстрация взаимного положения главных площа­док и площадок сдвига представлена на рис. 2.7.

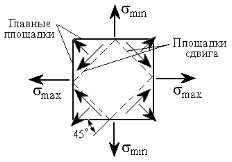
Рис. 2.7

Отметим, что экстремальные касательные напряжения действуют в направ­ле­нии от 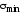к.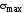

\ РАЗДЕЛ 3. ТЕОРИЯ ДЕФОРМИРОВАННОГО СОСТОЯНИЯ