1.12. Эпюры внутренних сил и моментов.

При расчете на прочность стержневых элементов конструкций необ­хо­димо знать законы изменения внут­рен­них усилий (сил и мо­мен­тов) в поперечных сечениях балки по ее длине. Эти законы мож­но изо­бра­зить с по­мощью специальных гра­фи­ков, называемых эпюра­ми со­от­ветст­ву­ю­щих внутренних силовых факторов.

Например, эпюрой изгибающих моментов (эпюрой M) называ­ет­ся график, изо­бражающий закон изменения величин этих моментов по длине балки. Аналогично эпюрой поперечных сил (эпюройQ) или эпюрой про­доль­ных сил (эпюройN) называется график, изобра­жа­ю­щий изменение по­пе­ре­чных или продольных сил по длине балки.

Каждая ордината эпюры M (илиQ, илиN) представляет собой вели­чи­ну изгибающего момента (или поперечной силы, или про­доль­ной силы) в соответствующем поперечном сечении балки.

1.13. Правила построения эпюр внутренних силовых факторов

Рассмотрим на конкретном примере построение эпюр для балки, на­хо­дящейся под действием системы сил, расположенных в одной пло­с­­­кос­ти (параллельной плоскости чертежа).

Построим эпюры Q иMдля свободно-опертой балки, изобра­жен­ной на рис. 1.8,a, при следующих исходных данных:

; ; ; .

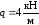Вначале определим опорные реакции. Для этого отбросим опоры и заменим их влияние на балку опорными реакциями и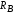(рис. 1.8,б). Реакцииипредставляют собой вертикальную и гори­зон­та­ль­ную составляющие полной реакции шарнирно-непод­виж­ной опо­­рыA; сила жеявляется полной реакцией опорыB. Нап­рав­ле­ние опор­ных реакций выбирается произвольно; если в результате рас­чета зна­че­ние какой-либо реакции получается отрицательным, то, зна­чит, в дей­ст­ви­те­ль­но­­сти ее направление противоположно пред­ва­ри­тель­но при­ня­тому.

Сначала определим опорную реакцию , составив для этого сум­­му проекций всех сил на горизонтальную осьx:

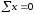;=0.

Очевидно, что не только в рассматриваемом случае, а всегда при дей­­­­ствии на горизонтальную балку только вертикальной нагрузки гори­зон­тальная опорная реакция равна нулю.

Для определения опорной реакции 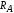составим уравнение мо­мен­тов всех сил относительно точкиB. Опорные реакцииипроходят че­рез эту точку, а потому их моменты относительно нее равны нулю:

;,

где и- равнодействующие погонной равномерно распределенной наг­рузки интенсивностьюqна длинеисоответственно.

,

.

Рис. 1.8

Аналогично составим сумму моментов всех сил относительно то­ч­ки A:

;,

,

.

Для проверки правильности найденных значений опорных реак­ций составим сумму проекций всех сил на ось y:

;,

,

.

Составленное уравнение удовлетворяется тождественно, что ука­зы­­­ва­ет на пра­ви­ль­ность определения опорных реакций.

Для определения аналитических зависимостей дляN,QиMпо дли­не балки выделим на ней участки. Назовем участком балки каждую ее часть, в пределах которой законы изменения поперечной силы и изги­ба­ю­ще­го момента остаются неизменными. Границами участков являются по­пе­реч­ные сечения балки, в которых к ней приложены сос­ре­доточенные нагруз­ки (в том числе и опорные реакции) или в кото­рых начинается ли­бо заканчивается распределенная нагрузка, или в ко­­­торых интен­сив­но­сть этой нагрузки начинает изменяться по новому закону. Текущая коор­ди­на­таxна каждом участке может отсчи­ты­ва­ть­ся как от левого, так и от пра­во­го конца балки. В первом случае при за­писи уравнений равновесия участка необходимо учесть все нагрузки, расположенные левее рассмат­ри­ваемого сечения, а во втором - правее рас­сматриваемого сечения. Вли­я­ние отброшенной части балки на рас­сма­триваемую заменяется внут­рен­ни­ми силамиN,Qи моментомM, направленными в соответст­вии с приня­тым правилом знаков.

Рассматриваемая балка (рис. 1.8) имеет три участ­ка.

Рассмотрим Участок I(рис. 1.9):

,

.

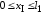Рис. 1.9

(1.1)

.

.

Зависимость для Qна этом участке - линейная, а потому для по­ст­­ро­е­­ния эпю­рыQна этом участке дос­та­то­ч­но опре­де­лить величины по­пе­реч­ной силы при двух значениях: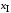

при =0 (на левом конце балки - в на­ча­ле участка I)

== 6,5;

при=(в конце участка I - при отс­че­­те от левого конца балки)

.

,

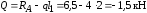(1.2)

.

При =0 (на левом конце балки - в начале участка I)

=0;

при =(в конце участка I- при отсчете от левого конца балки)

.

В формулах (1.1), (1.2) 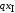- равнодействующая равномерно рас­пре­­­де­ленной нагрузки в пределах отрезка длинойучастка I. Она при­ло­же­на в середине этого отрезка, а потому ее момент относительно рас­смат­ри­ва­е­мого сечения равен (-). Знак изгибающего момента от­рицателен потому, что моментдействует против часовой стрел­­ки.

На первом участке поперечная сила меняет знак с плюса на ми­нус, сле­довательно в каком-то сечении этого участка она равна нулю. Опре­де­лим ко­ординату этого сечения, приравняв нулю выражение для Qв фор­муле (1.1):

.

Теперь, воспользовавшись формулой (1.2) найдем значение из­ги­ба­ю­щего момента в этом сечении балки:

.

Трех точек будет вполне достаточно для построения эпюры M, кото­рая на первом участке изменяется по квадратичному закону.

Орди­на­ты эпюр, соответствующие положительным значениям вну­т­рен­них уси­лий, откладываем вверх от осей этих эпюр, а отри­ца­те­ль­ные - вниз (оси эпюр параллельны оси балки).

Рассмотрим УчастокII(рис. 1.10):

.

.

(1.3)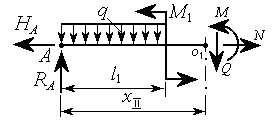

.

.

(1.4)

Рис. 1.10

.

При =(в начале участка II - при отсчете от левого конца бал­ки)

;

при =(в конце участка II - при отсчете от левого конца бал­­­ки)

.

Рассмотрим УчастокIII(рис. 1.11):

.

(1.5)

.

Рис. 1.11

При=0 (на правом конце балки - в на­чале участка III)

;

при =(в конце участка III - при отсчете от правого конца бал­­ки)

.

.

.

(1.6)

При=0 (на правом конце балки - в начале участка III)

;

при =(в конце участка III - при отсчете от правого конца балки)

.

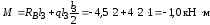На третьем участке поперечная сила меняет знак с плюса на ми­нус, сле­довательно в каком-то сечении этого участка она равна нулю. Оп­ре­де­лим ко­ординату этого сечения, приравняв нулю выражение для Qв формуле (1.5):

.

.

Теперь, воспользовавшись формулой (1.6), найдем значение из­ги­ба­ю­щего момента в этом сечении балки:

.

Анализируя эпюры поперечных сил Q(рис. 1.8,в) и изгибающих мо­ме­н­товM(рис. 1.8,г), мож­но отметить следующие наблюдения.

1. В сечении, в котором к балке приложена сосредоточенная внеш­­­няя сила, перпендикулярная к оси балки (в том числе и опорная реакция в виде сосредоточенной силы), значение поперечной силы Qизменяется скач­кообразно на величину приложенной силы. Когда сос­ре­до­­точенная внешняя сила направлена вверх, на эпюреQ(при переме­ще­нии слева на­право) имеется скачок вверх, а когда сила направлена вниз - ска­чок вниз.

2. В сечении, в котором к балке приложен сосредоточенный внеш­ний момент (в том числе и опорная реакция в виде сос­ре­до­то­чен­но­го мо­ме­н­та), значение изгибающего момента Mизменяется скач­ко­об­разно на величину приложенного момента; когда сосредоточенный внешний мо­мент действует по часовой стрелке, на эпюреM(при пере­ме­щении сле­ва направо) имеется скачок вверх, а когда момент дей­ст­ву­ет против часо­вой стрелки - скачок вниз, т. е. в обоих случаях в сто­ро­ну сжатых волокон.

3. В сечении, в котором поперечная сила Qобращается в нуль, на эпю­ре моментов имеется максимум (если при перемещении слева направо по­перечная сила меняет знак с плюса на минус) или минимум (если при пе­ремещении слева направо поперечная сила меняет знак с минуса на плюс).

Аналитическое обоснование последнего и ряда других наблю­де­ний бу­дет приве­де­но в по­сле­дующих разделах.