
- •Раздел 1. Основные понятия
- •1.1. Общие сведения о сопротивлении материалов
- •1.2. Изучаемые объекты
- •1.3. Расчетные схемы элементов реальных конструкций
- •1.4. Место курса "Сопротивление материалов" в общем цикле дисциплин о механике деформирования упругих тел и образованных из них структур
- •1.5. Нагрузки и их классификация
- •1.6. Внутренние силы
- •1.7. Метод сечений
- •1.8. Основные виды деформаций бруса
- •1.9. Опоры, связи и их классификация
- •1.10. Статически определимые и статически неопределимые балки
- •1.11. Определение реакций в опорных связях
- •1.12. Эпюры внутренних сил и моментов.
- •1.13. Правила построения эпюр внутренних силовых факторов
- •Раздел 2. Теория напряженного состояния
- •2.1. Напряжения
- •2.2. Связь между напряжениями и внутренними усилиями
- •2.3. Виды напряженного состояния
- •2.4. Плоское напряженное состояние
- •2.5. Главные напряжения. Главные площадки
- •2.6. Экстремальные касательные напряжения. Площадки сдвига
- •3.1. Деформации, перемещения
- •3.2. Зависимости между деформациями и перемещениями. Формулы Коши
- •3.3. Основные гипотезы
- •3.4. Кинематические соотношения при изгибе
- •3.5. Экспериментальное изучение механических характеристик материалов при растяжении-сжатии
- •3.6. Испытания материала на растяжение
- •3.7. Определения основных механических характеристик материалов
- •Раздел 5. Уравнения равновесия балки
- •5.1. Уравнения равновесия балки в усилиях
- •5.2. Некоторые особенности эпюр перерезывающих сил и изгибающихмоментов
- •5.3. Уравнения равновесия балки в перемещениях
- •5.4. Ось стержня
- •5.5. Граничные условия
- •5.6. Растяжение и сжатие
- •5.7. Сдвиг. Чистый сдвиг
- •5.8. Деформация при сдвиге. Закон Гука при сдвиге
- •5.9. Кручение
- •Раздел 6. Геометрические характеристики плоских однородных сечений
- •6.1. Cтатический момент инерции сечения
- •6.2. Осевой момент инерции сечения
- •6.5.2. Треугольное сечение
- •6.5.3. Сечение в форме круга
- •6.6. Изменение моментов инерции при параллельном переносе осей
- •6.7. Изменение моментов инерции при повороте осей
- •6.8. Главные моменты инерции. Главные оси инерции
- •6.9. Вычисление моментов инерции сложных сечений
- •Раздел 7. Прямой изгиб
- •7.1. Прямой чистый изгиб
- •7.2. Прямой поперечный изгиб
- •7.3. Формула д.И. Журавского
- •7.4. Расчеты на прочность при изгибе
- •7.5. Балки постоянного поперечного сечения из пластичных материалов
- •7.6. Балки постоянного поперечного сечения из хрупких материалов
- •7.7. Балки переменного поперечного сечения
- •7.8. Определение перемещений в балках постоянного сечения методом непосредственного интегрирования уравнений равновесия
- •7.9. Определение перемещений в балках постоянного сечения методом начальных параметров
- •Раздел 8. Критерии прочности
- •8.1. Основные теории прочности
- •8.1.1. Первая теория прочности, или теория наибольших нормальных напряжений (теория Галилея-Ренкина)
- •8.1.2 Вторая теория прочности, или теория наибольших линейных деформаций (теория Мариотта-Грасгофа, 1862 г.)
- •8.1.3. Третья теория прочности, или теория наибольших касательных напряжений (теория Кулона, 1772 г.)
- •8.1.4. Четвертая (энергетическая) теория прочности, или теория удельной потенциальной энергии формоизменения (Теория Губера-Мизеса-Генки, 1904 г.)
- •8.1.5. Единая теория прочности
- •8.2. Понятия о некоторых новых теориях прочности
- •8.2.1. Критерий прочности Ягна-Бужинского
- •8.2.2. Критерий прочности Писаренко-Лебедева
- •Раздел 9. Сложное сопротивление
- •9.1. Общие положения
- •9.2. Изгиб с кручением брусьев круглого сечения
- •9.3. Эквивалентные напряжения по различным теориям прочности
- •Раздел 10. Расчет конструкций по предельным состояниям
- •10.1. Основные понятия о предельном состоянии
- •10.2. Расчеты при растяжении и сжатии
- •10.3. Расчеты при кручении
- •10.4. Расчеты при изгибе
10.2. Расчеты при растяжении и сжатии

 ,
т. е.
,
т. е.
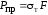 ,
,
Рис. 10.3
Предельно допускаемую нагрузку
определим, разделив
 на коэффициент запаса
на коэффициент запаса :
:
 ,
,
но

и, следовательно,
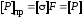 .
.
Таким образом, в рассматриваемом случае предельно допускаемая нагрузка равна допускаемой. Это характерно для расчета любых статически определимых систем, состоящих из центрально растянутых и центрально сжатых стержней.
В статически неопределимых системах
 .
.
10.3. Расчеты при кручении
При кручении прямого бруса в его
поперечных сечениях возникают
только касательные напряжения
 .
Эти напряжения распределены
вдоль радиуса поперечного сечения
по линейному закону (рис. 10.4). Такое
распределение напряжений происходит
лишь в случае, когда величина
.
Эти напряжения распределены
вдоль радиуса поперечного сечения
по линейному закону (рис. 10.4). Такое
распределение напряжений происходит
лишь в случае, когда величина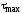 не превышает предела текучести
материала при сдвиге
не превышает предела текучести
материала при сдвиге ,
т. е. когда крутящий момент не
превышает опасной величины для
сплошного сечения
,
т. е. когда крутящий момент не
превышает опасной величины для
сплошного сечения
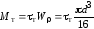 ,
,
(10.2)
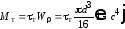
(10.3) - отношение внутреннего диаметра
кольца к наружному. На рис. 10.4 приняты
следующие обозначения:
- отношение внутреннего диаметра
кольца к наружному. На рис. 10.4 приняты
следующие обозначения:
Зона 1 - зона упругого состояния;
Зона 2 - зона пластического состояния;

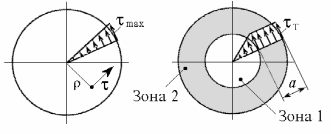
Рис. 10.4
С увеличением крутящего момента ширина
 кольцевой пластической зоны возрастает.
При некотором предельном состоянии
момента
кольцевой пластической зоны возрастает.
При некотором предельном состоянии
момента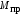 ,
соответствующем полному
исчерпанию несущей способности бруса,
зона упругого состояния материала
исчезает, а зона пластического
состояния материала занимает всю
площадь поперечного сечения. При
этом во всех точках сечения напряжения
равны пределу текучести
,
соответствующем полному
исчерпанию несущей способности бруса,
зона упругого состояния материала
исчезает, а зона пластического
состояния материала занимает всю
площадь поперечного сечения. При
этом во всех точках сечения напряжения
равны пределу текучести .
.
Для определения величины
 выделим в поперечном сечении бруса
элементарную площадкуdF, отстоящую
на расстоянии
выделим в поперечном сечении бруса
элементарную площадкуdF, отстоящую
на расстоянии от его центра. Элементарная
касательная сила, действующая на эту
площадку в предельном состоянии,
равна
от его центра. Элементарная
касательная сила, действующая на эту
площадку в предельном состоянии,
равна а ее момент относительно центра
сечения
а ее момент относительно центра
сечения ,
откуда
,
откуда
(10.4) ,
,
где
 -
пластический полярный момент сопротивления
поперечного сечения.
-
пластический полярный момент сопротивления
поперечного сечения.
Для определения величины пластического
полярного момента сопротивления
выделим в круглом поперечном сечении
кольцо, внутренний радиус которого
 ,
а наружный радиус
,
а наружный радиус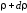 .
.
Пластический полярный момент сопротивления этого кольца
 ,
,
где
 - площадь рассматриваемого кольца.
- площадь рассматриваемого кольца.
Пластический полярный момент сопротивления всего поперечного сечения
 .
.
(10.5) получим выражение
получим выражение
(10.6) .
.
Определим
величину отношения
 :
:

10.4. Расчеты при изгибе
При прямом чистом изгибе бруса в его поперечных сечениях возни-
кают только нормальные напряжения. Рассмотрим эпюры распределения
нормальных
напряжений по высоте сечения (рис. 10.5).
По мере увеличения изгибающего
момента Mнормальные напряжения
возрастают, пока наибольшие их значения
не станут равными пределу текучести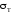 .
При этом изгибающий момент равен
опасному значению
.
При этом изгибающий момент равен
опасному значению .
.
Дальнейшее увеличение изгибающего момента Mприводит к тому,
что напряжения, равные пределу текучести, возникают не только в наиболее удаленных волокнах, но и в некоторой зоне поперечного сечения, которое находится в пластическом состоянии.

Рис. 10.5
При некотором предельном значении
изгибающего момента
 ,
соответствующем полному исчерпанию
несущей способности сечения бруса
на изгиб, упругая зона исчезает, а зона
пластического состояния
занимает всю площадь поперечного
сечения. При этом в сечении образуется
так называемый пластический шарнир
(или шарнир текучести).
,
соответствующем полному исчерпанию
несущей способности сечения бруса
на изгиб, упругая зона исчезает, а зона
пластического состояния
занимает всю площадь поперечного
сечения. При этом в сечении образуется
так называемый пластический шарнир
(или шарнир текучести).
Определим величину предельного
изгибающего момента
 .
Его величина равна моменту всех
элементарных сил
.
Его величина равна моменту всех
элементарных сил и
и относительно нейтральной
оси:
относительно нейтральной
оси:

 .
.
(10.7) называется осевым пластическим моментом
сопротивления и обозначается
называется осевым пластическим моментом
сопротивления и обозначается :
:
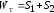 .
.
(10.8)
 .
.
Продольная сила в поперечном сечении при изгибе равна нулю, а потому площадь сжатой зоны сечения равняется площади растянутой зоны. Таким образом, нейтральная ось в сечении, совпадающем с пластическим шарниром, делит это поперечное сечение на две равновеликие части. Следовательно, при несимметричном поперечном сечении нейтральная ось не проходит в предельном состоянии через центр тяжести сечения.
Определим по формуле (10.8) величину
предельного момента
 для стержня прямоугольного сечения
высотойhи ширинойb:
для стержня прямоугольного сечения
высотойhи ширинойb:
 .
.
Опасное значение момента
 равно
равно .
.
Отношение
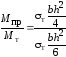 =
1,5. Для круглого сечения отношение
=
1,5. Для круглого сечения отношение
