8.1.1. Первая теория прочности, или теория наибольших нор­ма­ль­ных нап­­ряжений (теория Галилея-Ренкина)

Эта теория предполагает, что прочность сложно­нап­ря­женного эле­ме­­нта будет обеспечена, если наибольшие нормальные напря­же­ния в его се­че­ниях не превышают допускаемого нормального нап­ря­же­ния для ли­ней­но-напряженного элемента из того же материала.

Даже в общем случае напряженного состояния, когда 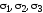не рав­­ны нулю, нужно учитывать только величину наибольшего рас­тя­ги­ва­ю­щего или наибольшего сжимающего напряжения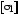, величины же двух дру­гих главных напряжений как будто никакого влияния на проч­ность ма­те­риала не оказывают. Таким образом, получается, что в этой тео­рии нет раз­личия между проверкой прочности при ли­ней­ном и объе­м­ном нап­ря­жен­ных состояниях.

Условие прочности по этой теории выражается неравенством:

(8.2)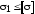

.

Если же у материалов значения допускаемых напряжений на растя­же­­ние и сжатие не равны, т. е. 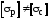, необходимо произ­во­дить про­­ве­рку прочности и на сжатие. Пусть, например,,,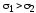, 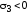тогда условия прочности запишутся так:

(8.3)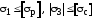

.

Эта теория подтверждается на практике только для весьма хру­п­ких и дос­таточно однородных материалов (стекло, гипс, некоторые ви­ды кера­ми­­ки).

8.1.2 Вторая теория прочности, или теория наибольших линейных дефор­ма­ций (теория Мариотта-Грасгофа, 1862 г.)

Эта теория предполагает, что прочность сложнонапряженного эле­ме­­н­та считается обеспеченной, если наибольшее относительное удлинение не превосходит допускаемого относительного удлинения для линейно- нап­ряженного элемента из того же материала:

(8.4)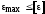

,

где

.

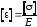(8.5)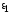

Предположим, что при плоском напряженном состоянии опас­ным от­носительным удлинением будет, т. е.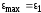. В этом слу­чае, под­ста­вив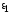в условие (8.4), получим

.

Согласно обобщенному закону Гука,

,

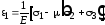поэтому условие прочности (7.5) можно представить в виде

(8.6)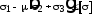

.

Для хрупкого материала условие прочности выражается в виде

(8.7)

.

Вторая теория прочности не подтверждается опытами с плас­тич­­­ны­ми материалами. Она дает удовлетворительный результат при опы­­тах с хру­п­кими материалами, но лишь для некоторых типов нап­ря­женных со­с­то­яний.

8.1.3. Третья теория прочности, или теория наибольших каса­тель­ных нап­ря­­жений (теория Кулона, 1772 г.)

Эта теория предполагает, что прочность сложнонапряженного эле­мен­та обеспечена, если наибольшие касательные напряжения в его се­че­ни­ях не превосходят допускаемого касательного напряжения для линейно - напряженного элемента из этого же материала:

.

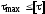Выразив касательные напряжения через главные, условие проч­но­сти по третьей теории можно представить в следующем виде:

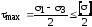
или

(8.8)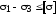

.

Как видно из формулы (8.8), третья теория прочности учи­ты­вает то­ль­ко два главных напряжения из трех - наибольшее и наи­мень­шее. Не­до­статком этой теории является то, что она не прини­ма­ет во внимание про­­межуточного главного напряжения , вли­яю­ще­го на прочность ма­те­ри­ала. Расхождение результатов теоретических рас­четов и опытных дан­ных из-за неучета величины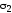достигает 10-15 %.

Третья теория прочности подтверждается результатами опытов для пластичных материалов, одинаково сопротивляющихся растяже­нию и сжа­­тию, а потому ее можно назвать теорией (гипотезой) плас­ти­ч­ности. Она согласуется также и с результатами опытов для все­сто­­роннего сжа­тия. Для хрупких материалов результаты опытов не соот­ветствуют треть­ей теории.