7.9. Определение перемещений в балках постоянного сечения методом начальных параметров

Этот метод впервые упоминается в работах профессора Н.П. Пу­­­зы­­ре­вского и академика А.Н. Крылова. В дальнейшем он по­лу­чил ши­ро­кое при­­­менение при решении разнообразных инже­нер­ных задач.

Рассмотрим балку длиной l, находящуюся в равновесии под дей­ст­вием приложенных к ней внешних сил и опорных реакций. Оп­ре­­делим угол поворота некоторого сечения и его прогиб. Пола­га­ем, что в общей для балки системе координат данное сече­ние нахо­дит­ся на рас­стоянииот левого торца (начала системы коор­ди­нат). На рис. 7.7 показана левая часть балки с положительной вне­ш­­ней наг­руз­кой.

Составим выражения для перерезывающей силы и изгибаю­ще­го момента, возникающих в рассматриваемом поперечном се­че­­нии:

;

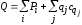(7.22)

.

Рис. 7.7

В выражениях (7.22) каждая величина cозначает расстояние от се­че­ния, в котором приложена соответствующая сосредоточенная на­г­­рузка или начинает действие распределенная нагрузка, до сече­ния, для которого оп­ределяется значениеQи.

Если распределенная нагрузка обрывается в сечении n-n, рас­по­ло­женном левее сечения с абсциссой, то ее следует продолжить до пра­во­го конца балки и одновременно с этим приложить на участ­ке от сеченияn-nдо правого конца балки нагрузку той же величины, но об­рат­но­го зна­ка.

Подставим выражение изгибающего момента по второй из фор­мул (7.22) в дифференциальное уравнение изогнутой оси балки :

.

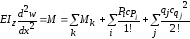Проинтегрируем дважды от 0 до xполученное уравнение, учтя при этом, чтоdx=dc:

;

(7.23)

.

Постоянные интегрирования иотносятся к участкуmбалки. Для их определения рассмотрим два соседних участкаmиm+1 балки, на границе которых приложена сосредото­чен­ная силаP(или при­ложен сосредоточенный моментM, или начи­на­ет­ся действие распре­де­лен­­ной нагрузкиq).

Рис. 6.8

Представим уравнения (7.23) для участкаmэтой балки в виде:

;

,

где ,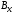- правые части уравнений (7.23) без членов, со­дер­жа­щих пос­то­­­­янные интегрирования.

Для участка m+1 балки уравнения (7.23) примут вид:

;

.

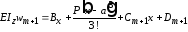На границе участков mиm+1, т. е. приx=а, должно соблюдаться ус­ло­вие неразрывности деформаций (перемещений), которое запишется в ви­де:

и.

Следовательно,

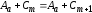
и

,

откуда

и.

Рассматривая аналогично участки m+1 иm+2, получими.

Следовательно,

;

.

Таким образом, постоянные интегрирования C (D), входящие в вы­ра­жения (7.23), одинаковы для всех участков балки от первого до пос­лед­не­го, а потому индексы при этих постоянных в выражениях (7.23) можно опустить. Для определенияCиDсоставим по формулам (7.23) выра­же­ние дляи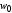(для сечения на левом конце балки, т. е. приx=0). Для этого сечения все расстоянияcравняются нулю. Следовательно,

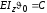и.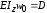

Подставим найденные значения CиDв уравнения (7.23):

;

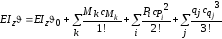(7.24)

.

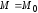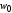Нагрузки и, приложенные к левому концу (на­ча­ль­но­­му сечению) балки, а также перемещенияиэтого конца на­­зы­ва­ю­т­ся начальными параметрами.

По значениям этих параметров, а также нагрузок, приложенных к бал­ке по ее длине, с помощью уравнений (7.24) можно определить углы по­ворота 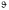и прогибылюбых сечений балки. Поэтому уравнения (7.24) называются уравнениями метода начальных па­ра­мет­ров.

При определении прогибов и углов поворота поперечного се­че­ния бал­­­ки в выражениях (7.24) следует учитывать все приложенные к балке сле­­ва от рассматриваемого сечения внешние сосредо­то­чен­ные и рас­пре­де­лен­­ные нагрузки, включая и опорные реакции.