
- •Раздел 1. Основные понятия
- •1.1. Общие сведения о сопротивлении материалов
- •1.2. Изучаемые объекты
- •1.3. Расчетные схемы элементов реальных конструкций
- •1.4. Место курса "Сопротивление материалов" в общем цикле дисциплин о механике деформирования упругих тел и образованных из них структур
- •1.5. Нагрузки и их классификация
- •1.6. Внутренние силы
- •1.7. Метод сечений
- •1.8. Основные виды деформаций бруса
- •1.9. Опоры, связи и их классификация
- •1.10. Статически определимые и статически неопределимые балки
- •1.11. Определение реакций в опорных связях
- •1.12. Эпюры внутренних сил и моментов.
- •1.13. Правила построения эпюр внутренних силовых факторов
- •Раздел 2. Теория напряженного состояния
- •2.1. Напряжения
- •2.2. Связь между напряжениями и внутренними усилиями
- •2.3. Виды напряженного состояния
- •2.4. Плоское напряженное состояние
- •2.5. Главные напряжения. Главные площадки
- •2.6. Экстремальные касательные напряжения. Площадки сдвига
- •3.1. Деформации, перемещения
- •3.2. Зависимости между деформациями и перемещениями. Формулы Коши
- •3.3. Основные гипотезы
- •3.4. Кинематические соотношения при изгибе
- •3.5. Экспериментальное изучение механических характеристик материалов при растяжении-сжатии
- •3.6. Испытания материала на растяжение
- •3.7. Определения основных механических характеристик материалов
- •Раздел 5. Уравнения равновесия балки
- •5.1. Уравнения равновесия балки в усилиях
- •5.2. Некоторые особенности эпюр перерезывающих сил и изгибающихмоментов
- •5.3. Уравнения равновесия балки в перемещениях
- •5.4. Ось стержня
- •5.5. Граничные условия
- •5.6. Растяжение и сжатие
- •5.7. Сдвиг. Чистый сдвиг
- •5.8. Деформация при сдвиге. Закон Гука при сдвиге
- •5.9. Кручение
- •Раздел 6. Геометрические характеристики плоских однородных сечений
- •6.1. Cтатический момент инерции сечения
- •6.2. Осевой момент инерции сечения
- •6.5.2. Треугольное сечение
- •6.5.3. Сечение в форме круга
- •6.6. Изменение моментов инерции при параллельном переносе осей
- •6.7. Изменение моментов инерции при повороте осей
- •6.8. Главные моменты инерции. Главные оси инерции
- •6.9. Вычисление моментов инерции сложных сечений
- •Раздел 7. Прямой изгиб
- •7.1. Прямой чистый изгиб
- •7.2. Прямой поперечный изгиб
- •7.3. Формула д.И. Журавского
- •7.4. Расчеты на прочность при изгибе
- •7.5. Балки постоянного поперечного сечения из пластичных материалов
- •7.6. Балки постоянного поперечного сечения из хрупких материалов
- •7.7. Балки переменного поперечного сечения
- •7.8. Определение перемещений в балках постоянного сечения методом непосредственного интегрирования уравнений равновесия
- •7.9. Определение перемещений в балках постоянного сечения методом начальных параметров
- •Раздел 8. Критерии прочности
- •8.1. Основные теории прочности
- •8.1.1. Первая теория прочности, или теория наибольших нормальных напряжений (теория Галилея-Ренкина)
- •8.1.2 Вторая теория прочности, или теория наибольших линейных деформаций (теория Мариотта-Грасгофа, 1862 г.)
- •8.1.3. Третья теория прочности, или теория наибольших касательных напряжений (теория Кулона, 1772 г.)
- •8.1.4. Четвертая (энергетическая) теория прочности, или теория удельной потенциальной энергии формоизменения (Теория Губера-Мизеса-Генки, 1904 г.)
- •8.1.5. Единая теория прочности
- •8.2. Понятия о некоторых новых теориях прочности
- •8.2.1. Критерий прочности Ягна-Бужинского
- •8.2.2. Критерий прочности Писаренко-Лебедева
- •Раздел 9. Сложное сопротивление
- •9.1. Общие положения
- •9.2. Изгиб с кручением брусьев круглого сечения
- •9.3. Эквивалентные напряжения по различным теориям прочности
- •Раздел 10. Расчет конструкций по предельным состояниям
- •10.1. Основные понятия о предельном состоянии
- •10.2. Расчеты при растяжении и сжатии
- •10.3. Расчеты при кручении
- •10.4. Расчеты при изгибе
7.5. Балки постоянного поперечного сечения из пластичных материалов
Для таких балок
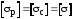 .
В рассматриваемом случае опасным
является то поперечное сечение, в котором
возникает наибольший по абсолютной
величине изгибающий момент
.
В рассматриваемом случае опасным
является то поперечное сечение, в котором
возникает наибольший по абсолютной
величине изгибающий момент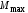 .
Для этого сечения и составляется
условие прочности. Опасными являются
точки поперечного сечения,
наиболее удаленные от нейтральной
оси.
.
Для этого сечения и составляется
условие прочности. Опасными являются
точки поперечного сечения,
наиболее удаленные от нейтральной
оси.
Нормальные напряжения в этих точках определяются по формуле
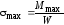 .
.
В результате получим формулу для проверки напряжений
 .
.
(7.13)
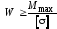 .
.
(7.14) ,
определяемого из выражения
,
определяемого из выражения
(7.15) .
.
Рассмотрим теперь случай, когда расчет балки на прочность только по наибольшим нормальным напряжениям, возникающим в ее опасном поперечном сечении, недостаточен.
Для короткой балки поперечные силы могут иметь значительную величину, в то время как изгибающие моменты могут оказаться сравнительно небольшими. В этих случаях следует проверить максимальные касательные напряжения в том поперечном сечении, в котором поперечная сила имеет наибольшее значение. Эти напряжения не должны превышать допускаемых касательных напряжений, т. е. должно удовлетворяться условие прочности по касательным напряжениям
(7.16) .
.
Для балок обычно принимают
 .
.
7.6. Балки постоянного поперечного сечения из хрупких материалов
К хрупким материалам относится, например, серый литейный чугун. У него предел прочности на растяжение в 3-5 раз меньше предела прочности на сжатие. Поэтому целесообразно, чтобы наибольшие растягивающие напряжения в чугунном брусе были значительно меньше наибольших сжимающих напряжений.
Очевидно, что это требование может быть выполнено для брусьев с поперечным сечением, несимметричным относительно нейтральной оси (рис. 7.5).
Для балки из хрупкого материала составляют два условия прочности:
(7.17)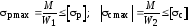 ,
,
где
 .
.
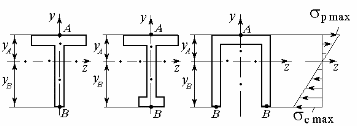
Рис. 7.5
7.7. Балки переменного поперечного сечения
В том случае, когда поперечное сечение балки имеет переменное сечение (жесткость), то те упрощения, которые нам предоставляет универсальное уравнение изогнутой оси, теряются, и следует переходить к прямому интегрированию более сложной функции
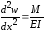 ,
,
где
не только момент, но и жесткость
 являются величинами переменными.
являются величинами переменными.
Интегрирование этой функции может быть осуществлено или аналитически (если это возможно), или численно с использованием одного из известных методов вычислительной математики.
7.8. Определение перемещений в балках постоянного сечения методом непосредственного интегрирования уравнений равновесия
Уравнение изогнутой оси стержня при поперечном изгибе, согласно (6.2) имеет вид
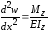 .
.
Проинтегрировав это уравнение один раз, получим уравнение углов поворота сечений балки
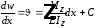 ,
,
где
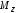 - уравнение эпюры изгибающих моментов
на рассматриваемом участке
балки;С- константа интегрирования.
- уравнение эпюры изгибающих моментов
на рассматриваемом участке
балки;С- константа интегрирования.
Интегрируя второй раз, получим уравнение прогибов (уравнение упругой линии)
(7.19)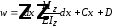 .
.
Для балки постоянного сечения
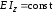 и, следовательно,
и, следовательно,
(7.20)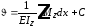 ;
;
(7.21)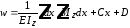 .
.
Постоянные интегрирования CиDопределяются из кинематических граничных условий, т. е. условий, накладываемых на балку при введении опорных связей (рис. 7.6,а,б):
Рис. 7.6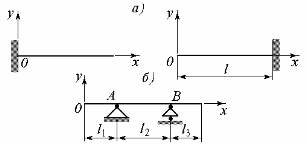
а) консольная балка:
при
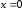 :
: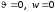 ;
при
;
при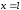 :
: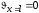 ,
,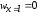 ;
;
б) свободно-опертая балка:
при
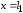 :
: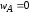 ;
при
;
при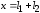 :
: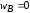 .
.
