6.9. Вычисление моментов инерции сложных сечений

Порядок вычисления моментов инерции сложных сечений при­ве­дем на примере составного сечения, представляющего собой на­бор из трех эле­­ментов: равнополочного уголка, двутавра и пря­мо­угольника. Взаим­ное расположение элементов составного се­че­ния пред­­ставлено на рис. 6.10. Геометрические размеры прямоугольника дол­ж­ны быть за­даны, а дан­­ные по геометрическим харак­те­ри­с­ти­кам для уголка и дву­тавра вы­би­­ра­­ются из соответствующих таблиц сор­та­мента про­кат­ных про­филей.

Для заданного составного сечения:

1. Определяются координаты центров тяжести каждого из эле­мен­тов в общей системе координат :

;;;

;;,

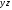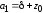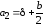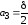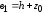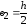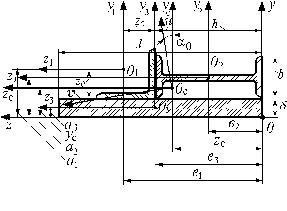
Рис. 6.10

В этих формулах:

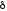- высота прямоугольника;

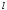- длина прямоугольника;

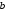- ширина полки двутавра;

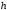- высота профиля двутавра;

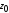- расстояние от центра тяжести уголка до его основания.

В приведенных выше формулах и везде далее верхние и нижние индексы 1, 2, 3 будем относить соответственно к равнополочному уголку, дву­тав­ру и прямоугольнику.

2. Определяется статический момент каждого элемента отно­си­те­ль­но осей yиzобщей системы координат:

;;;

;;,

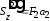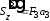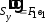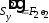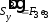где 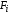(i=1,2,3) - площади соответствующих элементов составного сече­ния.

3. Определяются статические моменты инерции составного сечения от­но­си­тель­но осей общей системы координат 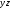как сумма статических мо­­­мен­тов сос­­тав­­ляющих его элементов:

,

.

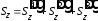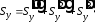4. Определяется положение центра тяжести составного сечения в ко­ор­­динатных осях 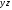по формулам:

,.

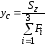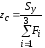5. Определяются осевые моменты инерции составного сечения от­но­­си­­тельно координатных осей 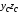, проходящих через центр тяжести сос­тав­­ного сечения:

,

,

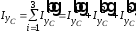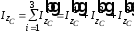где

,,,

,,.

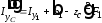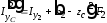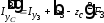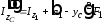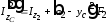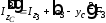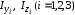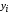В приведенных выше формулах - соответствен­но осе­вые мо­­­­менты инерции равнополочного уголка, двутавра, пря­­мо­у­голь­ни­ка от­но­сительно собственных центральных осейи.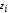

6. Определяется центробежный момент инерции составного сече­ния отно­сительно координатных осей :

,

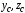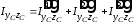где 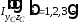центробежные моменты инерции отдельных элемен- тов сложного сечения относительно осей координат: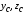

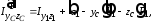
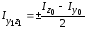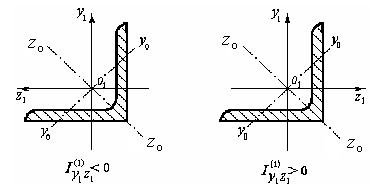
где , а знак плюс (минус) берется в том случае, когда гла­в­ная центральная ось максимум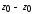равнополочного уголка про­хо­­дит через четные (нечетные) четверти выбранного направления цент­раль­ных осей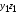(рис. 6.11);

Рис. 6.11

,

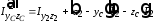где 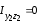, поскольку оси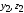для двутавра являются главными ося­ми инер­ции;

,

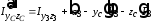где 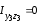, поскольку оси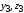для прямоугольника являются глав­ны­ми осями инерции.

7. Определяется положение главных центральных осей инерции сос­та­в­­но­го сечения, согласно формулы (2.32):

.

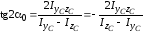При выборе направления главных осей инерции для де­кар­товой пря­­­­моугольной системы координат, кроме правил приведенных выше, мож­­­но руководствоваться и сле­ду­ю­­щи­ми соображениями:

- если , то главная ось, относительно которой момент инер­ции имеет максимальное значение, проходит через I и III квадран­ты (чет­верти);

- если 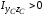, то главная ось, относительно которой момент инер­­­­­­­ции имеет максимальное значение, проходит через II и IV квадран­ты (чет­вер­ти);

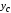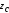- ось максимум всегда составляет меньший угол с той из осей (или), относительно которой осевой момент инерции имеет боль шее значение.

8. Вычислим главные осевые моменты инерции по формулам (2.33):

,

.

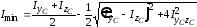Следует отметить, что необходимым условием правильности приве-денного расчета является равенство

.
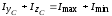