3.7. Определения основных механических характеристик материалов

Введем следующие определения.

1. Пределом пропорциональности называется наибольшее на­пря­жение, до которого деформации изменяются прямо пропор­ци­о­на­льно на­­пряжениям.

2. Пределом упругости называется напряжение, при кото­ром образец получает весьма малую остаточную деформацию (по­ряд­ка 0,001 - 0,005 %) первоначальной длины образца.

3. Пределом текучести называется напряжение, при котором де­формации образца растут без увеличения нагрузки.

4. Пределом прочности 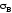называется напряжение, вызванное наи­большей нагрузкой на образец за время эксперимента, от­не­сен­ной к пер­во­начальной площади поперечного сечения образца.

Поскольку на построенной диаграмме ординаты представляют со­бой напряжения, отнесенные к первоначальной площади сечения об­раз­­ца, а не к действительной (уменьшающейся в процессе нагру­же­ния образца), такая диаграмма называется условной. Ею поль­зу­ют­­ся для оп­ределения механических характеристик материала. Диаг­рам­мой ис­тин­ных напря­же­ний, учитывающей действительные по­пе­реч­ные се­че­ния образца на всех этапах его испытания, пользуются в метал­ло­ве­дении при определении ха­рак­теристик пластичности мате­ри­ала.

Особенностью диаграммы растяжения для хрупких материалов (рис. 3.6, a), например чугуна, является то, что вплоть до самого раз­ры­­­ва об­раз­ца наблюдаются незначительные деформации. Разру­ше­ние материала про­­­­­­­­исходит внезапно при очень малых остаточных де­фо­р­мациях. Пло­ща­д­ка текучести отсутствует. Нет строгой про­пор­ци­о­на­ль­ности между нап­ря­жениями и деформациями. Предел проч­нос­ти на раз­рыв у большинства хрупких материалов мал по срав­не­нию с их пре­делом прочности на сжа­тие.

Для таких материалов, как дюралюминий, бронза, высоко­уг­ле­ро­дистые и легированные стали, на диаграмме нет явно вы­ра­жен­ной пло­щад­­ки текучести (рис. 3.6, б). Для таких материалов вводится по­ня­тие ус­лов­­ного предела текучести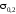- напряжение, соот­вет­ст­ву­ю­щее отно­си­те­ль­­ной остаточной деформации, равной 0,2 %.

а)б)

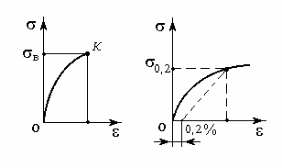
Рис. 3.6

Раздел 5. Уравнения равновесия балки

5.1. Уравнения равновесия балки в усилиях

Выделим из деформированной балки бесконечно малый эле­мент, ко­то­­рый находится в равновесии под действием внешней наг­руз­ки и внут­рен­­них силовых факторов (рис. 5.1).

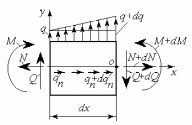
Рис. 5.1

Запишем три уравнения равновесия:

,

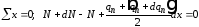или

.

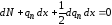Пренебрегая бесконечно малой величиной второго порядка ма­лос­­ти по сравнению с бесконечно малыми первого порядка, оконча­те­ль­но полу­чим

(5.1)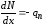

.

.

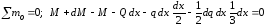Пренебрегая аналогично бесконечно малыми величинами второ­го по­рядка малости в сравнении с малыми первого порядка, по­лу­­чим

(5.2)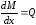

.

;

.

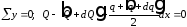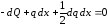Пренебрегая бесконечно малой величиной второго порядка ма­лос­ти по сравнению с малыми первого порядка, полу­чим

(5.3)

.

Уравнения равновесия в усилиях (5.2), (5.3) выражают дифферен­ци­­аль­­­­ные за­ви­симости между изгибающим моментом M, перерезы­ва­ющей си­лойQ и интенсивностью внешней распределенной нагрузкиq.