3.5. Экспериментальное изучение механических характеристик материалов при растяжении-сжатии

Для определения свойств материала при его растяжении и сжа­тии (до­ стадии разрушения) производят механические испытания об­ра­з­цов в лаборатории.

Материалы по их механическим качествам можно разделить на две гру­­­ппы: пластичные и хрупкие. Первые разрушаются только пос­ле значи­те­льной остаточной деформации, хрупкие же - при весьма ма­­лых оста­то­ч­ных деформациях. К пластичным материалам отно­сят­ся: мало­уг­ле­ро­дис­тая сталь, медь, бронза и др.; к хрупким - чугун, бе­тон, ка­мень, кирпич и др.

Один и тот же материал в зависимости от условий, в которых он на­­хо­дится, может вести себя и как пластичный и как хрупкий. Нап­ри­мер, "мягкая сталь" в некоторых случаях сложного сопро­ти­вле­ния, в осо­бен­нос­ти при наличии надрезов, иногда ведет себя как хру­п­кий ма­те­риал. Та же сталь обладает хорошими пластическими свой­с­т­вами при нормальной положительной температуре, а при низкой (от­ри­ца­те­ль­­ной) температуре она приобретает свойства хрупкости. Та­ким обра­зом, было бы правиль­нее говорить о хрупком и пласти­чес­ком состоя­ни­ях материалов.

3.6. Испытания материала на растяжение

Образец стандартной формы закрепляют концами в захваты раз­ры­в­ной машины. Затем образец растягивают постепенно воз­рас­та­ю­щей наг­руз­кой без толчков и ударов. В процессе испытания после­до­ва­тельно от­ме­чают величины нагрузок и измеряют со­от­вет­ст­вующие им удлинения. Испытательные машины обычно снаб­жены специ­аль­ным автоматическим приспособлением, вы­чер­чи­ва­ющим так назы­ва­е­мую диа­­грамму растяже­ния, на которой по оси ординат величины нагру­зок, а по оси абсцисс - ве­ли­чины аб­со­лют­ных удлинений.

Для удобства сравнения результатов испытания нескольких об­ра­з­­цов, имеющих разные размеры, диаграмму растяжения обычно пе­рес­тра­и­­вают в координаты и(рис. 3.5).

В начальный момент, соответствующий началу ко­ор­динат ди­аг­рам­­­мы, =0 и=0. При постепенном уве­ли­чении нагрузки стержень по­­лу­чает удлинение, которое растет прямо пропор­цио­на­ль­­но силе до точкиAдиа­г­­ра­м­мы. ПрямаяOAграфически вы­ражает закон Гу­ка.

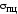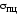На­пряжение, соответствующее крайней точке AпрямойOA, на­зы­ва­ет­ся пределом пропорциональности и обозначается. Для стали мар­­ки Ст. 3=200.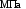

AB- кривая выпуклостью вверх. Прямая пропорциональность меж­дуинарушена и деформации растут быстрее напряжений.

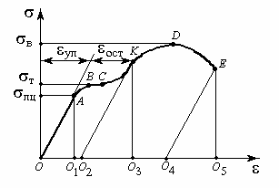
Рис. 3.5

Участок BC- горизонтальная линия - деформации растут даже без уве­­­личения нагрузки, и материал, как говорят, "течет".BC- пло­щад­ка те­ку­чести материала. Напряжение, соответствующее точкеB- пре­дел теку­чес­ти материала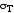. Для стали марки Ст. 3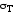=240.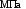

В процессе течения материала на образце появляются едва за­ме­т­­­ные наклонные штрихи под углом около 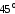к его поперечному се­че­нию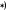(шт­ри­­хи Людерса - Чернова). Появление этих линий можно объ­яснить плас­тическими деформациями, вызванными главным об­ра­­зом касатель­ны­ми напряжениями.

От точки CдоD- пологая кривая. Помимо упругого удлинения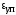об­­­разец получает еще значительное остаточное удлинение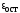. ТочкаD

со­ответствует наибольшему значению нагрузки на образец. Напряжение, соответствующее этой точке, называется пределом про­ч­ности 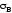мате­ри­а­ла, т. е. наибольшим из возможных для материала на­пряжением, отне­сен­ным к первоначальной площади поперечного се­чения образца. Для стали марки Ст. 3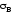=420.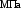

По достижении наибольшей нагрузки деформация, приводящая к разрушению, сосредотачивается в одном месте образца, в резуль­та­те чего появляется сужение его поперечного сечения (шейка), кото­рая становится

___________________________

Строго говоря, как показали теоретические (работа А. Надаи) и экс­пе­ри­­мен­та­ль­ные (работа А.Р. Ржаницына) ис­сле­дования, штрихи Людерса-Чер­­но­ва направлены под углом 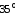к поперечному сечению образца.

все тоньше и тоньше, и, наконец, при напряжении, со­от­­ветствующем точ­ке E, происходит разрыв.

Деформация, выраженная абсциссой 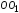, т. е. соответствующая на­пряжению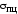является упругой деформацией. Она исчезает после уда­­ле­ния нагрузки.

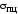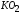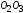Если снять нагрузку с образца за (например, в точкеK), то ли­ния разгрузки изобразится прямой, параллельной прямойOA. В дан­ном случае образец получит кроме упругого удлинения (отрезок) и остаточное удлинение (отрезок).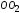

Абсцисса 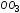представляет собой полное удлинение при напря­же­нии, соответствующем точкеKдиаграммы.

Таким образом, за пределом пропорциональности материала от­носительная деформация .

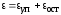Линия 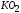диаграммы параллельна линииOA, выражающей за­кон Гука. Следовательно, и за пределом пропорциональности упругие де­фор­ма­ции пропорциональны напряжениям.

Для оценки степени пластичности материала служат величины (в про­­­центах):

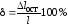- относительное остаточное удлинение при раз­ры­ве (аб­сцисса);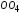

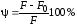- относительное остаточное сужение, где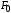- пло­щадь поперечного сечения в месте разрыва (в шейке);- пер­во­на­­чальная пло­щадь поперечного сечения.

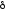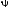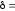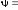Чем больше и, тем более пластичный материал. Для обыч­ных ста­лей8-28 %,30-70 %.

Немного выше, но очень близко к точке Aна диаграмме лежит точ­ка, характеризующая собой предел упругости материала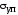. Это нап­ря­же­ние вызывает очень малые остаточные деформации (порядка 0,001 - 0,005 %), которыми можно пренебречь. Поэтому практи­чес­ки считают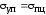.