
- •Краткое содержание
- •Предисловие
- •1. Статус настоящего документа
- •2. Мандат на подготовку настоящего документа
- •3. Значимые нормативно-правовые положения Директивы КПКЗ и определение НДТ
- •4. Цель настоящего документа
- •5. Источники информации
- •6. Как использовать настоящий документ
- •Область применения
- •1. Введение и определения
- •1.1. Введение
- •1.1.1. Энергия в промышленном секторе ЕС
- •1.1.2. Воздействия энергопотребления на окружающую среду и экономику
- •1.1.3. Вклад энергоэффективности в сокращение эффектов глобального потепления и повышение устойчивости
- •1.1.4. Энергоэффективность и Директива КПКЗ
- •1.1.5. Место энергоэффективности в системе комплексного предотвращения и контроля загрязнения
- •1.1.6. Экономические аспекты и вопросы воздействия на различные компоненты окружающей среды
- •1.2. Понятие энергии и законы термодинамики
- •1.2.1. Энергия, теплота, мощность и работа
- •1.2.2. Законы термодинамики
- •1.2.2.1. Первый закон термодинамики: сохранение энергии
- •1.2.2.2. Второй закон термодинамики: рост энтропии
- •1.2.2.3. Баланс эксергии: сочетание первого и второго законов
- •1.2.2.4. Диаграммы свойств
- •1.2.2.5. Дальнейшая информация
- •1.2.2.6. Необратимость и ее источники
- •1.3. Определения показателей энергоэффективности и повышения энергоэффективности
- •1.3.1. Вопросы энергоэффективности и ее оценки в Директиве IPPC
- •1.3.2. Эффективное и неэффективное использование энергии
- •1.3.3 Показатели энергоэффективности
- •1.3.4. Практическое применение показателей
- •1.3.5. Значимость систем и границ систем
- •1.3.6. Другие используемые термины
- •1.3.6.1. Первичная энергия, вторичная энергия и конечная энергия
- •1.3.6.2. Теплота сгорания топлива и КПД
- •1.3.6.3. Меры по повышению энергоэффективности на стороне производителя и стороне потребителя
- •1.4. Показатели энергоэффективности в промышленности
- •1.4.1. Введение: определение показателей и других параметров
- •1.4.2. Энергоэффективность производственных единиц
- •1.4.2.1. Пример 1. Простой случай
- •1.4.2.2. Пример 2. Типичный случай
- •1.4.3. Энергоэффективность предприятия
- •1.5. Вопросы, которые должны быть рассмотрены при определении показателей энергоэффективности
- •1.5.1. Определение границ системы
- •1.5.1.1.Выводы относительно систем и границ систем
- •1.5.2. Другие существенные вопросы, заслуживающие рассмотрения на уровне установки
- •1.5.2.1. Документирование используемых подходов к отчетности
- •1.5.2.2. Внутреннее производство и потребление энергии
- •1.5.2.3. Утилизация энергии отходов и газа, сжигаемого в факелах
- •1.5.2.4. Эффект масштаба (снижение УЭП с ростом объемов производства)
- •1.5.2.5. Изменения в производственных методах и характеристиках продукции
- •1.5.2.6. Интеграция энергосистем
- •1.5.2.7. Неэффективное использование энергии из соображений устойчивого развития и/или повышения энергоэффективности предприятия в целом
- •1.5.2.8. Отопление и охлаждение помещений
- •1.5.2.9. Региональные факторы
- •1.5.2.10. Явная теплота
- •1.5.2.11. Дальнейшие примеры
- •2. Технологии, которые следует рассматривать для обеспечения энергоэффективности на уровне установки
- •2.1. Системы менеджмента энергоэффективности (СМЭЭ)
- •2.2. Планирование и определение целей и задач
- •2.2.1. Постоянное улучшение экологической результативности и вопросы воздействия на различные компоненты окружающей среды
- •2.2.2. Системный подход к менеджменту энергоэффективности
- •2.3. Энергоэффективное проектирование (ЭЭП)
- •2.3.1. Выбор технологии производственного процесса
- •2.4. Повышение степени интеграции процессов
- •2.5. Обеспечение дальнейшего развития инициатив в области энергоэффективности и поддержание мотивации
- •2.6. Поддержание и повышение квалификации персонала
- •2.7. Информационный обмен
- •2.7.1. Диаграммы Сэнки
- •2.8. Эффективный контроль технологических процессов
- •2.8.1. Автоматизированные системы управления технологическими процессами
- •2.8.2. Менеджмент (контроль, обеспечение) качества
- •2.9. Техническое обслуживание
- •2.10. Мониторинг и измерения
- •2.10.1. Косвенные методы мониторинга
- •2.10.2. Оценки и расчеты
- •2.10.3. Учет потребления энергоресурсов и усовершенствованные системы учета
- •2.10.4. Снижение потери давления при измерении расходов в трубопроводах
- •2.11. Энергоаудиты и энергетическая диагностика
- •2.12. Пинч-анализ
- •2.13. Энтальпийный и эксергетический анализ
- •2.14. Термоэкономика
- •2.15. Энергетические модели
- •2.15.1. Энергетические модели, базы данных и балансы
- •2.15.2. Оптимизация использования энергоресурсов и управление ими на основе моделей
- •2.16. Сравнительный анализ
- •2.17. Прочие инструменты
- •3. Технологии, которые следует рассматривать для обеспечения энергоэффективности на уровне энергопотребляющих систем, процессов и видов деятельности
- •3.1. Сжигание
- •3.1.1. Снижение температуры дымовых газов
- •3.1.1.1. Установка подогревателя воздуха или воды
- •3.1.2. Рекуперативные и регенеративные горелки
- •3.1.3. Сокращение массового расхода дымовых газов за счет снижения избытка воздуха горения
- •3.1.4. Автоматизированное управление горелками
- •3.1.5. Выбор топлива
- •3.1.6. Кислородное сжигание
- •3.1.7. Сокращение потерь тепла при помощи теплоизоляции
- •3.1.8. Сокращение потерь тепла через отверстия печей
- •3.2. Паровые системы
- •3.2.1. Общие свойства пара
- •3.2.2. Обзор методов повышения энергоэффективности паровых систем
- •3.2.3. Дросселирование и использование турбодетандеров
- •3.2.4. Методы эксплуатации и управления технологическим процессом
- •3.2.5. Предварительный подогрев питательной воды (в т.ч. с помощью экономайзера)
- •3.2.6. Предотвращение образования и удаление накипи с поверхностей теплообмена
- •3.2.7. Оптимизация продувки котла
- •3.2.8. Оптимизация расхода пара в деаэраторе
- •3.2.9. Оптимизация работы котла короткими циклами
- •3.2.10. Оптимизация парораспределительных систем
- •3.2.11. Теплоизоляция паропроводов и конденсатопроводов
- •3.2.11.1. Использование съемных панелей для теплоизоляции клапанов и фитингов
- •3.2.12. Реализация программы контроля состояния конденсатоотводчиков и их ремонта
- •3.2.13. Сбор и возврат конденсата в котел
- •3.2.14. Использование самоиспарения
- •3.2.15. Утилизация энергии продувочной воды котла
- •3.3. Утилизация тепла и охлаждение
- •3.3.1. Теплообменники
- •3.3.1.1. Мониторинг состояния и техническое обслуживание теплообменников
- •3.3.2. Тепловые насосы (в т.ч. механическая рекомпрессия пара)
- •3.3.3. Системы охлаждения и холодильные установки
- •3.4. Когенерация
- •3.4.1. Различные методы когенерации
- •3.4.2. Тригенерация
- •3.4.3. Централизованное холодоснабжение
- •3.5. Электроснабжение
- •3.5.1. Компенсация реактивной мощности
- •3.5.2. Гармоники
- •3.5.3. Оптимизация систем электроснабжения
- •3.5.4. Энергоэффективная эксплуатация трансформаторов
- •3.6. Подсистемы с электроприводом
- •3.6.1. Энергоэффективные двигатели
- •3.6.2. Выбор оптимальной номинальной мощности двигателя
- •3.6.3. Приводы с переменной скоростью
- •3.6.4. Потери при передаче механической энергии
- •3.6.5. Ремонт двигателей
- •3.6.6. Перемотка
- •3.6.7. Экологические преимущества, воздействие на различные компоненты окружающей среды, применимость и другие соображения относительно методов повышения энергоэффективности систем с электроприводом
- •3.7. Системы сжатого воздуха
- •3.7.1. Оптимизация общего устройства системы
- •3.7.2. Использование приводов с переменной скоростью
- •3.7.3. Высокоэффективные электродвигатели
- •3.7.4. Централизованная система управления системой сжатого воздуха
- •3.7.5. Утилизация тепла
- •3.7.6. Сокращение утечек в системах сжатого воздуха
- •3.7.7. Техническое обслуживание фильтров
- •3.7.8. Использование холодного наружного воздуха для питания компрессоров
- •3.7.9. Оптимизация давления системы
- •3.7.10. Создание запаса сжатого воздуха вблизи потребителей с существенно варьирующим уровнем потребления
- •3.8. Насосные системы
- •3.8.1. Инвентаризация и оценка насосных систем
- •3.8.2. Выбор насоса
- •3.8.3. Оптимизация трубопроводной системы
- •3.8.4. Техническое обслуживание
- •3.8.5. Управление насосными системами и их регулирование
- •3.8.6. Привод и передача
- •3.8.7. Экологические преимущества, воздействие на различные компоненты окружающей среды, применимость и другие соображения относительно методов повышения энергоэффективности насосных систем
- •3.9. Системы отопления, вентиляции и кондиционирования воздуха (ОВКВ)
- •3.9.1. Отопление и охлаждение помещений
- •3.9.2. Вентиляция
- •3.9.2.1. Оптимизация проектных решений при внедрении новой или модернизации существующей системы вентиляции
- •3.9.2.2. Повышение эффективности существующей вентиляционной системы
- •3.9.3. Естественное охлаждение
- •3.10. Освещение
- •3.11. Процессы сушки, сепарации и концентрирования
- •3.11.1. Выбор оптимальной технологии или сочетания технологий
- •3.11.2. Механические процессы
- •3.11.3. Методы термической сушки
- •3.11.3.1. Расчет энергозатрат и КПД
- •3.11.3.2. Конвективная сушка
- •3.11.3.3. Контактная сушка
- •3.11.3.4. Перегретый пар
- •3.11.3.5. Утилизация тепла в процессах сушки
- •3.11.3.6. Выпаривание в сочетании с механической рекомпрессией пара или тепловым насосом
- •3.11.3.7. Оптимизация теплоизоляции сушильных систем
- •3.11.4. Радиационная сушка
- •3.11.5. Системы автоматизированного управления процессами термической сушки
- •4. Наилучшие доступные технологии
- •4.1. Введение
- •4.2. Наилучшие доступные технологии обеспечения энергоэффективности на уровне установки
- •4.2.1. Менеджмент энергоэффективности
- •4.2.2. Планирование и определение целей и задач
- •4.2.2.1. Постоянное улучшение экологической результативности
- •4.2.2.2. Выявление аспектов энергоэффективности установки и возможностей для энергосбережение
- •4.2.2.3. Системный подход к менеджменту энергоэффективности
- •4.2.2.4. Установление и пересмотр целей и показателей в области энергоэффективности
- •4.2.2.5. Сравнительный анализ
- •4.2.3. Энергоэффективное проектирование (ЭЭП)
- •4.2.4. Повышение степени интеграции технологических процессов
- •4.2.5. Поддержание поступательного развития инициатив в области энергоэффективности
- •4.2.6. Поддержание уровня квалификации персонала
- •4.2.7. Эффективный контроль технологических процессов
- •4.2.8. Техническое обслуживание
- •4.2.9. Мониоринг и измерения
- •4.3. Наилучшие доступные технологии обеспечения энергоэффективности энергопотребляющих систем, технологических процессов, видов деятельности и оборудования
- •4.3.1. Сжигание
- •4.3.2. Паровые системы
- •4.3.3. Утилизация тепла
- •4.3.4. Когенерация
- •4.3.5. Электроснабжение
- •4.3.6. Подсистемы с электроприводом
- •4.3.7. Системы сжатого воздуха
- •4.3.8. Насосные системы
- •4.3.9. Системы отопления, вентиляции и кондиционирования воздуха (ОВКВ)
- •4.3.10. Освещение
- •4.3.11. Процессы сушки, сепарации и концентрирования
- •5. Новые технологии обеспечения энергоэффективности
- •5.1. Беспламенное сжигание (беспламенное окисление)
- •5.2. Сжатый воздух как средство хранения энергии
- •6. Заключительные замечания
- •6.1. Временные рамки и основные этапы подготовки настоящего документа
- •6.2. Источники информации
- •6.3. Степень консенсуса
- •6.4. Пробелы и дублирование информации. Рекомендации по дальнейшему сбору информации и исследованиям
- •6.4.1. Пробелы и дублирование информации
- •6.4.3. Конкретная производственная информация
- •6.4.3. Направления дальнейших исследований и практической деятельности
- •6.5. Пересмотр настоящего документа
- •Источники
- •Глоссарий
- •7. Приложения
- •7.1. Энергия и законы термодинамики
- •7.1.1. Общие принципы
- •7.1.1.1. Описание систем и процессов
- •7.1.1.2. Формы энергии и способы ее передачи
- •7.1.2. Первый и второй законы термодинамики
- •7.1.2.1. Первый закон термодинамики: баланс энергии
- •7.1.2.2. Второй закон термодинамики: энтропия
- •7.1.2.2.2. Баланс энтропии для закрытой системы
- •7.1.2.3. Баланс энтропии для открытой системы
- •7.1.2.4. Анализ эксергии
- •7.1.3. Диаграммы свойств, таблицы свойств, базы данных и программы
- •7.1.3.1. Диаграммы свойств
- •7.1.3.2. Таблицы свойств, базы данных и программное моделирование
- •7.1.3.3. Источники неэффективности
- •7.1.4. Использованные обозначения
- •7.1.4.1. Библиография
- •7.2. Примеры термодинамической необратимости
- •7.2.1. Пример 1. Дросселирование
- •7.2.2. Пример 2. Теплообменники
- •7.2.3. Пример 3. Процессы перемешивания
- •7.3. Примеры анализа энергоэффективности производства
- •7.3.1. Производство этилена методом парового крекинга
- •7.3.2. Производство мономера винилацетата (МВА)
- •7.3.3. Горячая прокатка стали
- •7.4. Примеры внедрения систем менеджмента энергоэффективности
- •7.5. Примеры энергоэффективных технологических процессов
- •7.6. Пример подхода к поступательному развитию инициатив в сфере энергоэффективности: «совершенство в производственной деятельности»
- •7.7. Мониторинг и измерения
- •7.7.1. Количественные измерения
- •7.7.2. Оптимизация использования энергоресурсов
- •7.7.3. Энергетические модели, базы данных и балансы
- •7.8. Другие инструменты аудита и поддержки мероприятий по повышению энергоэффективности на уровне предприятия
- •7.8.1. Инструменты аудита и менеджмента энергоэффективности
- •7.9. Сравнительный анализ
- •7.9.1. Нефтеперерабатывающие заводы
- •7.9.2. Австрийское энергетическое агентство
- •7.9.3. Схема для норвежских МСП
- •7.9.4. Соглашения о сравнительном анализе в Нидерландах
- •7.9.5. Сравнительный анализ в стекольной промышленности
- •7.9.6. Распределение энергозатрат и выбросов CO2 между различными видами продукции в сложном последовательном процессе
- •7.10. Примеры к главе 3
- •7.10.1. Паровые системы
- •7.10.2. Утилизация отходящего тепла
- •7.11. Мероприятия на стороне потребителя
- •7.12. Энергосервисные компании
- •7.13. Сайт Европейской комиссии, посвященный вопросам энергоэффективности и Национальные планы действий государств-членов
- •7.14. Европейская схема торговли квотами (ETS)
- •7.15. Оптимизация транспортных систем
- •7.15.1. Энергоаудит транспортных систем
- •7.15.2. Менеджмент энергоэффективности автомобильного транспорта
- •7.15.3. Улучшение упаковки с целью оптимизации использования транспорта
- •7.16. Европейский топливный баланс
- •7.17. Коррекция коэффициента мощности при электроснабжении
1.2.2. Законы термодинамики
Как следует из раздела 1.2.1, энергия может преобразовываться из одной формы в другую при помощи машины или устройства; машины могут также использоваться для совершения работы (см. Приложение 7.1.1).
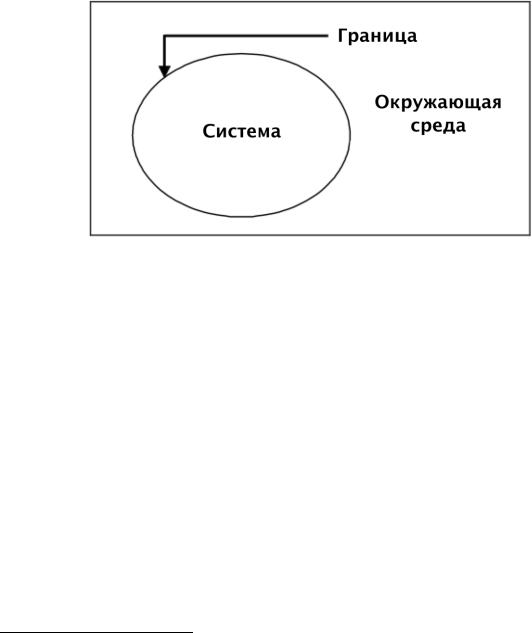
Математические соотношения, описывающие процессы преобразования энергии и выражающие связь соответствующих величин, зависят от того, формулируются ли они для «закрытых» или «открытых» систем. Закрытые системы не обмениваются веществом с окружающей средой, хотя могут взаимодействовать с ней другими способами. Граница такой системы может быть проницаемой для тепла и нежесткой, т.е. за счет изменения объема системы может совершаться работа (см. рис. 1.4).
Реальные промышленные системы являются «открытыми», поскольку они обмениваются веществом с окружающей средой. Для описания системы должны быть определены ее параметры
– например, температура, давление, концентрация веществ, а также скорости изменения этих величин.
Рисунок 1.4: Термодинамическая система
1.2.2.1. Первый закон термодинамики: сохранение энергии
Согласно этому закону, энергия не может ни возникать, ни уничтожаться, и ее количество сохраняется во времени. Возможно только преобразование энергии из одной формы в другую. Это означает, что в стационарном режиме13 общий поток энергии, поступающий в систему с заданными границами, равен общему потоку энергии, покидающей систему.
К сожалению, термины «производство энергии» и «генерация энергии», будучи некорректными в строгом смысле, получили широкое распространение. Они используются и в настоящем документе (это связано с тем, что корректный термин «преобразование энергии» не получил широкого распространения в промышленности и может оказаться непривычным для некоторых читателей). Термин «использование энергии» является корректным, поскольку он не подразумевает ни создания, ни уничтожения энергии. В любом случае, все термины подобного рода, используемые в настоящем документе, означают преобразование энергии из одной формы в другую или совершение работы с использованием энергии (что также связано с преобразованием последней).
Для закрытой системы следствием первого закон термодинамики является тот факт, что изменение полной энергии системы равно поступлению энергии в систему из окружающей среды за счет теплопередачи и совершаемой работы. Это может быть выражено при помощи следующего уравнения:
13 Стационарный режим имеет место, когда состояние и поведение системы, наблюдаемые на протяжении достаточно длительного промежутка времени, не изменяются, например, сила тока или расход вещества в сети остаются постоянными (при неизменных значениях таких физических величин, как напряжение, давление и т.д.).
12

∆U = U2 – U1 = Q – W (в системе СИ все величины в этом уравнении измеряются в джоулях) Где:
U1 – полная энергия системы до изменения;
U2 – полная энергия системы после изменения;
Q – количество теплоты: Q > 0 в том случае, если система получает тепло от окружающей среды; W – работа: W > 0 в том случае, если работа совершается системой.
Теория относительности устанавливает эквивалентность массы и энергии, в результате чего закон сохранения массы оказывается частным случаем закона сохранения энергии. При этом должен иметь место баланс потоков энергии-массы, поступающих в заданную систему и покидающих ее. Поскольку релятивистские эффекты, приводящие к значимому превращению массы покоя в энергию, практически не встречаются в современном промышленном производстве (возможным исключением являются ядерные реакции), возможно составление как энергетических, так и материальных балансов предприятий, производственных систем и процессов. Таким образом, закон сохранения энергии лежит в основе энергетического аудита и деятельности по составлению энергетических балансов (см. раздел 2.11).
В соответствии с первым законом термодинамики, общая эффективность использования энергии или коэффициент полезного действия (в случае тепловой машины, совершающей работу) представляет собой долю подведенного к системе тепла, преобразованную в работу:
η = WQ
где:
η – коэффициент полезного действия; W – работа;
Q – количество теплоты.
Эта же величина может быть выражена в следующей форме: |
|
|
||
КПД η = |
полезная энергия, "произведенная" системой |
= |
работа (W ) |
|
энергия, подведенная к системе |
энергия (E) |
|||
|
|
|||
В системе СИ как полезная работа (W), выполненная системой, так и подведенная к системе энергия измеряются в джоулях, поэтому эффективность (КПД) выражается безразмерной величиной в диапазоне от 0 до 1 или процентной долей. (Примечание: это может не иметь места в ситуации, когда энергия пара, тепловая или электрическая энергия выражается в единицах какого либо специального эквивалента, как, например, в Справочном документе по сжиганию отходов) [254, EIPPCB, 2005, 255, EC, et al., 2005].
1.2.2.2. Второй закон термодинамики: рост энтропии
Второй закон термодинамики утверждает, что энтропия (см. ниже) термодинамически изолированной системы не может уменьшаться с течением времени. Для обратимого процесса и закрытой системы энтропия может быть определена как:
Где:
S – энтропия (единица измерения в СИ – Дж/К);
13

Q – количество теплоты; T – температура.
Этот закон позволяет ввести представление о «качестве» энергии, а также о термодинамической необратимости, определяющей общее направление термодинамических процессов и эволюции вселенной в целом. Строгое математическое понятие энтропии может быть неформально пояснено несколькими способами, иллюстрирующими различные стороны этого понятия:
•более высокая энтропия соответствует большей доле «рассеянной», «бесполезной» или «неизвлекаемой» энергии (представленной хаотическим движением на молекулярном уровне);
•мера частичной потери способности системы к совершению полезной работы вследствие эффектов термодинамической необратимости;
•количественная мера изменения степени беспорядка (например, на молекулярном уровне) между начальным и конечным состоянием системы. Второй закон термодинамики утверждает, что эта величина не может уменьшаться. Одним из следствий этого является тенденция к выравниванию давления или концентрации химических веществ в сообщающихся системах и установлению равновесия в пределах общей системы.
Существуют различные следствия этого закона, некоторые из которых также иллюстрируют понятие роста энтропии14:
•в любом процессе или виде деятельности существует внутренне присущая ему тенденция к потере (или рассеянию) полезной энергии (например, за счет трения), а также к уменьшению способности к совершению полезной работы;
•теплота передается в определенном предсказуемом направлении (например, от горячего тела к холодному);
•невозможно передать тепло от холодной системы к горячей без одновременного преобразования определенного количества энергии в тепловую;
•работа может быть полностью превращена в тепло, но тепло не может быть полностью преобразовано в работу;
•невозможен циклический процесс, единственным результатом которого было бы производство работы за счет тепла, отводимого от единственного резервуара (изолированного источника). Полезная работа может производиться лишь за счет одновременной передачи тепла от горячего к холодному резервуару. Из этого следует невозможность «вечного двигателя второго рода» (работа не может «производиться из ничего»).
На практике это означает, что никакое преобразование энергии не может иметь стопроцентную эффективность с точки зрения получения полезной энергии или работы (см., в частности, обсуждение низшей теплоты сгорания топлива в разделе 1.3.6.2). Однако из этого следует и тот факт, что, уменьшив степень увеличения энтропии в каком-либо процессе, например, в химической реакции, можно повысить энергоэффективность этого процесса.
Таким образом, полная энергия системы может рассматриваться как сумма «полезной» и «бесполезной» энергии.
Мерой содержание тепла в системе является энтальпия (H), называемая также теплосодержанием, которая связана с внутренней энергией (U), давлением (P) и объемом (V):
H = U + PV (размерность энтальпии в системе СИ – джоуль)
U – внутренняя энергия системы, связанная с процессами на уровне микроскопических частиц – атомов и молекул.
14 Существуют и другие следствия этого закона, например, то, что упорядоченность Вселенной неуклонно уменьшается с течением времени.
14
Если система переходит из одного состояния в другое, изменение энтальпии ∆H равно разности энтальпий в начальном и конечном состояниях системы (в случае химической реакции – разности энтальпий продуктов реакции и исходных веществ):
∆H = Hкон – Hнач (в системе СИ размерность всех членов – джоуль)
Общее изменение энтальпии ∆H будет отрицательным, если в процессе изменения система отдает тепло окружающей среде (экзотермический процесс) и положительным, если система получает тепло (эндотермический процесс). Следует заметить, что изменение энтальпии зависит лишь от начального и конечного состояния системы, но не от конкретного процесса. Изменение энтальпии в процессе образования химического соединения из простых веществ называется энтальпией или теплотой образования данного соединения. Энтальпия образования является удельной величиной и представляет собой величину изменения энтальпии на один грамм или моль образующегося соединения. Существуют также стандартные удельные изменения энтальпии для других химических реакций – процессов сгорания, гидрогенизации и т.п.
Изменения фазового состояния вещества также сопровождаются изменением энтальпии, величина которого называется скрытой теплотой или теплотой фазового перехода. Удельная теплота,
связанная с переходом из твердого состояния в жидкое, называется удельной теплотой плавления, а с переходом из жидкого состояния в газообразное – удельной теплотой испарения.
Изменение энергии системы может рассматриваться как состоящее из «полезной» и «бесполезной» компонент, первая их которых может быть использована для совершения полезной работы. Из второго закона термодинамики следует, что для совершения работы необходимо взаимодействие двух систем. Эксергия (B) представляет собой максимальную полезную работу, которая может быть совершена при переходе системы в состояние равновесия с окружающей средой (например, в состояние с той же температурой, давлением, химическим составом, что и среда; см. раздел 1.2.2.4).
Отношение эксергии тела или системы к их полной энергии может рассматриваться как мера качества энергии. Такие формы энергии, как кинетическая и электрическая энергия, а также свободная энергия Гиббса (G) могут быть полностью преобразованы в работу, поэтому их эксергия равна количеству энергии. Однако такие формы энергии, как энергия электромагнитного излучения и тепловая энергия, не могут быть полностью преобразованы в работу, и соответствующая эксергия меньше количества энергии. Конкретное содержание эксергии в веществе или системе определяется соотношением их энтропий в данном состоянии и в равновесии с окружающей средой.
Существует ряд формул для определения эксергии на основе различных параметров системы (температуры, давления, химического состава, энтропии, энтальпии и т.д.). Удельный поток эксергии для материального потока равен:
E = H – H0 – T0(S – S0), где индекс 0 относится к базовым условиям (состоянию среды-приемника)
В качестве практической иллюстрации понятия «полезной энергии» рассмотрим следующий пример. 300 кг пара при температуре 400°C и давлении 40 бар и 6 т воды при 40°C содержат одно и то же количество энергии (по сравнению с одной и той же базовой температурой) – 1 ГДж. Пар при давлении 40 бар способен совершать значительную полезную работу (генерация электроэнергии, приведение в действие механического оборудования и т.д.), однако возможности полезного применения воды с температурой 40°C крайне ограничены. Существуют способы повышения эксергии низкотемпературного пара, однако они требуют затрат энергии из внешнего источника. Так, эксергия может быть повышена при помощи теплового насоса, при работе которого затрачивается энергия.
1.2.2.3. Баланс эксергии: сочетание первого и второго законов
Первый и второй законы термодинамики могут быть объединены в одно уравнение, которое может быть полезным для анализа эксергии, потенциала полезной работы и других характеристик системы. Эта форма законов термодинамики может оказаться полезной для анализа производственных систем, их функционирования и возможностей оптимизации (см. раздел 2.13).
15

Баланс эксергии для открытой системы
Скорость изменения эксергии для открытой системы равна:
где:
Ecv – эксергия при постоянном объеме; T – температура;
t – время;
члены m&iei и m&eee – скорость поступления эксергии в систему и отведения эксергии от системы с входным материальным потоком i и выходным материальным потоком e соответственно ( m&i и m&e представляют собой соответствующие массовые расходы);
Q&j – поток теплоты через границу системы в месте, где мгновенная температура составляет Tj;
I& – скорость «уничтожения» эксергии, мера необратимости; P – давление;
V – объем;
W&cv – работа при постоянном объеме.
Для стационарного режима уравнение баланса приобретает следующий вид:
Применение понятия эксергии в промышленности
Применение понятия эксергии при анализе технологических процессов и проектировании установок в химической промышленности внесло определенный вклад в бурное развитие химической промышленности в XX в. На ранних этапах этого процесса эксергию, как правило, называли «доступной работой».
Одной из целей методов энергетического и эксергетического анализа в процессе проектирования установок является расчет баланса входных и выходных потоков и выбор оптимального проектного решения из нескольких вариантов до строительства установки или реализации технологического процесса. Во многих случаях проектировщик стремится выбрать на основе рассчитанных балансов наиболее эффективный вариант. Однако выбор может не быть самоочевидным, поскольку возможны различные трактовками эффективности (см. раздел 2.13):
•с точки зрения энергетической эффективности, «энергетического КПД» или «КПД по первому закону», наиболее эффективным является процесс, в котором теряется как можно меньшая доля энергии, поступающей в систему;
•с точки зрения эксергетической эффективности, «эксергетического КПД» или «КПД по второму закону», наиболее эффективным является процесс, в котором непроизводительно
16
