7.2.1. Ацп последовательного приближения

АЦП последовательного приближения – это АЦП прямого преобразования со средним быстродействием: число временных тактов одного преобразования равно числу разрядов. Структурная схема такого АЦП изображена на рис. 7.20.

Рис. 7.20. Структурная схема АЦП последовательного приближения

Рассмотрим принцип работы такого АЦП при трехразрядном ЦАП, у которого при опорном напряжении аналоговая «цена» старшего разряда составляет, среднего разряда –и младшего разряда –.

В

Рис. 7.21. Диаграмма напряжений АЦП в процессе уравновешивания методом последовательного приближения

первом такте преобразования схема управления устанавливает код 100, что соответствует напряжению на выходе ЦАП, равному. ЕслиU(n)>, то компаратор устанавливает на выходе 1. Схема управления в следующем такте выставит код 110 и напряжение+. Если это напряжение окажется большеU(n), то по уровню 0 компаратора схема управления убирает 1 из среднего разряда и устанавливает 1 в младший разряд, т. е. код 101. Поскольку последний разряд задействован, то на этом преобразовании заканчивается и код 101, эквивалентный значению U(n), с ошибкой квантования ; записывается в выходной регистр. Аналогичные операции проводятся с каждым дискретным значениемU(n); рис. 7.21.

Потенциальная точность рассмотренного АЦП определяется дискретностью и линейностью ЦАП, а также чувствительностью к смещению нулевого уровня компаратора. Быстродействие ограничивается временем выполнения одного такта, т. е. быстродействием ЦАП и компаратора, и числом разрядов.

7.2.2. Ацп параллельного типа

В таком АЦП анализ уровня выборки сигнала U(n) проводится одновременно по всему диапазону. Это означает, что для n-разрядного кода, когда число квантованных уровней (без учета нулевого) равно 2ⁿ–1, для одновременного анализа потребуется 2ⁿ–1 компараторов, каждый из которых «следит» за своим уровнем, для чего он снабжается соответствующим опорным источником (см. рис. 7.22).

Очевидным преимуществом параллельного АЦП является максимальное быстродействие – преобразование осуществляется за один такт. Очевиден и недостаток – большие аппаратурные затраты. Так, например, для достаточно «грубого» шестиразрядного варианта потребуется 63 компаратора, каждый из которых представляет достаточно сложную микросхему. На практике могут применяться и некоторые комбинированные АЦП, когда, например, два параллельных АЦП оцифровывают m старших разрядов n-разрядного кода. Полученный код формирует на выходе ЦАП «грубое» значение выходного сигнала, разность же между входным и грубым сигналами оцифровывается вторым параллельным АЦП, формирующим n–m младших разрядов.

Рис. 7.22. Структурная схема двухразрядного параллельного ЦАП, состояние для <U(n)<

Основные ограничения потенциальной точности АЦП прямого преобразования определяются параметрами входящих в их структуру ЦАП и шумами входного сигнала, включая и паразитные электромагнитные помехи промышленной частоты.

7.2.3. Ацп интегрирующего типа

В этих преобразователях с помощью интегрирования сигнала и сравнения результата интегрирования с опорным напряжением осуществляется преобразование постоянного напряжения U(n) в пропорциональный временной интервал, длительность которого точно определяется путем подсчета импульсов калиброванной частоты, заполняющих данный отрезок времени. Если время интегрирования выбрать равным периоду сетевой гармонической помехи, интеграл от которой за период равен нулю, то произойдет ее глубокое подавление. Усреднение за этот же период интеграла от более высокочастотных помех также проводит к их практическому исключению. Отсутствие в составе интегрирующего преобразователя ЦАП и подавление шумов позволяет реализовать очень высокую разрядность, не доступную для АЦП прямого преобразования. Естественной платой за это преимущество является снижение быстродействия.

Рассмотрим принцип действия интегрирующих АЦП на примере АЦП двойного интегрирования (рис. 7.23).

а б

Рис. 7.23. АЦП двойного интегрирования:

а – структурная схема; б – диаграммы сигналов на выходе интегратора и генератора

Схема работает в два такта. В первом на вход интегратора на время Т₀ подается измеряемое напряжение U(n) и конденсатор С заряжается до напряжения, равного

,

где ₀ – постоянная интегрирования.

Во втором такте вход интегратора переключается на опорное напряжение , имеющее противоположный входному напряжению знак, – начинается разряд конденсатора

,

где t – длительность разряда. Нуль компаратора фиксирует время T_Х, полагая U_С = 0 t = T_Х – T₀, получим

.

С момента начала второго такта и до момента Т_Х генератор G подает на счетчик последовательность калиброванных по частоте (с известным периодом T_i) импульсов. При известном числе импульсов m легко получить окончательное соотношение

,

в котором все входящие величины имеют высокую стабильность, что обеспечивает высокую точность преобразования. Необходимость задавать значения Т₀, кратное периоду сетевой помехи, делает этот тип АЦП крайне медленным, пригодным для измерения практически только постоянных сигналов.

От этого недостатка свободны АЦП, построенные на принципе сигма-дельта-модуляции, сочетающем высокую точность АЦП двойного интегрирования с существенно большим быстродействием. Структурная схема такого АЦП приведена на рис. 7.24.

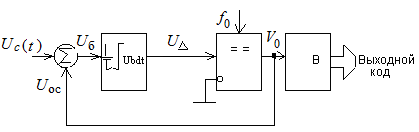
Рис. 7.24. Структурная схема АЦП на принципе сигма-дельта-модуляции

Свое название такой метод получил из-за наличия в структуре суммирующего устройства  (сигма) и нуль-компаратора, определяющего знак приращения сигнала ошибки (дельта). Модулятор, по сути, представляет собой систему с отрицательной обратной связью дискретного типа, поскольку компаратор выдает сигнал только с периодом тактирующих импульсов, следующих с периодом Т₀=1/f₀. Частота дискретизации f₀ выбирается во много раз больше частоты входного сигнала, так, чтобы в течение нескольких десятков периодов Т₀ сигнал мог считаться постоянным. Выходной сигнал компаратора (V₀ при U_>0 и V₀ при U_<0) и является сигналом обратной связи. За счет большого усиления по петле обратной связи (обеспечиваемого компаратором) система стремится рассогласование U_б свести к нулю: U_б = U_С(t) – U_ОС = 0. В процессе выполнения этого условия, происходящего за некоторое число периодов частоты дискретизации, на выходе компаратора генерируется определенная последовательность положительных и отрицательных импульсов. Как будет показано на примерах, анализ этих последовательностей, производимый вычислителем В, позволяет точно определить значение сигнала в некоторый момент времени U_С(t_i) и сформировать соответствующий этому значению код. Рассмотрим несколько примеров, для простоты полагая, что V₀=1 В, а постоянная времени интегратора, выполняющего роль запоминающего устройства, выбрана из условия =Т₀, так, что

.

Пусть значение сигнала за некоторый промежуток времени может считаться неизменным и равным 0,1 В. В табл. 7.1 приведены значения сигналов в характерных точках системы при ее работе.

Таблица 7.1

N такта	U, В	UОС, В	N такта	U, В	UОС, В
1	0,1	+1	12	0,2	+1
2	–0,8	–1	13	–0,7	–1
3	0,3	+1	14	0,4	+1
4	–,6	–1	15	–0,5	–1
5	0,5	+1	16	0,6	+1
6	–0,4	–1	17	–0,3	–1
7	0,7	+1	18	0,8	+1
8	–0,2	–1	19	–0,1	–1
9	0,9	+1	20	1,0	+1
10	0,0	+1	21	0,1	+1
11	–0,9	–1	22	–0,8	–1

Из таблицы видно, что значения сигналов в 1-м и 21-м, 2-м и 22-м тактах повторяются, что свидетельствует о периодичности, генерируемой компаратором последовательности с периодом в 20 тактов. Подсчет значений U_ОС за 20 тактов (например, со 2-го по 21-й), с учетом знаков, дает значение

 U_ОС = +11 + (–9) = 2.

Разделив это число на число тактов за период, получим

.

Для U_С = 0,5 В получим следующие результаты (табл. 7.2).

Таблица 7.2

N такта	U, В	UОС, В
1	0,5	+1
2	0,0	+1
3	–0,5	–1
4	1,0	–1
5	0,5	+1
6	0.0	+1

Теперь периодичность составляет 4 такта, значение

 U_ОС = +3 + (–1) = 2, .

В теории дельта-сигма-модуляции показано, что для диапазона сигнала, укладывающегося в пределы V₀ существует наибольший период, кратный всем возможным периодам при различных значениях сигнала, так что усреднение U_ОС за этот период будет давать точное значение любого сигнала, находящегося в промежутке 0V₀. Таким образом, в дельта-сигма-модуляции происходит усреднение каждой временной выборки сигнала, что резко ослабляет влияние высокочастотных шумов и временные флуктуации параметров схемы. Поэтому рассмотренный принцип обладает в настоящее время максимальными потенциальными метрологическими возможностями. Серийно выпускаются дельта-сигма АЦП, имеющие погрешность от дискретности, соответствующей 24-м двоичным разрядам с нелинейностью 0,0015 %. Естественно, что эта разрядность реализуется для сравнительно низкочастотных сигналов ( 60 Гц). С повышением частоты разрядность резко снижается и для частоты  1 кГц составляет всего 12 разрядов.