- •«Национальный исследовательский
- •I. Основы АнАлоговой электроники
- •1. Задачи, решаемые электронной техникой, и элементы, необходимые для их решения
- •1.1. Электрические сигналы. Временное и спектральное представление
- •1.2. Усиление электрических сигналов
- •1.3. Модуляция сигналов
- •1.3.1. Амплитудная модуляция
- •1.3.2. Импульсно-кодовая модуляция
- •1.3.3. Широтно-импульсная модуляция
- •А б Рис. 1.19. Компаратор: а – схема; б – временные диаграммы при шим1.4. Фильтрация сигналов
- •1.5. Хранение и отображение информации
- •1.6. Преобразование электрической энергии
- •Контрольные вопросы и задания
- •Основные результаты первой главы
- •2. Математический аппарат описания электронных элементов
- •2.1. Описание нелинейных элементов
- •2.2. Линеаризация нелинейных уравнений
- •2.3. Частотный анализ линеаризованных цепей
- •2.4. Временной анализ линеаризованных цепей
- •Контрольные вопросы и задания
- •Основные результаты второй главы
- •3. Полупроводники – основа современной элементной базы электроники
- •3.1. Преимущества полупроводниковых элементов перед электровакуумными
- •3.2. Физические основы электропроводности полупроводников
- •3.3. Электропроводность беспримесного (собственного) полупроводника
- •3.4. Электропроводность примесных полупроводников
- •3.4.1. Донорная примесь
- •3.4.2. Акцепторная примесь
- •3.6. Инерционностьp-n-перехода
- •3.6.1. Зарядная емкостьp-n-перехода
- •3.6.2. Диффузионная емкость
- •3.7. Пробой p-n-перехода
- •3.7.1. Тепловой пробой
- •3.7.2. Электрический пробой
- •3.8. Математическая модельp-n-перехода
- •3.9. Переходметалл – полупроводник
- •Контрольные вопросы и задания
- •Основные результаты третьей главы
- •4. Многопереходные электронные элементы
- •4.1. Полупроводниковые триоды (биполярные транзисторы)
- •4.2. Активный режим работы биполярного транзистора
- •4.3. Статические характеристики биполярного транзистора для активного режима
- •4.4. Инерционность биполярного транзистора
- •4.5. Пробой коллекторного перехода
- •4.7. Нелинейная модель биполярного транзистора
- •4.8. Линеаризованная модель биполярного транзистора
- •4.9. Ключевой режим биполярного транзистора
- •4.10. Полевые транзисторы
- •4.11. Полевые транзисторы с управляющимp-n-переходом
- •4.12. Полевые транзисторы с изолированным затвором
- •4.13. Ключевой режим работы полевых транзисторов
- •4.14. Тиристоры
- •4.15. Элементы оптоэлектроники
- •4.15.1. Управляемые источники излучения
- •4.15.2. Фотоприемники
- •Контрольные вопросы и задания
- •Основные результаты четвертой главы
- •5. Основы теории электронных усилителей
- •5.1. Общие положения
- •Контрольные вопросы и задания
- •5.2. Обратная связь в усилительных устройствах
- •5.2.1. Влияние обратной связи на коэффициент усиления.
- •5.2.2. Влияние обратной связи на нестабильность усилителя
- •5.2.3. Влияние обратной связи на нелинейные искажения и шумы усилителя
- •5.2.4. Влияние обратной связи на входное и выходное сопротивления усилителя
- •5.2.5. Устойчивость усилителей с обратной связью
- •5.2.6. Коррекция частотных характеристик для обеспечения устойчивости усилителя
- •Контрольные вопросы и задания
- •5.3. Принципы построения усилительных каскадов
- •5.3.1. Цепи задания и стабилизации режима покоя
- •5.3.2. Элементы связи усилительных устройств
- •К Рис. 5.34. Оптическая связь онтрольные вопросы и задания
- •5.4. Операционные усилители
- •5.4.1. Модели оу
- •5.4.2. Масштабирующий инвертирующий усилитель
- •5.4.3. Масштабирующий неинвертирующий усилитель
- •5.4.4. Суммирующий усилитель
- •5.4.5. Вычитающий усилитель
- •5.4.6. Интегрирующий усилитель
- •5.4.7. Нелинейные функциональные преобразователи сигналов
- •Контрольные вопросы и задания
- •5.5. Усилители мощности
- •5.5.1. Линейные усилители мощности
- •5.5.2. Усилители мощности ключевого типа
- •Контрольные вопросы и задания
- •Основные результаты пятой главы
- •6. Автогенераторы
- •Основные результаты шестой главы
- •7. Источники вторичного электропитания электронных устройств
- •7.1. Классическая схема вторичного источника (без преобразования частоты сети)
- •7.2. Функциональные элементы вторичных источников электропитания
- •7.2.1. Преобразователи переменного напряжения
- •7.2.2. Стабилизаторы постоянного напряжения
- •7.3. Вторичные источники с преобразованием частоты сети
- •Vd Схема упр.
- •Vd Схема упр. Ul
- •Контрольные вопросы и задания
- •Основные результаты седьмой главы
- •II. Основы цифровой электроники
- •1. Введение
- •2. Логические функции
- •2.1. Логические функции и способы их представления
- •2.2. Основы алгебры логики
- •2.2.1. Функция не
- •2.2.2. Функция или
- •2.2.3. Функция и
- •2.3. Логические элементы и-не, или-не
- •2.3.1. Элемент и-не (штрих Шеффера)
- •2.3.2. Элемент или-не (стрелка Пирса)
- •2.4. Синтез логических устройств
- •2.5. Выбор системы логических элементов
- •2.6. Минимизация логических функций
- •Контрольные вопросы и задания
- •3. Характеристики и параметры логических элементов, основы схемотехники
- •3.1. Логические уровни, нагрузочная способность
- •3.2. Логические элементы с тремя состояниями
- •3.3. Быстродействие логических элементов
- •3.4. Помехоустойчивость логических элементов
- •3.5. Число входов логических элементов
- •3.6. Специальные типы логических элементов. Логические элементы с открытым коллектором
- •3.6.1. Расширители числа входов
- •3.6.2. Схема согласования уровней
- •3.6.3. Логический элемент с разрешением по входу
- •Контрольные вопросы и задания
- •4. Цифровые устройства комбинационного типа
- •4.1. Преобразователи кодов, шифраторы, дешифраторы
- •4.2. Мультиплексоры
- •4.3. Сумматоры
- •4.4. Цифровые компараторы
- •Контрольные вопросы и задания
- •5. Последовательностные цифровые устройства
- •5.1. Триггеры
- •5.1.5. Триггер Шмитта
- •5.2. Цифровые счетчики импульсов и делители частоты следования
- •5.2.1. Двоичные счетчики
- •5.2.2. Недвоичные счетчики
- •5.3. Регистры
- •Контрольные вопросы и задания
- •6. Генераторы импульСныхСигналов
- •6.1. Автогенераторы прямоугольных импульсов (мультивибраторы)
- •6.2. Ждущий (заторможенный) режим генераторов
- •6.3. Интегральные таймеры
- •6.4. Генераторы линейно изменяющегося напряжения (тока)
- •Контрольные вопросы и задания
- •7. УстройствасОпРяжЕнияцифровых и аналоговых систем
- •7.1. Цифроаналоговые преобразователи
- •7.2. Аналого-цифровые преобразователи
- •7.2.1. Ацп последовательного приближения
- •7.2.2. Ацп параллельного типа
- •7.2.3. Ацп интегрирующего типа
- •Контрольные вопросы и задания
- •8. Введение в микропроцессорную технику
- •8.1. Арифметическо-логические устройства
- •8.2. Полупроводниковые запоминающие устройства
- •8.3. Программируемые логические интегральные матрицы
- •8.4. Интерфейсные устройства
- •Контрольные вопросы и задания
- •Приложение справочные данные интегральных схем
- •Литература
- •Оглавление
4.3. Сумматоры
Сумматором называется комбинационная схема, предназначенная для сложения двоичных чисел. Простейшая задача – сложение двух одноразрядных чисел. Для того чтобы разработать логическую схему, в первую очередь следует рассмотреть все возможные сочетания входных переменных, на основании чего можно составить таблицу состояний. При сложении одноразрядных чисел A и B могут наблюдаться следующие комбинации:
|
0 |
+ |
0 |
= |
0; |
|
0 |
+ |
1 |
= |
1; |
|
1 |
+ |
0 |
= |
1; |
|
1 |
+ |
1 |
= |
10, |
Таблица 4.8
|
a0 |
b0 |
S0 |
P |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
. е. еслиA=B=1, происходит перенос в следующий (более старший) разряд. Следовательно, такой сумматор должен иметь два выхода: один для формирования части суммы, относящейся к данному разряду, и второй – для переноса в следующий разряд. Представляя числа
Отсюда составляем логические уравнения в СДНФ:
1)
![]() ;
;
2) P = a0 b0
и строим структурные схемы (рис. 4.14, рис. 4.15).

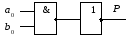
Рис. 4.14. Сумматор по модулю два Рис. 4.15. Схема переноса
Схема, реализующая уравнение 1, называется исключающее ИЛИ, выпускается в сериях как отдельная микросхема. Графическое обозначение приведено на рис 4.16. Логическая операция, выполняемая этой схемой, –
![]() ,
,
где
![]() –
символ суммирования по модулю два.
–
символ суммирования по модулю два.
Е
Рис. 4.16. Исключающее
ИЛИ
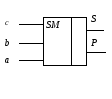
Рис.
4.17. Полусумматор
А
B
Q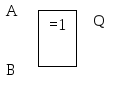

Е
S
P
b![]()
Соединяя полусумматоры и полные сумматоры, получают устройства для сложения многоразрядных чисел.
HS
|
|
|
а б
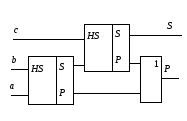
Рис. 4.18. Полный сумматор:
а – структурная схема; б – условное обозначение
4.4. Цифровые компараторы
Устройства, предназначенные для сравнения двух чисел (A и B), представленных в двоичной форме: a1, a2, …, am и b1, b2, …, bm. Результатом сравнения является обнаружение одного из трех возможных состояний: A = B, A > B или A < B.
Таблица состояний одноразрядного компаратора (табл. 4.9).
|
Таблица 4.9 | ||||
|
a |
b |
ya>b |
ya=b |
ya<b |
|
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
|
1 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
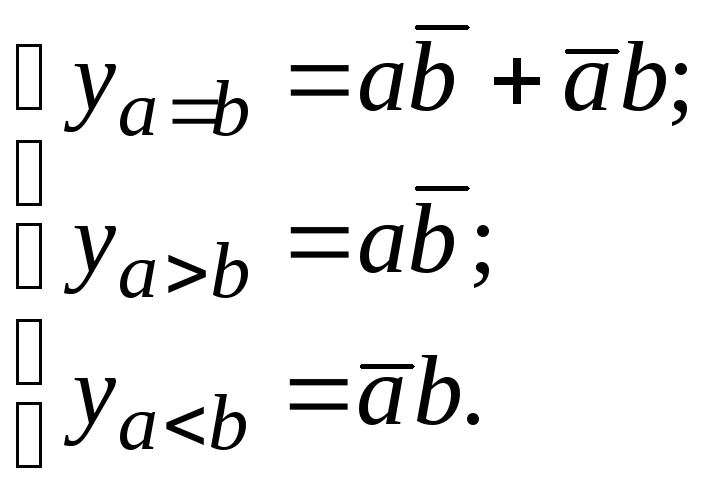
Соответственно структурная схема одноразрядного компаратора рис. 4.19.

Рис. 4.19. Структура одноразрядного компаратора
Для сравнения многоразрядных двоичных чисел используется следующий алгоритм. Сначала сравниваются значения старших разрядов. Если они различны, то эти разряды и определяют результат сравнения. Если они равны, то необходимо сравнивать следующие за ними, более младшие, разряды. Условное изображение цифрового компаратора приведено на рис. 4.20. Входы (A = B, A > B, A < B) служат для наращивания разрядности компаратора (каскадное соединение).

Рис. 4.20. Условное изображение цифрового компаратора