2. Логические функции

2.1. Логические функции и способы их представления

Обработка информации, представленной цифровыми сигналами, сводится к реализации функциональных зависимостей

,

в которых как значение y, так и значение аргументовx_iмогут принимать только значения логического нуля или логической единицы. Такие функции называютсялогическими(переключательными). Теория таких функций развита в специальном разделе математики – теории переключательных функций (булевой алгебры). Логические функции могут быть описаны словесно, в виде алгебраических выражений, таблиц (истинности), специальных карт (карт Карно) и т. д.

Н

N	x3	x2	x1	y
0	0	0	0
1	0	0	1
2	0	1	0
3	0	1	1
4	1	0	0
5	1	0	1
6	1	1	0
7	1	1	1

Рис. 2.1. Общая часть таблицы истинности для логической функции трех аргументов

а рис. 2.1 приведена часть таблицы истинности для трех аргументов, которая имеет одинаковый вид для любой функции. Конкретизация логической функции достигается заполнением графыу.

Таблица имеет число строк, равное n = 2ⁿ, гдеn– число аргументов. Каждое сочетание значений аргументов, называемое набором, нумеруется десятичными числами (включая нуль). Справа от номера набора записывается двоичный код, соответствующий десятичному номеру набора. При этом предполагается, что в графех₁записывается значение младшего разряда двоичного кода (2⁰), в графех₂– значение следующего двоичного кода (2¹) и т. д. Тем самым упорядочивается запись и гарантируется учет всех возможных сочетаний аргументов. Другие способы задания переключательных функций будут рассмотрены позже.

2.2. Основы алгебры логики

В теории переключательных функций доказано, что любую логическую функцию можно реализовать с помощью лишь трех элементарных логических функций:

• логического отрицания (инверсии) – функции НЕ;

• логического сложения (дизъюнкции) – функции ИЛИ;

• логического умножения (конъюнкции) – функции И.

Аппаратно эти функции реализуются в виде цифровых схем – логических элементов. Ниже приведены словесные описания, таблицы истинности, алгебраическая форма записи элементарных функций и условные графические изображения соответствующих логических элементов (для простоты приведены функции ИЛИ, И двух аргументов, хотя реально число аргументов может быть и больше).

2.2.1. Функция не

Алгебраическая форма:
Словесное описание:	«Y есть не Х»
Таблица истинности:
Условное графическое изображение:

Аппаратно элемент НЕ реализуется в виде инвертора – усилительного каскада, работающего в ключевом режиме (рис. 2.2).

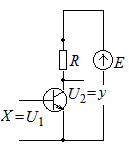
а б в

Рис. 2.2. Схема простейшего инвертора (а); состояние высокого выходного уровня (б); состояние низкого выходного уровня (в)