
- •«Национальный исследовательский
- •I. Основы АнАлоговой электроники
- •1. Задачи, решаемые электронной техникой, и элементы, необходимые для их решения
- •1.1. Электрические сигналы. Временное и спектральное представление
- •1.2. Усиление электрических сигналов
- •1.3. Модуляция сигналов
- •1.3.1. Амплитудная модуляция
- •1.3.2. Импульсно-кодовая модуляция
- •1.3.3. Широтно-импульсная модуляция
- •А б Рис. 1.19. Компаратор: а – схема; б – временные диаграммы при шим1.4. Фильтрация сигналов
- •1.5. Хранение и отображение информации
- •1.6. Преобразование электрической энергии
- •Контрольные вопросы и задания
- •Основные результаты первой главы
- •2. Математический аппарат описания электронных элементов
- •2.1. Описание нелинейных элементов
- •2.2. Линеаризация нелинейных уравнений
- •2.3. Частотный анализ линеаризованных цепей
- •2.4. Временной анализ линеаризованных цепей
- •Контрольные вопросы и задания
- •Основные результаты второй главы
- •3. Полупроводники – основа современной элементной базы электроники
- •3.1. Преимущества полупроводниковых элементов перед электровакуумными
- •3.2. Физические основы электропроводности полупроводников
- •3.3. Электропроводность беспримесного (собственного) полупроводника
- •3.4. Электропроводность примесных полупроводников
- •3.4.1. Донорная примесь
- •3.4.2. Акцепторная примесь
- •3.6. Инерционностьp-n-перехода
- •3.6.1. Зарядная емкостьp-n-перехода
- •3.6.2. Диффузионная емкость
- •3.7. Пробой p-n-перехода
- •3.7.1. Тепловой пробой
- •3.7.2. Электрический пробой
- •3.8. Математическая модельp-n-перехода
- •3.9. Переходметалл – полупроводник
- •Контрольные вопросы и задания
- •Основные результаты третьей главы
- •4. Многопереходные электронные элементы
- •4.1. Полупроводниковые триоды (биполярные транзисторы)
- •4.2. Активный режим работы биполярного транзистора
- •4.3. Статические характеристики биполярного транзистора для активного режима
- •4.4. Инерционность биполярного транзистора
- •4.5. Пробой коллекторного перехода
- •4.7. Нелинейная модель биполярного транзистора
- •4.8. Линеаризованная модель биполярного транзистора
- •4.9. Ключевой режим биполярного транзистора
- •4.10. Полевые транзисторы
- •4.11. Полевые транзисторы с управляющимp-n-переходом
- •4.12. Полевые транзисторы с изолированным затвором
- •4.13. Ключевой режим работы полевых транзисторов
- •4.14. Тиристоры
- •4.15. Элементы оптоэлектроники
- •4.15.1. Управляемые источники излучения
- •4.15.2. Фотоприемники
- •Контрольные вопросы и задания
- •Основные результаты четвертой главы
- •5. Основы теории электронных усилителей
- •5.1. Общие положения
- •Контрольные вопросы и задания
- •5.2. Обратная связь в усилительных устройствах
- •5.2.1. Влияние обратной связи на коэффициент усиления.
- •5.2.2. Влияние обратной связи на нестабильность усилителя
- •5.2.3. Влияние обратной связи на нелинейные искажения и шумы усилителя
- •5.2.4. Влияние обратной связи на входное и выходное сопротивления усилителя
- •5.2.5. Устойчивость усилителей с обратной связью
- •5.2.6. Коррекция частотных характеристик для обеспечения устойчивости усилителя
- •Контрольные вопросы и задания
- •5.3. Принципы построения усилительных каскадов
- •5.3.1. Цепи задания и стабилизации режима покоя
- •5.3.2. Элементы связи усилительных устройств
- •К Рис. 5.34. Оптическая связь онтрольные вопросы и задания
- •5.4. Операционные усилители
- •5.4.1. Модели оу
- •5.4.2. Масштабирующий инвертирующий усилитель
- •5.4.3. Масштабирующий неинвертирующий усилитель
- •5.4.4. Суммирующий усилитель
- •5.4.5. Вычитающий усилитель
- •5.4.6. Интегрирующий усилитель
- •5.4.7. Нелинейные функциональные преобразователи сигналов
- •Контрольные вопросы и задания
- •5.5. Усилители мощности
- •5.5.1. Линейные усилители мощности
- •5.5.2. Усилители мощности ключевого типа
- •Контрольные вопросы и задания
- •Основные результаты пятой главы
- •6. Автогенераторы
- •Основные результаты шестой главы
- •7. Источники вторичного электропитания электронных устройств
- •7.1. Классическая схема вторичного источника (без преобразования частоты сети)
- •7.2. Функциональные элементы вторичных источников электропитания
- •7.2.1. Преобразователи переменного напряжения
- •7.2.2. Стабилизаторы постоянного напряжения
- •7.3. Вторичные источники с преобразованием частоты сети
- •Vd Схема упр.
- •Vd Схема упр. Ul
- •Контрольные вопросы и задания
- •Основные результаты седьмой главы
- •II. Основы цифровой электроники
- •1. Введение
- •2. Логические функции
- •2.1. Логические функции и способы их представления
- •2.2. Основы алгебры логики
- •2.2.1. Функция не
- •2.2.2. Функция или
- •2.2.3. Функция и
- •2.3. Логические элементы и-не, или-не
- •2.3.1. Элемент и-не (штрих Шеффера)
- •2.3.2. Элемент или-не (стрелка Пирса)
- •2.4. Синтез логических устройств
- •2.5. Выбор системы логических элементов
- •2.6. Минимизация логических функций
- •Контрольные вопросы и задания
- •3. Характеристики и параметры логических элементов, основы схемотехники
- •3.1. Логические уровни, нагрузочная способность
- •3.2. Логические элементы с тремя состояниями
- •3.3. Быстродействие логических элементов
- •3.4. Помехоустойчивость логических элементов
- •3.5. Число входов логических элементов
- •3.6. Специальные типы логических элементов. Логические элементы с открытым коллектором
- •3.6.1. Расширители числа входов
- •3.6.2. Схема согласования уровней
- •3.6.3. Логический элемент с разрешением по входу
- •Контрольные вопросы и задания
- •4. Цифровые устройства комбинационного типа
- •4.1. Преобразователи кодов, шифраторы, дешифраторы
- •4.2. Мультиплексоры
- •4.3. Сумматоры
- •4.4. Цифровые компараторы
- •Контрольные вопросы и задания
- •5. Последовательностные цифровые устройства
- •5.1. Триггеры
- •5.1.5. Триггер Шмитта
- •5.2. Цифровые счетчики импульсов и делители частоты следования
- •5.2.1. Двоичные счетчики
- •5.2.2. Недвоичные счетчики
- •5.3. Регистры
- •Контрольные вопросы и задания
- •6. Генераторы импульСныхСигналов
- •6.1. Автогенераторы прямоугольных импульсов (мультивибраторы)
- •6.2. Ждущий (заторможенный) режим генераторов
- •6.3. Интегральные таймеры
- •6.4. Генераторы линейно изменяющегося напряжения (тока)
- •Контрольные вопросы и задания
- •7. УстройствасОпРяжЕнияцифровых и аналоговых систем
- •7.1. Цифроаналоговые преобразователи
- •7.2. Аналого-цифровые преобразователи
- •7.2.1. Ацп последовательного приближения
- •7.2.2. Ацп параллельного типа
- •7.2.3. Ацп интегрирующего типа
- •Контрольные вопросы и задания
- •8. Введение в микропроцессорную технику
- •8.1. Арифметическо-логические устройства
- •8.2. Полупроводниковые запоминающие устройства
- •8.3. Программируемые логические интегральные матрицы
- •8.4. Интерфейсные устройства
- •Контрольные вопросы и задания
- •Приложение справочные данные интегральных схем
- •Литература
- •Оглавление
2.3. Частотный анализ линеаризованных цепей
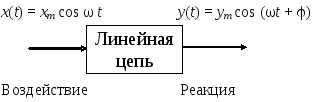
При частотном анализе определяется установившееся значение реакции цепи на гармоническое воздействие
x(t)=xm sin t.
Хотя реальные сигналы, действующие в электронных цепях, как правило, не являются гармоническими, тем не менее гармоническое воздействие широко используется как удобный тестовый сигнал. Гармонический сигнал является единственным физически реализуемым сигналом, который при прохождении через линейную цепь не меняет своей формы (меняется лишь амплитуда и появляется фазовый сдвиг, рис. 2.13).
Рис.
2.13. Реакция цепи
на гармоническое
воздействие
С другой стороны, определяя реакцию цепи на гармонические сигналы разных частот (от низких до высоких), можно определить степень инерционности (быстродействие) цепи, т. к. максимальная скорость изменения гармонического сигнала во времени пропорциональна частоте:
x(t)
=
xm
sin
t;
![]() =
xm
cos
t;
=
xm
cos
t;
![]() =
xm.
=
xm.
При частотном анализе широко используется символический метод (метод комплексных амплитуд), при котором реальный гармонический сигнал
x(t) = xm sin t
заменяется символическим (физически не существующим) комплексным экспоненциальным воздействием:
![]() . (2.9)
. (2.9)
Такая замена возможна только для линейной цепи, в которой справедлив принцип суперпозиции, и проводится с целью замены дифференциального уравнения цепи алгебраическим.
Действительно, дифференцирование и интегрирование (2.9) по времени приводят к следующим очевидным результатам:
![]()
т. е. к умножению или делению исходной функции на j.
Реакция цепи на символический сигнал ищется в виде
![]() (2.10)
(2.10)
где
![]() – некоторый комплексный оператор.
– некоторый комплексный оператор.
Представляя
в (2.10)
![]() в показательной форме
в показательной форме
![]() ,
,
где
()
– аргумент
![]() ;K()
– модуль
;K()
– модуль
![]() ,
,
получаем
![]()
![]() .
.
Таким образом, искомая реакция
![]()
Итак,
определив
![]() ,
его модульК(),
аргумент (),
задача решается однозначно.
,
его модульК(),
аргумент (),
задача решается однозначно.
Рис.
2.14. Графики АЧХ и ФЧХ
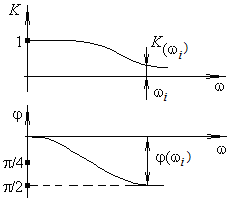
![]() называетсяамплитудно-фазовой
частотной характеристикой цепи (АФЧХ),
зависимость
называетсяамплитудно-фазовой
частотной характеристикой цепи (АФЧХ),
зависимость
![]() называетсяамплитудной
частотной характеристикой
(АЧХ),
называетсяамплитудной
частотной характеристикой
(АЧХ),
![]() – фазовой частотной
характеристикой (ФЧХ), рис. 2.14.
– фазовой частотной
характеристикой (ФЧХ), рис. 2.14.
Очень важным является то обстоятельство, что параметры К() и () могут быть определены экспериментально для сколько угодно сложной цепи, что широко применяется на практике.
Продемонстрируем на простом примере алгоритм частотного анализа. Пусть имеется цепь, связь «вход-выход» которой описывается дифференциальным уравнением
![]() .
.
Введем символические значения
![]() ,
,
подстановка которых в дифференциальное уравнение приводит к равенству
![]()
откуда получим
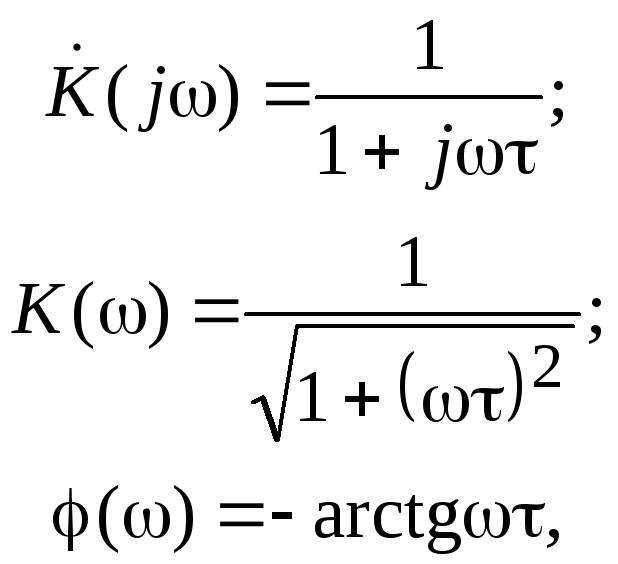 (2.11)
(2.11)
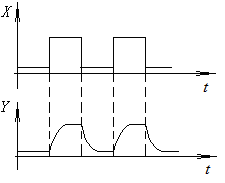
Рис. 2.15. Прохождение
импульсного
сигнала через цепь с
«завалом» АЧХ
в области высоких частот
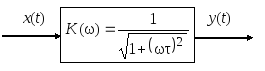
![]()
На основе (2.11) можно построить график АЧХ и ФЧХ (см. рис. 2.14), по которому определяется реакция цепи на гармоническое воздействие любой частоты (i).
Кроме того, АЧХ позволяет сделать вывод о том, что данная цепь плохо пропускает высокочастотные сигналы, т. е. сложный сигнал, проходя через такую цепь, «потеряет» высокочастотные составляющие. На рис. 2.15 показано изменение формы сигнала при прохождении через цепь с АЧХ на рис. 2.14.
