
методичка2692(вища.матем
.).pdfМІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ СУМСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ
2692 Методичні вказівки до практичних занять з курсу
«Вища математика»
з теми
«Елементи лінійної та векторної алгебри. Аналітична геометрія»
для студентів інженерних спеціальностей денної форми навчання
СУМИ Видавництво СумДУ
2009
Методичні вказівки до практичних занять з курсу «Вища математика» з теми «Елементи лінійної та векторної алгебри. Аналітична геометрія» / Укладачі: Т.В. Завальна, Н.І. Одарченко, О.В. Бондар. – Суми: Вид-во СумДУ, 2009. – 134 с.
Кафедра математичного аналізу і методів оптимізації
Навчальне видання
2692 Методичні вказівки
до практичних занять з дисципліни «Вища математика» з теми
«Елементи лінійної та векторної алгебри. Аналітична
геометрія»
для студентів інженерних спеціальностей денної форми навчання
Відповідальний за випуск В.О. Ячменьов Редактор Н.О. Кравченко
Комп’ютерне верстання О.В. Бондара
Формат 60х84/16. Ум. друк. арк. 7,91. Обл. – вид. арк. 4,62. Тираж 50 пр. Зам. №
Видавець і виготовлювач Сумський державний університет,
вул. Римського-Корсакова, 2, м. Суми, 40007 Свідоцтво суб’єкта видавничої справи ДК № 3062 від 17.12.2007
ТЕМА: РІВНЯННЯ ПЛОЩИНИ В ПРОСТОРІ
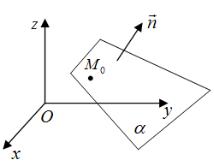
1 Рівняння площини, що проходить через дану точку, перпендикулярно даному вектору (рис. 1):
Рис. 1
A(x − x0 )+ B(y − y0 )+ C(z − z0 ) = 0 ,
де n = (A; B;C ), M 0 (x0 ; y0 ; z0 ), n – нормальний вектор площини.
2 Загальне рівняння площини
Ax + By + Cz + D = 0 .
Частинні випадки загального рівняння площини:
1 Якщо D = 0 , то Ax + By + Cz = 0 . У цьому випадку площина проходить через початок координат.
2 Якщо C = 0 , то Ax + By + D = 0 . Нормальний вектор n = (A; B;0) перпендикулярний до осі oz . Площина паралельна осі oz . Якщо ж B = 0 , то площина паралельна осі oy , A = 0 – паралельна осі ox .
3 Якщо C = D = 0 , то Ax + By = 0 проходе через вісь oz . Аналогічно, рівнянням By + Cz = 0 і Ax + Cz = 0 відповідають площини, що проходять відповідно через вісі ox і oy .
3
4 Якщо |
A = B = 0 , то |
Cz + D = 0 , така |
площина |
|||
паралельна |
площині oxy . Аналогічно, |
рівнянням |
||||
Ax + D = 0 і By + D = 0 відповідають площини, |
паралельні |
|||||
відповідно площинам oyz і oxz . |
|
|
||||
5 Якщо |
A = B = D = 0 , то Cz = 0 , |
z = 0 , це рівняння |
||||
площини oxy . Аналогічно |
By = 0 , |
y = 0 , |
рівняння |
|||
площини oxz ; |
x = 0 – |
рівняння площини oyz . |
|
|||
3 Рівняння площини, що проходить через три дані |
||||||
точки M1 (x1 ; y1 ; z1 ); M 2 (x2 ; y2 ; z2 ) ; M 3 (x3 ; y3 ; z3 ): |
||||||
|
x − x1 |
y − y1 |
z − z1 |
|
|
|
|
|
|
|
|||
|
x2 − x1 |
y2 − y1 |
z2 − z1 |
= 0 . |
|
|
|
x3 − x1 |
y3 − y1 |
z3 − z1 |
|
|
|
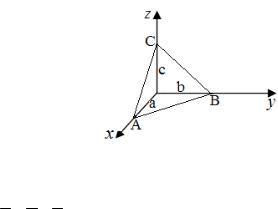
4 Рівняння площини у «відрізках» на осях (рис. 2):
Рис. 2
x + y + z = 1 . a b c
5 Кут між двома площинами. Умова паралельності і перпендикулярності двох площин. Нехай задані дві площини α1 і α 2 (рис. 3):
4
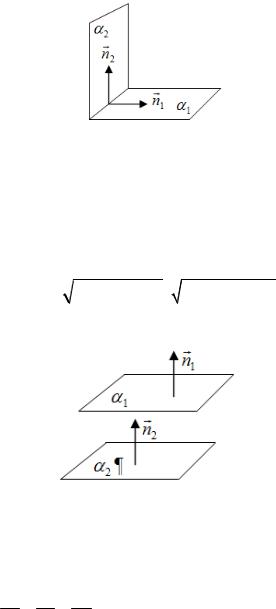
Рис. 3
A1 x + B1 y + C1 z + D1 = 0 ,
A2 x + B2 y + C2 z + D2 = 0 .
За кут між площинами |
α1 і |
α 2 беруть кут між |
||||||||
нормальними векторами n = (A1 ; B1 ;C1 ), |
n = (A2 ; B2 ;C2 ): |
|||||||||
cosφ = |
|
|
A1 A2 + B1B2 |
+ C1C2 |
|
. |
||||
|
|
|
|
|
|
|
|
|
||
|
|
A 2 |
+ B 2 + C 2 × |
A 2 |
+ B 2 |
+ C 2 |
||||
1 |
1 |
1 |
|
|
2 |
2 |
2 |
|
||
Якщо площини α1 і α 2 перпендикулярні, то перпендикулярні і їх нормалі (рис. 4). Тоді
Рис. 4
n1 × n2 = 0 A1 A2 + B1 B2 + C1C2 = 0 .
Якщо площини α1 і α 2 паралельні, то будуть паралельні і їх нормалі n1 і n2 .
Тоді A1 = B1 = C1 .
A2 B2 C2
5
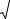
6 Відстань від точки до площини визначається
формулою |
|
|
+ By0 |
+ Cz0 |
+ D |
|
|
|
|
d = |
|
Ax0 |
|
|
. |
||||
|
|
||||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
A2 + B2 + C 2 |
||||||
6

Площина в просторі. Приклади
Приклад 1 Скласти рівняння площини, що проходить через точку M 0 (2;1;−1) перпендикулярно до вектора a = {1;2;3} .
Згідно з умовою задачі вектор a перпендикулярний до площини, а тому є її нормальним вектором n = {1;2;3} . Використавши рівняння
A(x − x0 )+ B(y − y0 )+ C(z − z0 ) = 0 , матимемо
1× (x - 2) + 2 × (y -1)+ 3 × (z + 1) = 0 або x + 2 y + 3z −1 = 0 . |
|
|
|||||||||||||||||||||||||||||||
|
Приклад 2 |
|
|
Скласти |
|
рівняння |
|
|
площини, |
що |
|||||||||||||||||||||||
проходить через точку M 0 (2;1;−1), |
перпендикулярно |
до |
|||||||||||||||||||||||||||||||
вектора |
|
|
|
|
|
, де M 1 (4;2;3), |
M 2 (5;-2;1) . |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
M1M 2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
Оскільки |
площина перпендикулярна |
до |
вектора |
|||||||||||||||||||||||||||||
|
|
= {5 − 4;−2 − 2;1− 3} = {1;−4;−2} , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
M1M 2 |
то |
цей |
вектор |
є |
її |
|||||||||||||||||||||||||||
нормальним вектором |
|
|
|
|
= {1;−4;−2} , а |
|
|
тому |
згідно |
з |
|||||||||||||||||||||||
n |
|||||||||||||||||||||||||||||||||
формулою (1) маємо: 1× (x - 2) - 4 × (y -1) - 2 × (z +1) = 0 |
або |
||||||||||||||||||||||||||||||||
|
x − 4 y − 2z = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Приклад 3 |
|
|
Скласти |
|
рівняння |
|
|
площини, |
що |
|||||||||||||||||||||||
проходить через точки |
M 1 (2;4;1) |
|
і M 2 (0;-2;4) паралельно |
||||||||||||||||||||||||||||||
вектору |
|
= {2;1;−1} . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Точка M (x; y; z ) належить |
шуканій |
|
|
площині тоді і |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
тільки тоді, коли вектори M1M , |
|
M1M 2 та |
|
|
компланарні, |
||||||||||||||||||||||||||||
|
a |
||||||||||||||||||||||||||||||||
тобто ( |
|
|
|
|
|
|
|
|
|
|
)= |
|
x − 2 |
|
y − 4 |
z −1 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
, |
|
, |
|
|
|
− 2 |
|
− 6 |
3 |
|
|
= 0 , |
|
|
|
|||||||||||||||||
M1M |
M1 M 2 |
|
|
|
|
|
|
||||||||||||||||||||||||||
a |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
−1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
або 3x + 4 y + 10 z − 32 = 0 .
7
Приклад 4 |
Скласти рівняння площини, що |
проходить через |
точку M0 (3;4;−5) паралельно двом |
векторам a1 = {3;1;−1} , a2 = {1;−2;1} .
Точка |
|
M належить |
шуканій площині тоді і |
тільки |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
= (x − 3; y − 4; z + 5), |
|
|
|
|
|
||||
тоді, коли |
вектори |
|
M 0 M |
та |
|
2 |
|||||||||||||
|
a1 |
a |
|||||||||||||||||
компланарні. Отже |
x − 3 |
y − 4 |
z + 5 |
|
|
|
|
|
|
|
|||||||||
( |
|
|
|
|
|
2 )= |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
, |
|
|
|
|
3 |
1 |
−1 |
|
= 0 , |
|
|
|
||||||
M 0 M |
|
|
|
||||||||||||||||
a1 , |
a |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
− 2 |
−1 |
|
|
|
|
|
|||
тобто x + 4 y + 7 z + 16 = 0 . |
|
|
|
|
|
|
|
|
|||||||||||
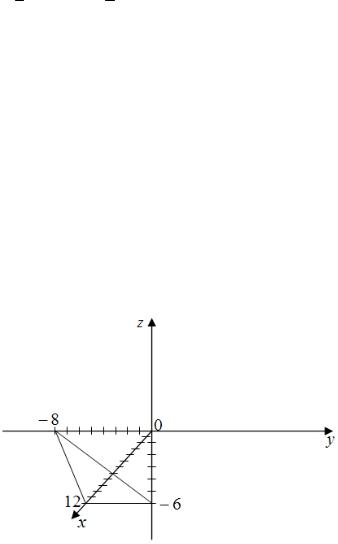
Приклад 5 |
Побудувати |
площину2x −3y −4z −24= 0, |
|||||||||||||||||
записавши її рівняння у відрізках на осях.
Запишемо для заданої площини її рівняння «у
відрізках». Маємо |
2x |
− |
3y |
− |
4z |
= 1, або |
|
x |
+ |
y |
+ |
z |
= 1 , |
24 24 24 |
|
12 |
|
− 8 |
− 6 |
||||||||
де a = 12 , b = −8 , c = −6 . |
|
|
|
|
|
|
|
||||||
Рис. 5
8

|
Приклад 6 |
|
Скласти |
рівняння |
площини, |
що |
||||||||||||||
проходить |
через |
|
три точки M 1 (3;0;4) , |
|
M 2 (5;2;6), |
|||||||||||||||
|
M3 (2;3;−3). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Нехай M (x; y; z ) - довільна точка |
площини. |
Тоді |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= {x - 3; y; z - 4} , |
|
|
|
|
|
= {2;2;2} , |
||||
вектори |
|
|
M1M |
|
|
|
M1M 2 |
|||||||||||||
|
|
|
= {−1;3;−7} |
|
|
|
|
|
||||||||||||
|
M1M 3 |
є компланарними, |
тому |
|
їх мішаний |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x - 3 |
y |
z - 4 |
|
= 0 . |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
добуток дорівнює нулю. Тобто |
2 |
2 |
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
-1 3 - 7 |
|
|
|
|
||||
|
Звідси маємо 5x − 3 y − 2 z − 7 = 0 . |
|
|
|
|
|
|
|
||||||||||||
|
Приклад 7 |
|
Обчислити |
відстань |
між |
|
площинами |
|||||||||||||
2x − 3 y + 6z − 21 = 0 і 4x − 6 y + 12 z + 35 = 0 . |
|
|
|
|
||||||||||||||||
|
Дані площини паралельні, оскільки |
|
|
|
|
|
|
|||||||||||||
|
2 |
= |
− 3 |
= |
6 |
¹ − 21 . Щоб знайти відстань між ними, |
||||||||||||||
4 |
- 6 |
|
||||||||||||||||||
|
12 |
|
35 |
|
|
|
|
|
|
|
|
|
||||||||
візьмемо на одній із них точку і знайдемо відстань від неї до іншої площини. Нехай, наприклад, у першому рівнянні x = 0 ; z = 0 , тоді y = −7 . Таким чином, точка (0;−7;0) лежить на першій площині. Скористаємося формулою для визначення відстані від точки до площини:
d = |
|
|
4 × 0 - 6 × (-7) +12 × 0 + 35 |
|
|
= |
|
|
|
|
|
|
||||||||||||
|
|
77 |
|
= |
77 |
= 5,5 . |
||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
42 + (-6)2 +122 |
|
|
|
|
|
196 |
14 |
|
||||||
Приклад 8 |
Обчислити кут |
|
між |
|
площинами |
|||||||||||||||||||
x + 2 y − z + 5 = 0 і 2x − y + z − 3 = 0 . |
|
|
|
|
|
|
|
|||||||||||||||||
Кут |
|
|
|
між |
|
площинами |
визначається |
за |
формулою |
|||||||||||||||
cosϕ = |
|
n1n2 |
|
|
|
= (1;2;−1); |
|
|
= |
(2;−1;1), то |
||||||||||||||
|
|
|
|
|
|
|
. |
Оскільки |
n1 |
|
n2 |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
n1 |
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9
