
- •Введение
- •Глава 2. Параллактический треугольник светила и его решение
- •§4. Параллактический треугольник и его решение по основным формулам
- •§5. Вычисление высоты и азимута светила по системам формул
- •§7. Разложение высоты и азимута в ряд Тейлора. Теория таблиц численного типа
- •§1. Небесная сфера
- •§2. Системы сферических координат
- •§3. Графическое решение задач на небесной сфере
- •Глава 3. Видимое суточное движение светил. Изменение координат светил
- •§9. Характеристика суточного движения светил
- •§10. Явления, связанные с суточным движением светил
- •§11. Изменение координат светил вследствие видимого суточного движения
- •Глава 4. Обращение Земли вокруг Солнца. Видимое движение Солнца и изменение его координат
- •§13. Обращение Земли по орбите и видимое годовое движение Солнца
- •§14. Изменение экваториальных координат Солнца в течение года
- •Глава 5. Орбитальное и видимое движение планет, Луны и искусственных спутников
- •§18. Фазы и возраст Луны
- •§21. Орбитальное движение искусственных спутников
- •Глава 6. Измерение времени
- •§22. Основы измерения времени
- •§23. Звездные сутки. Звездное время. Основная формула времени
- •§26. Поясное, декретное, летнее, московское и стандартное времена, их связь с местной системой
- •§28. Понятие о точных шкалах времени
- •Глава 7. Вычисление видимых координат светил. МАЕ
- •§31. Понятие о вычислении видимых координат светил на ЭВМ
- •§32. Устройство таблиц МАЕ для расчета часовых углов и склонений светил
- •§33. Определение времени кульминации светил
- •§34. Обоснование расчета времени видимого восхода (захода) Солнца и Луны и времени сумерек
- •§35. Определение времени восхода и захода Солнца и Луны и времени сумерек по МАЕ
- •Глава 8. Измерители времени. Судовая служба времени
- •Глава 9. Звездное небо. Звездный глобус
- •§42. Устройство звездного глобуса, его установка. Понятие о других пособиях
- •§43. Решение задач с помощью звездного глобуса
- •Глава 10. Секстан
- •§44. Основы теории навигационного секстана
- •§45. Устройство навигационных секстанов
- •§46. Понятие об инструментальных ошибках секстана и их учете
- •§47. Понятие о секстанах с искусственным горизонтом
- •Глава 11. Наблюдения с навигационным секстаном
- •§48. Выверка навигационного секстана на судне
- •§50. Приемы измерения высот светил над видимым горизонтом
- •§53. Наклонение видимого горизонта. Наклонение зрительного луча
- •§55. Общий случай исправления высот светил, измеренных над видимым горизонтом
- •§56. Частные случаи исправления высот светил
- •§57. Приведение высот светил к одному зениту (месту) и одному моменту
- •§58. Определение средних квадратических ошибок поправок и измерения углов
- •§59. Определение средней квадратической ошибки измерения высот светил в море
- •Глава 13. Астрономическое определение поправки компаса
- •§60. Основы астрономического определения поправки компаса
- •§62. Пеленгование светил. Точность поправки компаса
- •§63. Определение поправки компаса. Общий случай
- •Глава 14. Теоретические основы определения места судна по светилам
- •§65. Общие принципы астрономического определения места
- •§67. Метод линий положения. Высотная линия положения
- •§72. Ошибки в высотной линии. Оценка ее точности и вес
- •Глава 16. Методы отыскания места судна и оценки его точности при наличии ошибок в высотных линиях
- •Глава 17. Определение места по одновременным наблюдениям светил. Общий случай
- •§76. Особенности определения места по одновременным наблюдениям светил
- •§77. Общий случай определения места по звездам
- •§78. Определение места днем по одновременным наблюдениям Луны и Солнца
- •§79. Определение места днем по одновременным наблюдениям Венеры и Солнца
- •§80. Определение места по одновременным наблюдениям Венеры, Луны и Солнца
- •Глава 18. Определение места судна по разновременным наблюдениям Солнца
- •§81. Особенности определения места по разновременным наблюдениям Солнца
- •§82. Влияние ошибок счисления и наивыгоднейшие условия для определения места по Солнцу
- •§83. Определение места по Солнцу в общем случае
- •§84. Определение места комбинированием навигационных и астрономических линий положения
- •Глава 19. Ускоренные способы обработки наблюдений
- •§86. Обзор приемов ускорения обработки наблюдений
- •§87. Прием перемещения счислимого места
- •§88. Определение места с предварительной обработкой (предвычислением) линий положения
- •§92. Решение астрономических задач на клавишных ЭВМ
- •Глава 20. Частные методы определения координат места судна
- •§93. Определение широты места по меридиональной и наибольшей высотам Солнца. Понятие о близмеридиональных высотах
- •§96. Определение координат места в малых широтах по соответствующим высотам Солнца
- •§97. Графический способ определения места при высотах Солнца, больших 88°
- •§98. Особенности определения места в высоких широтах
- •Глава 21. Перспективы развития методов астрономических определений в море. Краткий исторический очерк
- •§99. Понятие об астронавигационных системах и навигационных комплексах
- •§100. Краткий очерк истории мореходной астрономии
- •Список литературы

§11. ИЗМЕНЕНИЕ КООРДИНАТ СВЕТИЛ ВСЛЕДСТВИЕ ВИДИМОГО СУТОЧНОГО ДВИЖЕНИЯ
Примем, что суточное вращение сферы происходит равномерно (о неравномерностях вращения Земли упоминалось в §9, учет их показан в §28), и выясним, какие из координат светил изменяются вследствие суточного движения. Вращение сферы оценивается по смещению какой-либо точки или светила от неподвижного меридиана наблюдателя, т.е. вестовым часовым углом (рис. 20). Поэтому при равномерном вращении сферы часовые углы светил также изменяются равномерно, пропорционально повороту сферы или приближенно — пропорционально времени1. Склонение светила отсчитывается от экватора до параллели, которая является суточным путем светила, поэтому в суточном движении δ не меняется. Прямое восхождение светила отсчитывается по экватору от точки Овна, но она связана со сферой и участвует в ее суточном вращении, поэтому α не меняется. Следовательно, в суточном движении из экваториальных координат меняются только часовые углы; δ и α не меняются; этим объясняется их удобство для составления звездных карт. Высота и азимут светила при его движении по параллели аа1 (см. рис. 20) изменяются. Вследствие того, что часовой угол светила меняется равномерно, примем t за независимую переменную и найдем приращения горизонтных координат ∆h и A в функции от приращения ∆t часового угла. Светило С в суточном движении перемещается по параллели аа1 и занимает положения С, С1. Проводя меридианы PC и РС1 видим, что t в полукруговом счете изменился на величину +∆t. Построив вертикалы zC и rС1 видим, что высота изменилась от h до h1 на величину —∆h, а азимут в полукруговом счете — на величину —∆А.
1 Изменение часового угла во времени включает еще учет собственного движения светила и движения наблюдателя по Земле, (см. § 93). Вследствие этого изменение t можно считать пропорциональным времени только за малый промежуток времени.
59
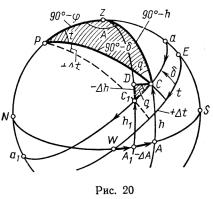
Графический вывод формул изменения высоты и азимута. Изменение высоты. Проведя альмукантарат CD на рис. 20, получим на сфере малый ∆CDC1, в котором CD=—∆h, угол С равен q; гипотенуза СС1 и катет DC являются дугами малых кругов, которые меньше соответствующих дуг
больших кругов в cos δ и cos h раз. На этом основании имеем: |
|
||||
|
|
СС1=∆t cos δ |
(*) |
||
и |
|
|
|
|
|
|
CD = — ∆A cos h |
(**) |
|||
Принимая ∆CC1D за плоский, найдем C1D: |
|
||||
|
C1D =СС1 sin q, |
|
|||
или, подставляя вместо СС1 формулу (*), получим |
|
||||
—∆h=∆t cos δ sin q |
(41) |
||||
Заменим δ и q более удобными для анализа координатами, для чего к |
|||||
параллактическому ∆PzC применим формулу синусов |
|
||||
|
sin q |
= |
sin A |
|
|
|
sin(900 −ϕ) |
sin(900 −δ) |
|
||
|
|
|
|||
или
sin q cosδ = sin A cos φ
Подставляя это выражение в формулу (41), получим окончательно
∆h= –sin A cos φ ∆t (42)
Вследствие сделанных допущений эта формула справедлива только при достаточно малых ∆t; более точную формулу получим ниже с помощью рядов.
60
Примечание. При круговом счете азимутов и часовых углов формула (42) имеет вид
∆h= sin A cos φ ∆t
где величину sin А надо исследовать на знаки, а ∆t всегда положительно.
Изменение азимута. Из малого ∆СОС1 имеем |
|
CD = СС1 cos q. |
|
Заменяя CD и СС1 выражениями (**) и (*), получим: |
|
—∆А cos h =∆t cosδ cos q |
|
или |
|
∆А=—cos δ cos q sec h∆t |
(43) |
Заменим координаты δ и q на горизонтные, для чего к параллактическому |
|
∆PzC (см. рис. 20) применим формулу пяти элементов к углу q: |
|
cosq sin (90°—δ)=sin (90°—h) cos (90°—φ) — cos (90°—h)sin (90°—φ)cos A |
|
или после упрощений получим |
|
cos q cos δ = cos h sin φ — sin h cos φ cos A |
(44) |
Подставляя в выражение (43) вместо cos q cos δ правую часть формулы
(44), имеем
∆A = −cosh sinϕ − sinh cosϕcos A ∆t cosh
после деления на cos h получим окончательно
∆A= —(sinφ — tg h cos A cos φ) ∆t (45)
Эта формула справедлива лишь при достаточно малых ∆t.
Примечание. При круговом счете азимутов и t формула (45) имеет знак «+» в северной и «—» в южной широтах.
Вывод формул ∆h и ∆А с помощью рядов Тейлора. Применим ряд
Тейлора для отыскания приращений ∆h и ∆А в функции часового угла:
∆h = |
dh |
∆t + |
1 |
|
d 2 h |
∆t 2 |
|
+... |
|
|
||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
dt |
|
2 dt |
|
|
|
|
|
(46) |
|||||
|
|
|
|
|
|
|
|
|||||||
|
dA |
|
1 d 2 A |
|
|
|
|
|||||||
∆A = |
∆t + |
∆t |
2 |
|
|
|
||||||||
dt |
2 dt |
2 |
|
|
+... |
|
||||||||
|
|
|
|
|
|
|
|
|
||||||
Эти ряды представляют частный случай формул (13), (14) из §7, причем
61
для ∆А обычно ограничиваются первым членом. Производные |
dh |
|
, |
d 2h |
и |
dA |
||
dt |
dt 2 |
dt |
||||||
|
|
|
|
|||||
dA |
– получены в том же §7 (формулы (20), (29), (25)). Здесь |
|
dh |
и |
dA |
|||
dt |
|
|
|
|
dt |
|
dt |
|
представляют скорости изменения высоты и азимута в суточном движении ωh и
ωА, а |
d 2 h |
— ускорение в движении по высоте. Подставляя их значения в ряды |
|||
dt 2 |
|||||
|
|
|
|
||
146), получим: |
∆t 2 |
|
|||
|
|
∆h= –cos φ sin А ∆t + cos φ соs A cos δ cos q sec h |
(47) |
||
|
|
2 |
|||
|
|
|
|
||
и
∆А= –cos q cos δ sec h∆t
или с учетом формулы (44)
∆А= –(sin φ — tg h cos A cos φ) ∆t (48)
Очевидно, формула (47) представляет уточненную формулу (42), а формула (48) та же, что (45). Ошибки формул (47), (48) обычно оцениваются величиной отброшенных членов ряда (46).
Исследование формулы изменения высоты (47). 1. Приращение высоты зависит от положения светила по азимуту. Выясним, при каких А высота светила изменяется быстрее.
На первом вертикале (при А=90°, 270°) второй член формулы (47) равен нулю и ∆h=±cosφ∆t; скорость изменения ωh — наибольшая. На меридиане (при A=0°,180°) первый член формулы равен нулю, а второй — наибольший, т.е. ускорение наибольшее, ωh=0.
Следовательно, на первом вертикале высота изменяется быстро и равномерно, в самой кульминации — не меняется, а около — меняется медленно и неравномерно. Практически это означает, что около первого вертикала можно осреднять серии высот за большой ∆t, а около меридиана — за малый ∆t.
2. Приращение высоты зависит от широты места. При φ=90° имеем ∆ht=0, т.е. на полюсах высоты не меняются. При φ=0°∆ht, может иметь наибольшее значение (при A=90°), равное изменению часового угла, т.е. ∆h=—∆t.
62
Следовательно, приращение высоты меняется от 0 до ±∆t.
Практическое применение формулы изменения высоты. Выразим в первом члене формулы (47) ∆h в градусных минутах ('), а ∆t — в часовых секундах (с), учитывая, что 1’=4c, получим практическую формулу
∆h' = −0,25cosϕsin A∆tc |
(49) |
t |
|
По этой формуле, умноженной на 10, составлена таблица 17 МТ—75 (табл. 15-6 в МТ—63). Эти таблицы применяются при контроле серии наблюдений по разностям и при приведении высот к одному моменту.
Пример 13. =43°50' N; A=30,5° SO; ∆tost=1М21С=81c (с «—»). Определить
∆h.
Решение. Из таблицы 17 МТ—75 имеем ∆h за 10c=0,90' ∆h'=(–0,90)·(– 8,1)=+7,3'.
Исследование формулы изменения азимута. Установим, на каких участках суточного пути азимут изменяется быстрее. При А=180° в формуле (48) внутри скобок получится «+», а при А=90° второй член равен 0. Следовательно, азимут меняется быстрее около верхней кульминации. Отсюда вытекает следствие — для получения наибольшей разности азимутов, например Солнца, его надо наблюдать до и после кульминации (т.е. в φN от SO до SW). Медленнее всего азимут изменяется от восхода до первого вертикала, а в элонгации — не меняется.
Установим, как влияет на ∆А широта места. При φ=90° ∆А=—∆t, а при φ=0 ∆А= tgh cos A ∆t (при А=180° ∆А=tg H ∆t). Следовательно, на экваторе и в тропиках азимут меняется крайне неравномерно — от 0 до мгновенного изменения на 180° (при H=90°), а на полюсе — равномерно так же, как ∆t.
Практическое применение формулы ∆А. В МТ—75 приведена табл. 18
для изменения азимута за 10c времени, рассчитанная по формуле
∆А't=—0,25 (sin φ — cos φ tg h cos A) ∆tc (50)
умноженной на 10. По этой таблице можно получить скорость изменения азимута ωA в данный момент. В МТ—63 таблица 15-г дает ∆А° за 1м.
Пример 14. φ=30° N; А=145°; h=60°. Определить скорость изменения
63
азимута.
Решение. Из таблицы 18 МТ—75 получим ωA=4,3710c или 0,4°/м. Практически удобнее для наших задач ωA получать по таблицам ВАС—58.
64
