где SГР и α* вычислены по формулам (96) и (99).

Приведенные приемы расчета эфемерид Солнца и звезд дают достаточно точные для мореходной астрономии координаты в течение 15—20 лет от начальной эпохи, и их сравнительно легко реализовать на ЭВМ. Существуют и другие алгоритмы получения эфемерид, зависящие от поставленных задач и типа ЭВМ.

На судовых ЭВМ данного поколения нет смысла вычислять различные частные задачи, например кульминации, восходы светил, элементы освещенности и другие, поэтому, независимо от наличия машины, на судне требуется МАЕ.

§32. УСТРОЙСТВО ТАБЛИЦ МАЕ ДЛЯ РАСЧЕТА ЧАСОВЫХ УГЛОВ И СКЛОНЕНИЙ СВЕТИЛ

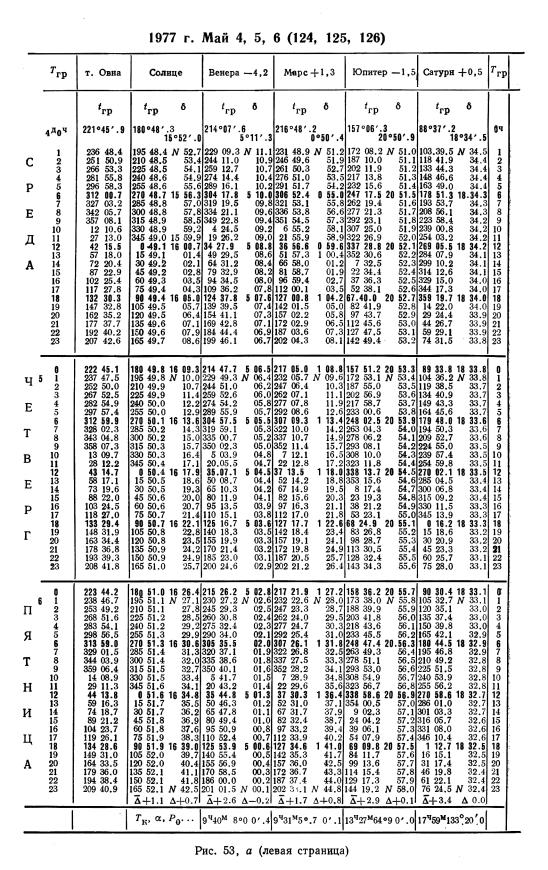
Основные данные помещены в ежедневных таблицах МАЕ, занимающих большую его часть. На каждом развернутом листе МАЕ приведены данные для трех суток: на левой странице — часовые углы точки Овна (звездное время), часовые углы и склонения Солнца, Венеры, Марса, Юпитера и Сатурна; на правой странице — часовые углы и склонения Луны, время ее восхода и захода на каждый день, время восхода, захода Солнца и сумерек на среднюю дату листа (рис. 53). Внизу страниц приведены дополнительные данные: время кульминации, параллаксы, радиусы и др. Рассмотрим принцип устройства таблиц МАЕ для часовых углов и склонений светил.

136

Получение звездного времени. Аргументами для входа в МАЕ являются гринвичская дата, Тгр и название светила, поэтому найдем зависимость, связывающую часовой угол точки Овна с Тгр. Применяя основную формулу времени к среднему Солнцу, получим:

SГР=tГР9+α9

или

так как

SГР= tГРE, а tГР9=TГР±12ч

По формуле (101) для значений Тгр через 1Ч предвычислены и помещены в МАЕ табличные значения tт точки Овна (помечены tгр). Поправка за избыток ∆T сверх часа получается дифференцированием формулы (101) по Т. Переходя к конечным приращениям и взяв величину ∆α9 за 60м, получим

∆tГРE/∆Т=1+ ∆α9/60м

откуда

∆tГРE=∆Т+(∆α9/60м) ∆Т

звездные единицы и в градусную меру.

Поправки, рассчитанные по формуле (102), помещены в конце МАЕ в «Основных интерполяционных таблицах» (ОИТ) на каждую минуту и секунду часа. В таблицу входят с минутами ∆Т (сверху) и секундами (слева) в графу «Точка Овна». Выбрав ∆tE, придают ее к часовому «табличному» значению tT и далее получают местное звездное время

Вычисления производят по схеме, показанной в примере 25. Величину SM

139

определяют при подборе звезд по звездному глобусу или таблицам, а также как промежуточную величину при определении tM* .

Пример 25. 5 мая 1977 г. в Тc=5ч53м (№=8Оst); λ=103°50', 2Оst; Txр=9ч52м47с; u=+28'. Определить tME (SM).

Решение

Получение часовых углов и склонений звезд. Формула для часового угла звезды получается из основной формулы времени решением ее относительно tM* :

tM* =SM–α*= tME+τ*

где τ*=360°—α*

Подставляя в эту формулу значение tME из формулы (103), получим tM* =tM+∆tE±λ+τ* (104)

Величины τ*, а также δ* приведены в разделе МАЕ, озаглавленном «Звезды. Видимые места» (с. 270 МАЕ), для 159 наиболее ярких звезд в порядке возрастания их α. На левой странице по прямому восхождению, номеру и месту звезды в созвездии приведены τ* — градусы на год, минуты по месяцам. На правой странице по номеру и собственному имени звезды (если оно есть) приведены δ*. Так как минуты τ* и δ даны на первое число месяца, на промежуточные даты приходится интерполировать их между колонок. На вкладыше к МАЕ (приложение IV) величины τ и δ для 50 наиболее ярких звезд

140

приведены через 10 дней, поэтому интерполировать их не нужно, так как их значения точнее, чем в основных таблицах. Названия созвездий и звезд, их номера в МАЕ отыскиваются при необходимости на обратной стороне карты звездного неба, прилагаемой к Ежегоднику (приложение V к МАЕ).

Пример 26. 5 мая 1977 г. около Тс=19Ч52М (№=7W); λ=95°47,0' W

наблюдали α Волопаса; Тхр=2Ч50М38С; и=+1М48С,0. Определить t*M и δ*. Решение.

Получение часовых углов и склонений Солнца, планет и Луны.

Формулу, выражающую часовой угол через аргумент Тгр, можно получить из основной формулы времени, записав ее два раза — для среднего Солнца и для данного светила:

SГР=t9ГР+α9

SГР=tСВГР+αСВ

В один и тот же момент левые части равны, поэтому

tГРСВ +αСВ = tГР +α

или

tГРСВ = tГР +α −αСВ

но по формуле (72) имеем: tГРСВ =ТГР±12ч

Подставляя значение tГР , получим формулу для часового угла светила:

141

По этой формуле для Тгр через интервал в 1Ч предвычислены табличные значения tT часовых углов Солнца, четырех планет и Луны, помещенные в ежедневных таблицах МАЕ в колонке tГР. Приращение часового угла за промежуток ∆Т сверх целого часа ТГР получается следующим путем. Дифференцируя выражение (105) по Т и переходя к конечным приращениям, получим

∆∆Tt =1 + ∆∆αT − ∆α∆ТСВ

Принимая изменения прямых восхождений за 1Ч=60м и прибавив и отняв

разделено на две части: равномерную ∆t1 (в первых скобках), не зависящую от даты, и неравномерную ∆t2, меняющуюся по датам. В величину ∆t1 входят: ∆α — изменение прямого восхождения среднего Солнца за час, равное 2,5';

— наибольшее возможное изменение α данного светила за час: для Солнца 2,8'; для Венеры 3,5'; для Луны 43,5'. Величина ∆t1 представляет перевод промежутка ∆ТМ,С в равномерное изменение t, т.е. как бы во время,

считаемое по данному светилу. Для Солнца и планет величина ∆α — ∆αСВМАКС ,

представляющая как бы переводной коэффициент, принята в МАЕ одинаковой по наибольшему ∆ для Венеры, равному 3,5', поэтому второй член в скобках равен 1,0', а ∆t1 за час составит 14°59' и доли его за меньшие промежутки. Для Луны величина ∆α — ∆αСВМАКС составит 41,0', поэтому ∆t1 за час равна 14°19'.

Значения ∆t1 для Солнца (планет) и Луны вычислены для каждой минуты и секунды часа и приведены в ОИТ в отдельных колонках.

Вторая поправка ∆t2 учитывает неравномерность изменения α Луны,

142

Солнца и планет:

предвычислена для Луны на каждый час, а для Солнца и планет — на среднюю дату листа (приведена внизу колонок).

Квазиразностью ∆ в МАЕ называется разность между наибольшим возможным изменение α светила за 1Ч и фактическим изменением его за данный час. Квазиразность в нашем МАЕ всегда положительна, так как взято

∆αМАКС (в английском — для Венеры бывает отрицательна). Например, для

Солнца наибольшая ∆=3,5'—2,3'=1,2'; для Луны =18,0'; для планет ∆=6,0'. Квазиразность интерполируется на данную минуту, для чего надо войти с

выбранной ∆ и минутой ∆ТГР в две крайние колонки ОИТ. Полученная поправка ∆t2 дает отклонение изменения tCB данного светила от равномерного в данный час.

Вычисления производят по схеме, приведенной в примере 27. Склонение Солнца, Луны и планет приводится также через час, поэтому на промежуточное время его следует интерполировать в соответствии с формулой

где δ' — значение склонения на ближайший меньший час TГР, выбранное из ежедневных таблиц;

∆ — часовая разность склонений со своим знаком, выбираемая внизу колонки для Солнца и планет и рядом с δ — для Луны (иногда для Венеры и

143

Солнца ∆ следует образовать самому). Интерполирование производят по двум крайним колонкам ОИТ, входя в них с минутой ∆Т и ∆.

Пример 27. 4 мая 1977 г. в Тс=14ч30м (№=11W); λ=160°26' W, секундомер пущен в ТГРП =1Ч30М00С; наблюдали Солнце Тскм=2*48с. Определить t М и δ

Решение

Пример 28. 5 мая 1977 г. в Тс=543" (№=12 Оst); λс=166°25'Ost наблюдали Луну: Tхр=5Ч39М48С; u=+3М43С.

Определить tMe и δ. Решение.

144