3. Пропускна спроможність двійкового каналу зв’язку з перешкодами та без перешкод.

Пропускная способность канала святи без помех

Будем рассматривать канал передачи двоичных сигналов, когда любое сообщение является кодовой комбинацией из символов «0» и «1». Длительность сигналов «0» и «1» одинакова и равна Тс=1/В, где В – скорость модуляции.

Основные определения:

1. Средняя скорость передачи сообщений V (сообщ/сек) – среднее число символов, что передаются по каналу за одну секунду.

2. Скорость передачи информации С1 (бит/сек) – количество информации, что передается за одну секунду.

3. Пропускная способность канала С (бит/сек) – максимальное количество информации, что передается по данному каналу за секунду, т.е. С=С1макс.

При анализе дискретного канала без помех единственным показателем является наиболее эффективное использование пропускной способности канала.

Величина С1 характеризует среднее количество информации, что передается за секунду и определяется равенством: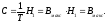

Тут Н(х) и Iх соответственно означают среднюю неопределенность и среднее количество информации при приёме сообщений длительностью Т. Если Т стремится к бесконечности то для определения средней скорости необходимо учитывать всю совокупность возможных сообщений. Будем считать что скорость передачи информации постоянна, и т.о. справедливо равенство: С₁=Н(х)/Т, при любом конечном Т.

Максимальное количество двоичных символов В_макс, что могут быть отправлены по каналу за 1 сек., зависит от электрических характеристик канала. Пропускная способность канала будет полностью использована, если среднее количество информации на один двоичный символ будет максимально. В этом случае для передачи сообщений будет нужно минимальное количество двоичных символов, и средняя длинна сообщения будет минимальна. Этого можно достигнуть , если символы «0» и «1» будут равномерными и независимыми друг от друга. В таком случае энтропия источника сообщений на один символ равна:

Н₁=log₂2=1 бит/сек. Это максимальное количество информации, что может нести один двоичный символ. Тогда пропускная способность канала для передачи двоичных символов без помех равно количеству элементарных посылок «0» и «1», что могут быть отправлены по каналу за 1 сек.

Пропускная способность канала святи с помехами

Существует два варианта определения пропускной способности канала с помехами:

1. Максимальное количество информации передаваемой по каналу с вероятностью ошибки не более некой допустимой величины.

2. Максимальное количество информации передаваемой по каналу передается абсолютно верно

При наличии помех среднее количество информации, что содержится в одном принятом элементарном сообщении равно:

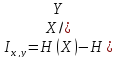
В таком случае скорость передачи информации по дискретному каналу без помех:

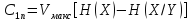
где 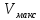– максимальное количество независимых сообщений, что может быть в среднем передано по каналу за 1 секунду.

Если свойства канала определяются как 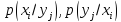то максимальную скорость передачи можно обеспечить путем выбора определенных ограничений, а именно оптимальное распределение вероятности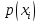, то есть путем выбора оптимального ансамбля сигналов. Относительно этого пропускная способность дискретного канала с помехами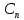как максимальную скорость передачи информации, что может быть достигнута при заданих свойствах канала, то есть :

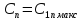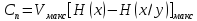
Где максимум берется по всем допустимым распределениям вероятности .

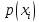Выражение пропускной способности 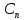может быть написано в нескольких формах. Можно записать: