3. Оптимальне кодування інформації. Алгоритми формування коду Хофмана та Шенона-Фано.

Оптимальное (эффективное) кодирование

Для полного использования пропускной способности канала необходимо осуществить эффективное кодирование, которое обеспечит устранение избыточности в сообщениях, что приходят от источника. Кодирование при котором обеспечивается полное использование пропускной способности канала называется оптимальным.

Первая теорема Шеннона дает ответ на вопрос, всегда ли можно осуществить оптимальное кодирование: если есть канал с пропускной способностью С, то сообщение из любого источника с энтропией Н(х)можно закодировать так, что окажется возможным передавать эти сообщения со скоростью как угодно близкой к С/Н(х) сообщений в секунду (С двоичных единиц за секунду. Рассмотрим справедливость теоремы для двоичного канала связи.

Пусть алфавит источника сообщений создает конечную систему.

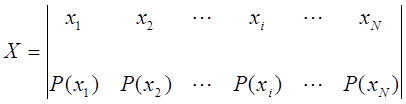
Для сообщения х_iдлинна кодовой комбинации равнаm_i, а вероятность ее появления Р(х_і). Количество информации что содержится в i-м сообщении равноI_xi=-logP(x_i). Пропускная способность канала будет полностью использована, если на каждыйдвоичный символ будет приходится один бит информации. Это будет в том случае, когда количество двоичных символов в кодовой комбинации будет равно количеству информации что содержится в ней. Таким образом, условием опримального кодирования является равенство.

Усреднив это сообщение повсем возможным сообщениям получим:

Меньше чем Н(х) средняя длинна сообщения быть не может.

Максимальная скорость что может быть достигнута в двоичном канале без помех равна:

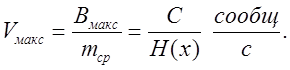
Оптимальные коды:

1. Код Шеннона-Фано

Все множество возможных сообщений записывается в порядке уменьшения вероятности их появления, а потом разбивается на две группы так, что бы суммы вероятностей в одной и во второй группе были примерно одинаковы. Первой цифрой для одной (н-р верхней) группы выбирается ноль, а для другой – единица или наоборот. После этого каждая группа разделяется на две подгруппы с приме6рно одинаковыми суммарными вероятностями, причем в верхних подгруппах следующей цифрой выбирают ноль, а в нижних – единицу.

Процесс повторяется до тех пор пока в каждой подгруппе не останется по одному сообщению. Оптимальность обеспечивается: 1) ни одна кодовая комбинация не может быть началом другой 2) так как при каждом разбиении мы приписываем к одной подгруппе ноль, а к другой единице, обеспечивается равномерное распределение нулей и единиц – необходимое условие полного использования пропускной способности канала, 3) При каждом разделении сообщений на две группы с примерно равными суммарными вероятностями, эти вероятности в сообщении каждой группы примерно вдвое меньше начальных. Поэтому сообщение х_i, что послеk разбивок останется единственным в своей группе будет примерно равно Р(х_i)=1/2^k, откудаk=-log₂P(x_i). Но число знаков в кодовой комбинации (mi) равно числу разбивок, таким образом ее длинна равна:

Что отвечает условию оптимального кодирования. Пример:

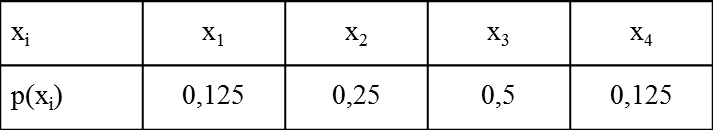
При решении практических задач не всегда удается разделить таблицу на две части с одинаковой вероятностью. Этот не достаток устраняется при использовании кода Хаффмана.

2. Код Хаффмана

Аналогично к коду Шеннона-Фано при использовании кода Хаффмана строится таблица в порядке уменьшения вероятности появления сообщений. Сообщения х_nи х_n-1соединяются в одну группу с вероятностью Р(х)=Р(х_n)+Р(х_n-1). Такое объединение повторяется до тех пор пока Р(х) не станет равно 1.

При кодировании кодом Хаффмана строится таблица

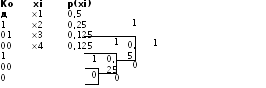
Отличие в кодировании в том, что в коде Шеннона-Фано формирование начинается со старшого (лівого) разряда. В коде Хаффмана кодове комбинации котируються начиння с младшего (правого) разряда.