Маслов А.В., Гордеев А.В., Батраков Ю.Г. - Геодезия

Из формулы (9.25) и графика (см. рис. 9.1, á) видно, что вероятность появления значения погрешности, подчиняющейся р˝авномерному закону распределения, во всем интервале (–à; +à)

одинакова. Это означает, что погрешности, подчиняющиеся р˝авномерному распределению, в больших рядах измерений в инте˝р-

âàëå (–à; +à) встречаются примерно одинаково часто независимо от их размера и знака. Три остальных свойства суммарных по˝- грешностей измерений остаются верными и для погрешносте˝й с равномерным распределением.

Случайными величинами являются и односторонне действую˝- щие погрешности. Характерное их отличие от погрешностей с˝ нормальным распределением заключается в том, что математ˝иче- ское ожидание ëюбой односторонне действующей погрешнос˝ти не равно нулю D = q ¹

При рассмотрении свойств какой-либо погрешности необход˝и- мо определить основной комплекс условий, при котором она ˝получена. Одна и та же погрешность, входящая в результаты изм˝ерения, может быть отнесена к различным видам погрешностей в˝ зависимости от рассматриваемого основного комплекса усло˝вий. Например, погрешность в измеренной длине линии из-за погр˝ешности в длине ленты будет постоянной (систематической) ил˝и случайной в зависимости от того, как измеряли или будут из˝мерять линию: одной и той же лентой или разными.

Раньше было отмечено (разд. 9.4), что необходимо различать стохастически зависимые и независимые случайные величи˝ны. Случайные погрешности, а следовательно, и измерения, их со˝держание, являются случайными величинами. Соответственно эт˝ому и измерения могут быть стохастически независимыми или за˝висимы между собой. Зависимость между двумя измерениями может˝

быть вызвана следующими причинами: погрешности измерени˝й имеют некоторые общие источники; на погрешность результа˝тов измерений наложены ограничительные условия (например, в ˝виде допусков для невязок).

В дальнейшем изложении будем считать, что измерения попар˝- но независимы.

9.6. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ ТОЧНОСТИ РЕЗУЛЬТАТОВ РАВНОТОЧНЫХ ИЗМЕРЕНИЙ

Точность измерений выражает степень близости результат˝а из-

мерения к действительному значению измеряемой величины˝.

Учитывая наличие случайных погрешностей в измерениях, эт˝а

близость различна для разных результатов. Поэтому точнос˝ть из-

мерений характеризуют некоторой средней величиной случ˝айной

погрешности.

281

В качестве теоретической характеристики точности измер˝ений

чаще всего берут среднее квадратическое отклонение

s = D (9.26)

где — случайная погрешность измерения.

Так как математическое ожидание случайной погрешности

равно нулю, т. е. = то ее дисперсия

∞

ãäå f(x) — плотность распределения случайной погрешности.

Среднее квадратическое отклонение постоянно (s = const) для неизменного основного комплекса условий измерений, поэт˝ому

оно характеризует условия измерений.

В связи с этим можно дать более широкое, чем раньше, опреде-˝

ление равноточности измерений: измерения называют равно˝то- чными, если сохраняется постоянство среднего квадратиче˝ского

отклонения s.

Величина s является теоретической характеристикой, и ее числовое значение неизвестно. Поэтому пользуются ее приближ˝енным значением — средней квадратической погрешностью, з˝наче-

ния которой находят по результатам измерений.

Допустим, что проведено ï равноточных измерений и при этом

получены случайные погрешности D1, D2, ..., Dï. Средняя квадрати- ческая погрешность или эмпирическое1 среднее квадратическое отклонение

Эта величина также случайная. По закону больших чисел для˝

случайных величин

Такие эмпирические характеристики, которые сходятся по в˝е-

роятности к соответствующим теоретическим характеристи˝кам, называют их состоятельными оценками.

1Слово «эмпирическое» часто опускают.

282

На основании формулы (9.30) можно принять, что при доста-

точно большом ï

Эмпирические характеристики, математические ожидания к˝о-

торых равны соответствующим теоретическим характеристи˝кам, называют их несмещенными оценками.

Таким образом, по формулам (9.30) и (9.33) квадрат средней квадратической погрешности ò2 является состоятельной и несме-

щенной оценкой дисперсии σ2.

Так как средняя квадратическая погрешность ò, вычисляемая

по формуле (9.29), определяет величину σ с некоторой погрешностью и является величиной случайной, для оценки точности ˝опре-

деления самой погрешности ò существует формула

Теоретической характеристикой точности измерений служи˝т

также предельная погрешность

ãäå τ — коэффициент, значение которого принимают таким, чтобы˝ была мала вероятность появления погрешности, по абсолютному значени˝ю больше предельной, т. е. чтобы была мала величина Ð(| | > τσ) = α.

Обычно для τ берут значения 3; 2,5 или 2. Этим значениям τ ñî-

ответствуют значения вероятностей α: 0,003, 0,012, 0,046.

Эти соотношения между значениями τ è α означают следующее: на каждую тысячу измерений число погрешностей, прево˝сходящих по абсолютному значению предельную ïð = 3σ, 2,5σ, 2σ, в среднем приблизительно равно соответственно 3, 12, 46.

Так как точное значение величины σ неизвестно, то вместо σ в формуле (9.35) берут ее приближенное значение ò, получаемое по

Иногда о точности измерений судят не по значению средней квадратической или предельной погрешности, а по значению˝ их

отношения к измеренной величине. Отношение погрешности к˝

283

измеренной величине называют относительной погрешностью

(средней квадратической, предельной).

П р и м е р. Угол, точное значение которого a = 34°15¢48², измерен шесть раз. Вычислить среднюю квадратическую и предельную погрешно˝сти измерения угла. Полученные результаты измерений и вычислений приведены˝ в таблице 9.2.

9.2. Оценка точности результатов измерений по случайным пог˝решностям

[D2] = 612

9.7. СРЕДНЯЯ КВАДРАТИЧЕСКАЯ ПОГРЕШНОСТЬ ФУНКЦИИ ИЗМЕРЕННЫХ ВЕЛИЧИН

Если известны средние квадратические погрешности каких˝- либо величин, то можно по ним определить среднюю квадрати˝- ческую погрешность любой функции этих величин. Например,

зная средние квадратические погрешности òs è òν соответственно

горизонтального проложения s и угла наклона ν линии, можно найти среднюю квадратическую погрешность превышения, оп˝ре-

деляемого по формуле h = s tg ν.

Задачи по оценке точности таких функций решают, используя˝

готовую формулу, которая выводится на основании положени˝й

теории вероятностей.

Для оценки точности функции общего вида

где s — дисперсия функции; s — дисперсии измеренных величин.

На практике дисперсии заменяют квадратами средних квадр˝а- тических погрешностей, полученных по большому числу резу˝льтатов измерений, поэтому вместо формулы (9.38) можно записать˝

284

ãäå k1, k2, …, kn, c — постоянные величины,

то частные производные этой функции равны коэффициентам˝ при переменных xi, ∂f/∂xi = ki.

Поэтому для линейной функции (9.40) формула по оценке точ-

ности имеет вид

квадратической погрешности

Функция общего вида

Линейные функции

=

В случае равноточных измерений, когда ò1 = ò2 = … = òï = ò, для функции (9.43)

Все приведенные формулы для средних квадратических погрешностей функций, кроме формулы (9.42), можно получить следующим образом.

Рассмотрим функции è = kx + c è U = ka + c. Вычтя из первого равенства второе, получим è = k x. Ïðè ï измерениях получим ряд таких равенств. Возведя каждое из них в квадрат, затем сложив˝ полу-

ченные результаты и разделив на ï, будем иметь [ u2]/n = k2[ x2]/n

или на основании формулы (9.29) получим выражение (9.42).

1Функцию называют линейной, если все ее члены, кроме свободного, первой степени относительно переменных.

285

Приведем примеры решения задач, где используют формулы

(9.39)…(9.44).

З а д а ч а 1. При определении расстояния по нитяному дальномеру польз˝уются формулой (2.27) s = Kl + c.

Считая, что Ê = 100 è ñ — точные значения величин, а l определено со средней квадратической погрешностью ò1 = 5 мм, надо найти среднюю квадратическую погрешность расстояния ms.

Согласно формуле (9.42)

ms = Kml = 100 · 0,005 = 0,5 ì.

З а д а ч а 2. Углы треугольника b1 è b2 измерены с точностью, характеризуемой погрешностями β = ¢ è β = ¢ Чему равна средняя квадратическая погрешность третьего угла треугольника, вычисленного по формул˝еb3 = 180° – b1 – b2?

З а д а ч а 3. Средняя квадратическая погрешность измерения каждого у˝гла треугольника равна 10². Чему равна средняя квадратическая погрешность суммы углов треугольника?

З а д а ч а 4. Вывести формулу для вычисления средней квадратической п˝о- грешности длины линии, измеренной лентой, через длину это˝й линии.

Допустим, что при помощи мерной ленты длиной l необходимо отложить отрезок линии длиной s, равной целому числу лент ï, ò. å. S = nl. В результате последовательного откладывания длины ленты на местности полу˝чим отрезок

s = l1 + l2 + … + ln.

Так как измерения равноточны, то средняя квадратическая п˝огрешность от-

кладывания отрезка s согласно формуле (9.44) будет = 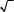ãäå ò — средняя квадратическая погрешность одного откладывания ленты. П˝риближенноï = s/l,

поэтому = 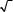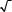Введя обозначение = m получим

Так как при измерении линии лентой погрешности накаплива˝ются так же, как и при откладывании отрезков, формула (9.45) справедлива и для˝ случая измерения линии длиной S¢1.

Величину ms называют коэффициентом случайного влияния линейных измерений. Приняв в формуле (9.45) s = 1 м, получим ms = ms.

Следовательно, коэффициент ms равен средней квадратической погрешности измерения линии длиной 1 м.

З а д а ч а 5. Вывести формулу для вычисления средней квадратической п˝о- грешности превышения по нивелирному ходу через длину ход˝аL.

Превышение h по всему ходу геометрического нивелирования равно сумме превышений h1, h2, …, hn, полученных на каждой станции, т. е. h = h1 +

+ h2 + … + hn.

Считая все превышения равноточными, согласно формуле (9.44) м˝ожно напи-

1Если измеряют отрезок длиной S = nl, то нетрудно видеть, что результат измерения будет s = 2S – (l1 + l2 + … + ln), на основании чего получают формулу (9.45).

286

Òàê êàê ï = L/d (ãäå L — длина хода, d — среднее значение суммы расстояний

ризуемой величинами òà è mb. Найти среднюю квадратическую погрешность площади прямоугольника.

Площадь прямоугольника Ð = ab.

Для оценки точности этой площади применим формулу (9.39), кот˝орая для данной задачи будет иметь вид

= ∂ ∂ + ∂ ∂

Подставив в эту формулу значения частных производных ∂Ð/∂à = b, ∂Ð/∂b = à, получим = +

9.8. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ РАВНОТОЧНЫХ ИЗМЕРЕНИЙ ОДНОЙ И ТОЙ ЖЕ ВЕЛИЧИНЫ. СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ ЗНАЧЕНИЕ И ЕГО СВОЙСТВА

Если получен ряд результатов равноточных измерений одно˝й и

той же величины, то проводят их математическую обработку,˝ при которой вычисляют: среднее арифметическое значение изме˝рен-

ной величины (как наиболее надежное); среднюю квадратичес˝кую погрешность одного измерения; среднюю квадратическую по˝- грешность среднего арифметического.

Среднее арифметическое значение из результатов равното˝чных измерений l1, l2, …, ln, которое также называют арифметическим средним, определяют по формуле

Для упрощения вычисления среднего арифметического обыч˝но вводят приближенное значение измеряемой величины l0.

Выбрав приближенное значение, вычисляют отклонения

εi = li – l0 (i = 1, 2, …, n).

Приближенное значение выбирают с таким расчетом, чтобы

отклонения εi были малы. Часто за l0 принимают наименьшее из li

или же округленный результат измерения, полученный путем˝ от-

брасывания варьирующей части результатов.

287

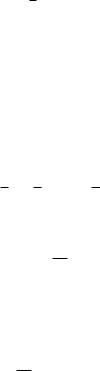
Из предыдущего равенства имеем li = l0 + εi (i = 1, 2, …, n).

Подставив это выражение в формулу (9.47), после некоторых преобразований получим

По этому равенству вычисляют среднее арифметическое чер˝ез

приближенное значение.

Среднее арифметическое из результатов равноточных изме˝рений одной и той же величины à обладает следующими свойства-

ìè:

при большом числе измерений оно приближается по вероятно˝-

сти к точному значению измеренной величины à, ò. å.

его математическое ожидание равно точному значению изме˝- ренной величины, т. е.

Эти свойства среднего арифметического, полученного по ре˝- зультатам измерений величины à, показывают, что оно является

состоятельной и несмещенной оценкой этой величины.

9.9. СРЕДНЯЯ КВАДРАТИЧЕСКАЯ ПОГРЕШНОСТЬ СРЕДНЕГО АРИФМЕТИЧЕСКОГО

Напишем выражение (9.47) в виде

=+ + +

Согласно формуле (9.41) для линейной функции

= = å

=

Так как имеются в виду равноточные измерения, то

ò1 = ò2 = … = òï = ò.

Следовательно,

==

288

откуда

т. е. средняя квадратическая погрешность Ì среднего арифмети-

ческого в 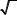раз меньше средней квадратической погрешности ò

одного измерения.

З а д а ч а. Из опыта установлено, что средняя квадратическая погрешност˝ь угла, измеренного одним приемом теодолитом Т30, равна 0,5′. Чему равна средняя квадратическая погрешность среднего арифметическог˝о из четырех приемов?

9.10.ПОПРАВКИ РАВНОТОЧНЫХ ИЗМЕРЕНИЙ ОДНОЙ

ÈТОЙ ЖЕ ВЕЛИЧИНЫ И ИХ СВОЙСТВА

Если имеется ряд равноточных измерений l1, l2, …, ln одной и той же величины и из результатов измерений получено средн˝ее арифметическое значение, то поправкой называют разность˝ меж-

ду средним арифметическим и результатом измерения, т. е.

Укажем на два свойства поправок равноточных измерений од˝- ной и той же величины:

Чтобы доказать первое свойство, просуммируем все равенства (9.52) с индексом i îò 1 äî ï и получим

Подставим в это равенство вместо L его выражение [l]/n. Тогда

[υ] = n[l]/n – [l] = 0.

Это свойство поправок используют для контроля правильно˝сти вычисления L è υi (i = 1, 2, …, ï).

Если значение L получено с округлением величины частного [l]/n, òî

ãäå ω — погрешность округления.

289

В этом случае равенство (9.53) точно выполняться не будет, а вм˝есто него должно выполняться соотношение [υ] = ïω, которое получается, если равенство (9.55) подставить выражение (9.56).

Òàê êàê |ω| ≤ 0,5 единицы последнего знака L, то должно выполняться условие |[υ]| ≤ 0,5ï единиц того же разряда. Все контроли остаются без изменения и при вычислении L через l0.

Смысл второго свойства ([υ2] = min) заключается в том, что сумма квадратов отклонений (поправок) результатов измерений от среднего˝ арифметического всегда меньше, чем от любого другого числа. Чтобы убедиться в с˝праведливости этого, возьмем функцию z = [υ′2] = [(x – l)2], в которой õ — переменная величина, а li (i = 1, 2, …, ï) — результаты измерений, и найдем ее минимум.

Для этого определим

dz/dx = 2(x – l1) + 2(x – l2) + … + 2(x – ln).

Приравняв эту производную к нулю и решив полученное равен˝ство относительно õ, найдем x = [l]/n. Следовательно,

Легко проверить, что при этом значении õ величина z будет иметь минимум,

ò.å. [υ2] = min.

9.11.ОПРЕДЕЛЕНИЕ СРЕДНИХ КВАДРАТИЧЕСКИХ ПОГРЕШНОСТЕЙ ОДНОГО ИЗМЕРЕНИЯ

ÈСРЕДНЕГО АРИФМЕТИЧЕСКОГО ПО ПОПРАВКАМ

ÊРЕЗУЛЬТАТАМ ИЗМЕРЕНИЙ

Пусть произведено ï равноточных измерений одной и той же величины, точное значение которой à неизвестно. В этом случае

точность результатов измерений l1, l2, …, ln оценивают по поправкам к ним.

В теории погрешностей измерений требуется, чтобы характе˝-

ристика точности ò2 была состоятельной и несмещенной оценкой дисперсии σ2. Этим условиям удовлетворяет характеристика

ò2 = [υ2]/(ï – 1).

Из этого равенства следует

Значения ò, полученные по формулам (9.29) и (9.57), будут

различаться между собой. Но так как по вероятности (при ï → ∞) они сходятся к σ, то при увеличении числа измерений они будут сближаться и между собой.

Средняя квадратическая погрешность ò, вычисляемая по фор-

муле (9.57), дает значение σ с некоторой погрешностью и является величиной случайной. Для оценки точности самой погрешнос˝ти ò существует приближенная формула

290