
Маслов А.В., Гордеев А.В., Батраков Ю.Г. - Геодезия
.pdf
Можно использовать более простой контроль |[pυ]| ≤ 0,5[p] единицы последнего знака Lâ.
Второе свойство поправок, соответствующих случаю неравн˝оточных измерений одной и той же величины, условно выражают в виде равенс˝тва p[υ2] = min.
Доказательство этого свойства аналогично приведенному ˝для случая равноточ- ных измерений.
9.19.ОЦЕНКА ТОЧНОСТИ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ
ÈСРЕДНЕГО ВЕСОВОГО ПО ПОПРАВКАМ
Если имеется ряд неравноточных измерений l1, l2, …, ln одной и
той же величины, для которых известны веса ð1, ð2, …, ðï, то точ- ность можно оценить по поправкам.
Âматематической статистике доказывается, что несмещенн˝ой
èсостоятельной оценкой σ является характеристика
μ2 = [pυ2]/(ï – 1). |
(9.96) |
Из равенства (9.96) следует, что
μ = |
υ |
(9.97) |
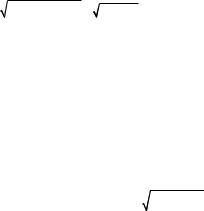
По этой формуле определяют среднюю квадратическую погрешность единицы веса через поправки. Значение μ, вычисляе-
мое по формуле (9.97), будет несколько отличаться от значения˝μ,
получаемого по формуле (9.86), но при неограниченном увеличе-˝ нии ï они будут сближаться между собой.
Подставив выражение (9.97) в формулу (9.93), найдем выражение средней квадратической погрешности среднего весово˝го через
поправки
= |
υ |
(9.98) |
Для контроля вычисления [pυ2] умножим равенства υi = Lâ – li
íà piυi (i = 1, 2, …, ï) и, просуммировав новые равенства по пере-
менному индексу i îò 1 äî ï, получим [pυ2] = Lâ[pυ] – [pυl]. Учитывая свойство поправок, что [pυ] = 0, будем иметь
[pυ2] = –[pυl]. |
(9.99) |
Заменив в этом равенстве каждое li его выражением li = l0 + εi,
получим [pυ2] = –[pυ]l0 – [pυε].
Учитывая свойство поправок, что [pυ] = 0, будем иметь
[pυ2] = –[pυε]. |
(9.100) |
Равенства (9.99) и (9.100) могут быть использованы для контро-
ля правильности вычислений Lâ è υi.
301
Иногда для контроля используют несколько иные равенства˝,
например
[pυ2] = [pε2] – [pε]2/[p].
Åñëè Lâ было получено с округлением, что для строгого контроля может быть использовано равенство
[pu2] = –[pue] + (Lâ – l0)[pu]
или для приближенного контроля — неравенство
|[pu2] + [pue]| £ 0,5|[pe]| единицы последнего знака Lâ.
Çа д а ч а. Обработать результаты ряда неравноточных измерений (таб˝л. 9.5),
ò.е. найти среднее весовое и его среднюю квадратическую п˝огрешность.
9.5.Оценка точности результатов неравноточных измерений
Номер |
Измеренное |
|
Âåñ |
|
ε |
ðε |
υ |
pυ |
pυ2 |
pυε |
|
|
èçìå- |
значение |
m |
= |
|
|
|
||||||
рения |
óãëà l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
134°15¢18² |
5² |
4 |
|
+8 |
+32² |
–3,4² |
–13,6² |
46 |
–109 |
|
|
2 |
26 |
10 |
1 |
|
+16 |
+16 |
–11,4 |
–11,4 |
130 |
–182 |
|
|
3 |
13 |
2 |
25 |
|
+3 |
+75 |
+1,6 |
+40,0 |
64 |
+120 |
|
|
4 |
11 |
5 |
4 |
|
+1 |
+4 |
+3,6 |
+14,4 |
52 |
+14 |
|
|
5 |
22 |
5 |
4 |
|
+12 |
+48 |
–7,4 |
–29,6 |
219 |
–355 |
|
|
l0 = 134°15¢10² |
|
38 |
|
|
+175² |
|
–0,2² |
511 |
–512 |
|
||
â= 134°15¢10² + 175/38 = 134°15¢14,6²; w = –0,0053².
Êî í ò ð î ë ü: [pu] = [p]w = –0,2²; [pu2] = –[pue] + (Lâ – l0)[pu] = 512 + 4,6(–0,2) =
=511.
= |
u |
= |
= ¢¢ » ¢¢ |
9.20. СРЕДНЯЯ КВАДРАТИЧЕСКАЯ ПОГРЕШНОСТЬ ЕДИНИЦЫ ВЕСА, ОПРЕДЕЛЯЕМАЯ ПО РАЗНОСТЯМ ДВОЙНЫХ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ
Предположим, что имеется ряд двойных неравноточных измерений li, ′ каждое с весом ði (i = 1, 2, …, ï). Составим разности
=′ (i = 1, 2, …, ï).
Как и в случае равноточных измерений, эти разности равны
погрешностям самих разностей. Поэтому согласно формуле (˝9.86)
|
μ = |
(9.101) |
Íî = |
′ — функция двух равноточных измерений. При- |
|
менив к этой формуле формулу (9.81), получим |
= |
|
|
||
302

Подставив выражение веса |
в формулу (9.101), окончатель- |
но найдем |
|
m = |
(9.102) |
По формуле (9.102) определяют среднюю квадратическую погрешность единицы веса, если в разностях нет систематичес˝ких
погрешностей. В случае наличия систематических погрешно˝стей последние предварительно исключают из разностей (см. раз˝д.
9.21).
9.21. ОЦЕНКА ТОЧНОСТИ ЛИНЕЙНЫХ ИЗМЕРЕНИЙ ПО РАЗНОСТЯМ ДВОЙНЫХ ИЗМЕРЕНИЙ ЛИНИЙ
Пусть имеется ряд двойных измерений линий лентой si, ¢ (i = 1, 2, …, ï).
Если в разностях нет систематических погрешностей, то сре˝д- няя квадратическая погрешность единицы веса может быть о˝пре-
делена по формуле (9.102), в которой = ¢ На основании формулы (9.73) веса линейных измерений опре-
деляют как величины, обратно пропорциональные длинам лин˝ий,
ò. å. ði = 1/si.
Подставив это значение в формулу (9.102), получим
m = |
é |
ù |
(9.103) |
|
ê |
|
ú |
||
|
||||
|
ê |
ú |
|
|
|
ë |
û |
|
|
На основании выражения (9.87) можно написать контрольное равенство
m = |
(9.104) |
Если в разностях di имеются систематические погрешности qi
(i = 1, 2, …, ï), то поступают следующим образом. Полагают, что
систематические погрешности измерения линий пропорцион˝альны их длинам, т. е.
qi = qsi, |
(9.105) |
ãäå θ — коэффициент пропорциональности, а вес ði = 1/si.
|
Вычисляют приближенное значение q по формуле |
|
|
q = [d]/[s]. |
(9.106) |
|
Формулу (9.106) можно получить так. Представим разность в виде˝ = |
+ θ |
ãäå |
è θi — соответственно случайная и систематическая составля˝ющие. Тогда |
|
303

[d] = [ d] + [θ], à òàê êàê θi = θsi, òî [d] = [ d] + θ[s]. Разделим полученное равенство на [s]. Получим [d]/[s] = [ d]/[s] + θ. Случайные погрешности в сумме в зна-
чительной мере погашаются. Поэтому при большом значении [˝s] первый член правой части последнего равенства при наличии системати˝ческих погрешностей θi будет мал по сравнению с θ и его можно отбросить. Тогда получим формулу (9.106).
Получив θ, находят систематические погрешности θi = θsi,
∂i = di – θi (i = 1, 2, …, ï). |
(9.107) |
Среднюю квадратическую погрешность единицы веса в этом
случае вычисляют по формуле
μ = |
(9.108) |
Åñëè si выражено числом метров, то по формулам (9.103),
(9.108) можно получить значения коэффициента случайного влия˝-
ния линейных измерений, т. е. μ = μs.
Величину θ называют коэффициентом остаточного системати- ческого влияния линейных измерений.
Для контроля вычислений θi, ∂i è [d2/s] просуммируем равен-
ñòâà θi = θsi (i = 1, 2, …, ï) по переменному индексу i îò 1 äî ï и получим [θ] = θ[s]. Заменив в этом равенстве величину θ согласно
формуле (9.106), найдем [θ] = [d].
Сложив равенства вида (9.107), получим [∂] = [d] – [θ]. Отсюда,
имея в виду предыдущее равенство, [∂] = 0. Контрольное равенство [∂/s] = [d2/s] – [d]2/[s].
Если при вычислении θ как частного был отброшен остаток r, ò. å. θ получено из равенства θ = ([d] – r)/[s], òî [θ] = [d] – r, [∂] = r.
Оценка точности по разностям двойных измерений часто не
дает полного представления о точности проведенных измер˝ений.
Так, при измерении линий одной и той же лентой дважды имею-
щаяся в результате измерений погрешность из-за неточного˝ опре-
деления длины ленты при ее компарировании в разностях дво˝й-
ных измерений исключается.
То же самое будет с погрешностями в углах, если эти погрешности возникают из-за неточного центрирования теодолита˝, когда каждый угол измеряют дважды при одной и той же установке п˝рибора.
Можно еще указать примеры, когда влияние некоторых источ-˝
ников погрешностей в разностях исключается в значительн˝ой сте-
пени, например влияние температуры, рельефа местности при˝ измерении линий или влияние рефракции при измерении углов.
Известны случаи, когда средние квадратические погрешнос˝ти
измерений линий, полученные по разностям двойных измерен˝ий, оказались в три-четыре раза меньшими по сравнению с дейст˝ви-
тельными.
304
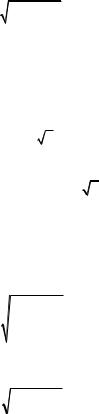
9.22.ОЦЕНКА ТОЧНОСТИ ИЗМЕРЕНИЙ УГЛОВ
ÈПРЕВЫШЕНИЙ ПО НЕВЯЗКАМ В ПОЛИГОНАХ И ХОДАХ
Если измерения должны удовлетворять какому-либо геометр˝и- ческому условию (например, сумма внутренних углов треуго˝льни-
ка должна быть равна 180°), то точность измерений можно опред˝е-
лить по невязкам, получающимся в результате погрешностей˝ измерений. Для примера определения точности измерений по не˝-
вязкам приведем решения двух задач.
1. В результате измерений углов в N полигонах (ходах) с числом
углов ï1, ï2, …, ïN получены невязки f1, f2, …, fN. Определить среднюю квадратическую погрешность измерения одного угла.
Полученные невязки являются погрешностями сумм углов в каждом полигоне (ходе), поэтому для оценки точности измере˝ний
можно воспользоваться формулой (9.86). Заменив в ней погрешности Di íà fi, à ï на число полигонов (ходов) N, получим
μ = |
β |
(9.109) |
ãäå ð1, ð2, …, ðN — веса сумм углов в полигонах.
Вес суммы измеренных углов найдем по формуле
= |
Σβ |
(9.110) |
Средняя квадратическая погрешность суммы углов равна
Σβ =
ãäå ò — средняя квадратическая погрешность измерения одного˝ угла.
Выразив òΣβ в формуле (9.110) через |
получим ð = k/nm2. |
Примем вес измерения одного угла равным единице, т. е. k/m2 = 1,
тогда k = m2.
При этом значении k формула для весов сумм углов примет вид ð = 1/ï. Подставив это выражение веса в формулу (9.110) и имея в виду, что в этом случае величина m будет равна средней квадрати- ческой погрешности измерения одного угла, получим
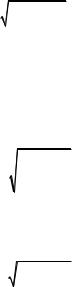
= |
é |
β |
ù |
|
ê |
|
ú |
(9.111) |
|
|
||||
|
ê |
|
ú |
|
|
ë |
|
û |
|
На основании выражения (9.87) можно применить конт-
рольную формулу
= |
é |
β |
ù |
(9.112) |
|
ë |
|
û |
|
305
В частном случае, когда невязки f1, f2, …, fN относятся к суммам
углов в треугольниках, предыдущая формула примет вид
=é ù (9.113)
ë β û
2.Имеются невязки f1, f2, …, fN в суммах превышений нивелир-
ных полигонов (ходов), периметры которых L1, L2, …, LN. Найти среднюю квадратическую погрешность превышения по ходу д˝ли-
íîé 1 êì.
Невязки f1, f2, …, fN — это погрешности соответствующих сумм
превышений, веса которых ði = 1/Li. Воспользовавшись формулой (9.86), найдем
= |
é |
ù |
(9.114) |
|
ê |
|
ú |
||
|
||||
|
ê |
ú |
|
|
|
ë |
û |
|
|
ãäå Li â êì.
На основании формулы (9.87) можно написать контрольное равенство
= |
é |
ù |
(9.115) |
|
ë |
û |
|
9.23. НАЗНАЧЕНИЕ ТЕХНИЧЕСКИХ ДОПУСКОВ ДЛЯ РАСХОЖДЕНИЙ И НЕВЯЗОК В ГЕОДЕЗИЧЕСКИХ
ИЗМЕРЕНИЯХ
Одной из важных прикладных задач теории погрешностей из-
мерений является разработка методов вычисления допусти˝мых не-
вязок и расхождений при проведении различных геодезичес˝ких
работ.
Основанием для расчета допусков служит то, что любая невя˝зка (расхождение) является погрешностью самой невязки (расхо˝ждения). В самом деле, теоретическое значение любой невязки ра˝вно нулю, так как оно должно быть вычислено по точным значения˝м измеренных величин. Например, угловую невязку теодолитно˝го полигона получают по формуле (3.1):
fβ = Σbïð – Σbò.
Если нужно получить теоретическое значение невязки, то ве˝- личину Σbïð необходимо вычислять по точным значениям углов. Тогда Σbïð = Σbò, так как практическая сумма безошибочна, и,
следовательно, β =
306
В то же время согласно формуле (1.25) погрешность — раз-
ность между результатом измерения и его точным значением˝, что приводит к соотношению f = f – fò = f, ãäå f — погрешность невязки.
Из последнего соотношения следует, что предельно возможн˝ое при данных условиях значение невязки, которое обычно назы˝вают допустимой невязкой, совпадает с предельной погрешность˝ю этой невязки, т. е. верно соотношение fäîï = fïðåä.
Вычисление предельной погрешности fïðåä может быть осуще-
ствлено, если известно значение средней квадратической п˝огрешности mf невязки, тогда согласно формуле (9.36) fïðåä = τmf, где коэффициент τ при нормальном распределении погрешностей из-
мерений может принимать значения 2, 2,5 и 3 в зависимости от выбранной вероятности.
При любых значениях τ существует определенная вероятность, что некоторое число нормальных измерений может быть приз˝на-
но некачественным. При τ = 2 таких измерений больше, чем при других значениях этого коэффициента, но в этом случае жес˝тко отбраковывают уклоняющиеся измерения. Так, если оказалос˝ь,
÷òî mf = 1′, òî ïðè τ = 2 любая невязка, большая чем fïðåä = 2 · 1′ = = 2′, признается недопустимой и такие измерения бракуют. При
τ = 3 в этих же условиях бракуют измерения, если невязки буду˝т превышать значение fïðåä = 3′.
Значение mf обычно вычисляют по известным правилам оцен-
ки точности функций в зависимости от вида геодезических д˝ействий (см. разд. 9.7).
Подобные рассуждения можно применять для вычисления до-
пустимых расхождений между двумя измерениями одной и той˝ же величины l1 è l2 со средними квадратическими погрешностями со-
ответственно ò1 è ò2. Требуется определить допустимое расхождение dïðåä между полученными результатами измерений. Естественно считать, что допустимое расхождение — предельн˝о воз-
можное. Точное значение расхождения будет равно нулю, а пр˝е-
дельное расхождение — его предельной погрешности, т. е. däîï =
= dïðåä = dïðåä. Считая, что dïðåä = τmd, получаем däîï = τmd.
Íî d = l1 – l2. Тогда согласно формуле (9.44) при ò1 = ò2 = ò
=τ 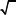
Çа д а ч а 1. Вычислить допустимую угловую невязку в теодолитном ходе˝,
если каждый угол измерен со средней квадратической погре˝шностьюòβ, число углов в ходе ï, а погрешностями исходных дирекционных углов можно прене˝б- речь ввиду их малости.
Для левых углов будем иметь
fβ = Σβïð – Σβò = β1 + β2 + ... + βï – (αê + ï · 180° – αí).
На основании формулы (9.44) получим β = β 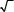
307
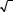
Тогда допустимая угловая невязка может быть вычислена по˝ формуле
β= t β 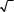
Это наиболее общее представление о допустимой угловой не˝вязке. При измерении углов теодолитом Т30 òβ = 0,5¢; принимая t = 2, получим следующее выражение для допустимой угловой невязки:
β= ¢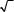
Если углы измеряют в триангуляции второго разряда со сред˝ней квадратической погрешностью òβ = 10², то допустимая невязка в треугольнике при t = 2,5
β = |
¢¢ = |
¢¢ |
В инструкциях эту величину обычно округляют до 45².
З а д а ч а 2. Определить допустимое расхождение между двумя измерени˝ями лентой линии длиной 250 м, если коэффициент случайного влия˝нияms = 0,004 ì.
Для решения задачи сравнивают два равноточных измерения˝s1 è s2. Средняя квадратическая погрешность каждого из них может быть пол˝учена по формуле
(9.45): = m 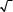
Тогда допустимое расхождение, полученное по формуле (9.44), о˝кажется равным
= tm 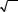
Для рассматриваемого случая при t = 2,5 будем иметь
= =
=
Контрольные вопросы и задания
1. Что называют погрешностью измерения? 2. Назовите погрешно˝сти по характеру их действия и источнику происхождения. 3. Дайте опр˝еделение теории вероятности. 4. Какие свойства случайных погрешностей вы з˝наете? 5. Каковы числовые характеристики точности результатов равноточн˝ых измерений? 6. Напишите и объясните формулы оценки точности функций общег˝о вида и линейных функций. 7. Как обрабатывают результаты равноточных измер˝ений одного и того же значения? 8. Как определяют неравноточные измерения, вес˝а измерений и их свойства? 9. Дайте определение весов функций измеренных ве˝личин и напишите для них формулы весов. 10. Объясните формулу средней квадрат˝ической погрешности единицы веса. 11. Объясните формулу средней квадратич˝еской погрешности среднего весового. 12. Как оценивают точность линейных и˝змерений? 13. Напишите формулы и объясните процедуру оценки точности угл˝ов и превышений по невязкам в полигонах и ходах.
308

à ë à â à 10
ОБЩИЕ СВЕДЕНИЯ О ПОСТРОЕНИИ ГЕОДЕЗИЧЕСКОЙ СЕТИ ПРИ СЪЕМКЕ НА БОЛЬШОЙ ТЕРРИТОРИИ
∙
10.1. ПОНЯТИЕ О ГЕОДЕЗИЧЕСКОЙ СЕТИ
При проведении различных народнохозяйственных, в том чис˝- ле и землеустроительных, мероприятий на большой территор˝ии
необходимы топографические карты и планы, составленные н˝а основе сети геодезических пунктов, плановое положение ко˝торых
на земной поверхности определено в единой системе коорди˝нат, а
высотное — в единой системе высот. При этом геодезические сети могут быть плановыми, высотными или одновременно плановы˝ми и высотными.
Сеть геодезических пунктов располагают на местности сог˝ласно составленному для нее проекту. Пункты сети закрепляют ˝осо-
быми знаками.
Построенная на большой территории в единой системе координат и высот геодезическая сеть дает возможность правил˝ьно
организовать работу по съемке местности. При наличии тако˝й сети съемку можно проводить в разных местах, что не вызове˝т затруднения при составлении общего плана или карты. Использ˝ова-
ние сети геодезических пунктов приводит к более равномер˝ному
распределению по территории влияния погрешностей измер˝ений
и обеспечивает контроль выполняемых геодезических рабо˝т. Геодезические сети строят по принципу перехода от общего˝ к
частному, т. е. вначале на большой территории строят редку˝ю сеть пунктов с очень высокой точностью, а затем эту сеть послед˝овательно по ступеням сгущают пунктами, которые строят на ка˝ждой
ступени с меньшей точностью. Таких ступеней сгущения быва˝ет
несколько. Сгущают геодезическую сеть с таким расчетом, ч˝тобы
в результате получилась сеть пунктов такой плотности (гу˝стоты) и
точности, чтобы они могли служить непосредственной опоро˝й для
предстоящей съемки.
Плановые геодезические сети строят в основном методами т˝риангуляции, полигонометрии и трилатерации. Иногда эти мето˝ды
сочетают.
Метод триангуляции состоит в строительстве сети треугольников, в которых измеряют все углы и как минимум две стороны на разных концах сети (вторую сторону измеряют для контроля˝ из-
мерения первой стороны и установления качества всей сети˝). По
309
длине одной из сторон и углам треугольников определяют ст˝оро-
ны всех треугольников сети. Зная дирекционный угол одной ˝из сторон сети и координаты одного из пунктов, можно вычисли˝ть координаты всех пунктов. В этом заключается сущность мето˝да триангуляции. На практике применение метода триангуляци˝и бо-
лее сложно.
Метод полигонометрии заключается в построении сети ходов, в
которых измеряют все углы и стороны. Полигонометрические˝ ходы отличаются от теодолитных более высокой точностью и˝зме-
рений. Этот метод обычно применяют в закрытой местности. В˝не-
дрение в производство электромагнитных дальномеров дел˝ает целесообразным применение полигонометрии и в открытой мес˝тности.
Метод трилатерации состоит в построении сети треугольников,
в которых измеряют все стороны. В некоторых случаях созда˝ют линейно-угловые сети, представляющие собой сети треуголь˝ни-
ков, в которых измерены стороны и углы (все или в необходим˝ом их сочетании).
Плановые геодезические сети делятся на государственную˝ геодезическую сеть, разрядные сети сгущения 1-го и 2-го разрядо˝в,
съемочное обоснование — съемочную сеть и отдельные пун˝кты.
10.2. ГОСУДАРСТВЕННАЯ ГЕОДЕЗИЧЕСКАЯ СЕТЬ
Государственная геодезическая сеть представляет собой ˝совокупность геодезических пунктов, равномерно распределен˝ных на
территории всей страны и закрепленных на местности центр˝ами, обеспечивающими сохранность и устойчивость этих пункто˝в в те-
чение длительного времени.
Согласно Основным положениям о построении государствен˝- ной геодезической сети СССР, 1954 г., ее подразделяют: на триан˝- гуляцию, полигонометрию и трилатерацию 1, 2, 3 и 4-го классов; нивелирные сети I, II, III и IV классов.
Государственную геодезическую сеть создают по принципу от общего к частному (от высшего класса к низшему). Это означа- ет, что сначала строят достаточно редкую сеть пунктов, опр˝еде-
ленных с очень высокой точностью. Затем эту сеть сгущают п˝унк-
тами, определяемыми с менее высокой точностью.
Рассмотрим схему построения плановой государственной г˝ео-
дезической сети методом триангуляции, так как в основном ˝этим методом построена существующая сеть.
В первую очередь строят триангуляцию 1-го класса в виде рядов треугольников (близких к равносторонним), которые рас˝полагают по возможности вдоль меридианов и параллелей (рис. 10.˝1). Длины сторон треугольников, как правило, не менее 20 км. Ряд˝ы треугольников образуют замкнутые полигоны периметром о˝коло
310
