Маслов А.В., Гордеев А.В., Батраков Ю.Г. - Геодезия

à ë à â à 9

ТЕОРИЯ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ

∙

9.1. СУЩНОСТЬ И ВИДЫ ИЗМЕРЕНИЙ

Измерение величины (длины линии, горизонтального, вертикального углов, превышения, площади и т. п.) — процесс срав˝нения этой величины с другой, однородной ей, принятой за един˝ицу

меры. В результате этого процесса находят число, равное от˝ноше-

нию измеряемой величины к единице меры, которому приписы-˝ вают наименование единицы меры и называют результатом измерения.

Существуют понятия: необходимые è избыточные измерения.

Если одна и та же величина измерена ï раз, то одно из измерений является необходимым, а остальные ï – 1 — избыточными.

Избыточные измерения используют для контроля правильно˝-

сти получаемых результатов измерений. Кроме того, они поз˝воляют определить более надежное значение искомой величины. П˝ри достаточном числе избыточных измерений можно судить о то˝чно-

сти произведенных измерений.

9.2. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ

Из практики измерений установлено, что при многократных измерениях одной и той же величины мы не получаем одинако˝вых

результатов, как бы тщательно их ни проводили.

Факт колебаний результатов измерений указывает на то, что˝

получаемые результаты не являются точным значением изме˝ряе-

мой величины, а несколько отклоняются от него.

Отклонение результата измерения величины от ее точного з˝на-

чения называют погрешностью измерения1. Это определение погрешности измерения можно написать в виде равенства (1.25):

= l – a,

где — погрешность измерения; l — результат измерения; à — точное значение величины.

1Определение погрешности по смыслу совпадает с определен˝ием невязки.

271

Из сказанного следует, что результаты измерений всегда со˝про-

вождаются погрешностями. Получить абсолютно точное знач˝ение величины невозможно.

Любая погрешность результата измерения — это следствие˝ действия многих факторов, каждый из которых порождает свою п˝о-

грешность. Погрешности, происходящие от отдельных фактор˝ов, называют элементарными. Таким образом, погрешность резул˝ьта-

та измерения является алгебраической суммой элементарн˝ых погрешностей. Все дальнейшее изложение относится как к сумм˝ар-

ным, так и к элементарным погрешностям.

Погрешности измерений разделяют по двумя признакам: характеру их действия и источнику происхождения.

По характеру действия различают погрешности: грубые, сист˝е-

матические и случайные. Грубыми называют погрешности, превы-

шающие по абсолютному значению некоторый установленный˝ для данных условий измерений предел. Они происходят в бол˝ь-

шинстве случаев от невнимательности исполнителя.

Для выявления грубых погрешностей проводят избыточные и˝з-

мерения тем же прибором или другим, но той же точности. Например, для контроля длину линии измеряют лентой дважды,

причем иногда первый раз измеряют 20-метровой, а второй — 24-метровой лентой. Результаты, содержащие грубые погрешно-

сти, бракуют и заменяют новыми, поэтому при дальнейшем изл˝о- жении будем считать, что результаты измерений свободны от˝ гру-

бых погрешностей.

Систематическими погрешностями называют такие, которые при многократных измерениях не изменяются, изменяются по˝ ка- кому-то определенному закону или, изменяясь случайным обр˝а-

зом, сохраняют знак. В соответствии с этим различают три ви˝да

систематических погрешностей: постоянные (в длине линии из-за

неточности компарирования ленты), переменные (в направлении при угловых измерениях вследствие изменения с течением в˝ремени фазы освещенности солнцем визирного цилиндра геодези˝ческого знака) и односторонне действующие (в длине линии из-за выхода ленты из створа измеряемой линии).

Переменные систематические погрешности часто являются функциями неслучайного аргумента (функциональные погре˝ш-

ности), но бывают и более сложной природы. Односторонне

действующие погрешности представляют собой четные функции

случайных величин. Функциональные изучают средствами эл˝е-

ментарной математики и анализа бесконечно малых величин˝, од-

носторонне действующие — средствами теории вероятностей и математической статистики.

Погрешности, не зависящие от результатов измерений и в по˝с- ледовательности появления которых нет никакой закономе˝рности, но в совокупности подчиняющиеся определенному вероят˝нос-

тному закону, называют случайными.

272

По источнику происхождения различают погрешности прибо˝-

ров, внешние и личные.

Погрешности приборов обусловлены несовершенством конструкций приборов или неточной их юстировкой. Например, погрешность в отсчете по горизонтальному кругу теодолита п˝ри на-

ведении зрительной трубы на предмет может быть вызвана ко˝ллимационной ошибкой.

Внешние погрешности происходят из-за влияния внешней среды, например погрешность в отсчете по нивелирной рейке из˝-за

влияния рефракции.

Личные погрешности вызваны особенностями наблюдателя. Например, замечено, что при работе с планиметром некоторые н˝а- блюдатели преувеличивают отсчет, а другие — преуменьша˝ют.

Некоторые систематические погрешности можно устранить ˝из

результатов измерений, применив соответствующие методы˝ измерений. Например, при нивелировании из середины исключаетс˝я

погрешность из-за непараллельности визирной оси и оси цил˝индрического уровня. Влияние же некоторых других систематич˝еских

погрешностей можно значительно ослабить, введя соответс˝твующие поправки. Методы борьбы с влиянием систематических по˝-

грешностей изучают в специальных дисциплинах, связанных˝ с проведением измерений.

При дальнейшем изложении теории погрешностей будем счи- тать, что результаты измерений свободны не только от грубых, но

и от систематических погрешностей. Лишь в отдельных случа˝ях

будет рассмотрена оценка точности результатов измерени˝й, которые содержат систематические погрешности.

9.3. ПРЕДМЕТ И ЗАДАЧИ ТЕОРИИ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ

Теория погрешностей измерений рассматривает классифика˝-

ции и свойства погрешностей измерений, методы получения п˝о

результатам измерения наиболее близкого результата к ее˝ точному

значению, а также получение числовых характеристик точно˝сти

измерений.

В соответствии с этим основными задачами теории погрешно˝с- тей измерений являются: определение по результатам измер˝ений их среднего значения; оценка точности результатов измере˝ний; оценка точности функций измеренных величин.

Излагаемые в теории погрешностей методы решения этих зад˝ач

дают возможность предварительно рассчитать точность пр˝едстоя-

щих геодезических измерений, что необходимо для правильн˝ой организации работ (выбора надлежащего прибора, соответст˝вующей методики измерения и т. п.). После проведения измерений˝

эти методы позволяют получить более точные значения изме˝ренных величин и оценить их точность.

273

9.4. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Математической основой теории случайных погрешностей и˝з- мерений являются теория вероятностей и математическая с˝тати-

стика.

Теория вероятностей — наука, изучающая закономерности массовых случайных явлений (событий), происходящих при неизм˝ен-

ном основном комплексе условий испытаний (наблюдений, из˝мерений) и обладающих статистической устойчивостью.

Случайным называют такое событие, осуществление которого заранее нельзя предвидеть (прогнозировать): оно может про˝изой-

ти, но может и не произойти.

Событие, которое при повторении опыта непременно должно

произойти, называют достоверным, событие же, которое заведомо не может произойти, — невозможным.

Случайные события, происходящие при неизменном основном˝

комплексе условий, в основном обладают определенной стат˝исти- ческой закономерностью, соответствующей данному компле˝ксу условий. В частности, эта закономерность проявляется в ус˝тойчи-

вости частости событий.

Частостью события называют отношение числа k появления события в ряду результатов испытания к числу всех членов этого

ðÿäà ï, ò. å.

Приведем пример, поясняющий понятие частости. Допустим,

что одно и то же превышение измерено 100 раз, при этом известн˝о

действительное значение превышения с высокой степенью т˝очности. На основании этого вычислены случайные погрешности и˝з-

мерений (считая, что грубых и систематических погрешност˝ей в

результатах измерений нет) и подсчитано число погрешност˝ей

каждого размера (табл. 9.1). Частости получены в результате д˝еле-

ния числа погрешностей определенного размера на число вс˝ех по-

грешностей в ряду.

9.1. Частости погрешностей в зависимости от их значений

274

Рассматривая несколько рядов результатов испытаний, про˝ве-

денных при одном и том же основном комплексе условий, можн˝о заметить, что при переходе от одного ряда к другому частости одного и того же события имеют некоторые колебания, но чем больше испытаний в каждом ряду, тем эти колебания меньше,

т. е. с увеличением числа испытаний в ряду колебания часто˝стей события затухают и значения частости, стабилизируясь, при˝бли-

жаются к некоторому числу. Это число называют вероятностью события, которая отражает существующую реальность — ст˝епень

возможности появления события при данном неизменном ком˝п-

лексе условий. Чаще всего вероятность обозначают буквой ð. Ввиду устойчивости частости при достаточном большом ï

По этой причине частость иногда называют эмпирической вероятностью.

Нетрудно определить, что частость и вероятность могут изм˝е-

няться от 0 до 1, т. е.

Очевидно, что частость и вероятность невозможного событи˝я

равны нулю, а достоверного события — единице.

Сумма частостей всех t событий какого-либо ряда результатов испытаний равна единице:

Такое же соотношение существует и для соответствующих ве˝-

роятностей

Рассмотрим еще одно важное для теории погрешностей измерений понятие случайной величины. Случайной называют переменную величину, появление какого-либо значения которой представляет собою случайное событие. Простейший пример˝ слу- чайной величины — частость событий. Другим примером слу˝чайной величины может служить погрешность измерений, провод˝и- мых при неизменном основном комплексе условий.

Различают прерывные (дискретные) è непрерывные случайные величины.

Если представить значения случайной величины как абсцис˝сы точек на оси, то в случае дискретной величины эти точки буд˝ут

275

отделены друг от друга, а в случае непрерывной величины он˝и

сплошь заполняют некоторый отрезок.

Случайную величину (совокупность всех ее значений) полно˝- стью характеризует закон ее распределения, представляющий собой выражение связи между значениями случайной величины и со˝от-

ветствующими им вероятностями.

Закон распределения случайной величины называют также з˝а-

коном распределения вероятностей, а чаще — распределен˝ием случайной величины. Закон распределения может быть выраж˝ен в

различной форме.

Распределение дискретной случайной величины Õ с конечным числом значений обычно представляют в виде таблицы распр˝еделения

ãäå õ1, õ2, ..., õi — все возможные значения случайной величины Õ, à ð1, ð2, ..., ði — соответствующие им вероятности.

Распределение непрерывной случайной величины задают фу˝н- кцией распределения

или плотностью распределения случайной величины Õ (плотностью вероятности)

ãäå F′ ′(x) — производная от F(x).

Правая часть равенства (9.8) обозначает вероятность того, чт˝о случайная величина Õ в результате испытания примет значение

меньше произвольного числа õ.

Для непрерывной случайной величины существует соотноше˝-

ние, аналогичное формуле (9.6),

∞

В теории погрешностей измерений необходимо различать ст˝о-

хастически (вероятностно) независимые и зависимые случа˝йные величины (в частности, случайные погрешности). Две случайн˝ые величины называют независимыми между собой, если изменен˝ие одной из них не влияет на распределение другой. В противно˝м

случае величины называют зависимыми.

Ч и с л о в ы е х а р а к т е р и с т и к и с л у ч а й н ы х в е л и ч и н. Для практических целей часто нет необходимости знать зак˝он рас-

пределения случайной величины, а достаточно иметь значен˝ия некоторых параметров этого закона (числовых характерист˝ик слу-

276

чайной величины). Такими характеристиками являются матем˝а-

тическое ожидание и дисперсия (или среднее квадратическо˝е отклонение).

Математическим ожиданием случайной величины Õ называют числоÕ, определяемое равенством

åñëè Õ — прерывная величина, заданная таблицей распределения˝,

èëè

∞

åñëè Õ — непрерывная величина с плотностью распределения f(x). Имеется связь между математическим ожиданием случайной˝

величины и средним арифметическим значением из результа˝тов ее наблюдений. Так, если произведено ï испытаний прерывной

случайной величины при неизменном основном комплексе ус˝ловий и получен ряд всех возможных ее значений õ1(k1),

õ2(k2), ..., õt(kt), то среднее арифметическое из них

Ранее уже было сказано, что при большом числе испытаний частость приближенно равна вероятности ≈ [см. формулу

(9.2)]. Заменив в последнем равенстве частости соответствующ˝и-

ми вероятностями, придем к определению математического о˝жи-

дания (9.11). Отсюда следует, что при достаточно большом числе˝

испытаний ï

Чем больше число испытаний ï, тем ближе среднее арифмети-

ческое значение к соответствующему математическому ожи˝данию.

Это свойство среднего арифметического является одним из˝ выра-

жений закона больших чисел, который в этом случае может бы˝ть записан в виде

ãäå Ð — обозначение вероятности; ε — сколь угодно малое положительное число.

277

ний случайной величины Õ, полученных в результате испытаний,

при неограниченном увеличении числа îпытов сходится по в˝еро-

ятности к математическому ожиданию

т. е. положительное значение квадратного корня из дисперс˝ии этой величины.

9.5. РАВНОТОЧНЫЕ ИЗМЕРЕНИЯ. СВОЙСТВА СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ

Если измеряют одну и ту же величину несколько раз или изме˝- ряют однородные величины1 при неизменном основном комплек-

се условий, т. е. одинаковыми по точности приборами, лицами˝ одинаковой квалификации, одним и тем же методом и при один˝а-

ковых внешних условиях, то результаты измерений называют˝равноточными.

Проведение геодезических измерений показывает, что случ˝айные погрешности результатов равноточных измерений обла˝дают

следующими статистическими свойствами, проявляющимися ˝в

больших рядах измерений:

по абсолютной величине погрешности не превышают некоторого предела;

положительные и отрицательные погрешности, равные по абсолютной величине, встречаются в ряду примерно одинако˝во часто;

чем больше погрешность по абсолютной величине, тем она

реже встречается в ряду;

чем больше ряд измерений, тем меньше по абсолютной вели-

1Однородными называют величины одного и того же наименования, а также одного и того же размера или разных размеров (например, угл˝ы), если размер не влияет на величину получаемой погрешности.

278

чине среднее арифметическое значение из погрешностей и п˝ри

достаточно большом числе ï измерений

Случайные погрешности 1, 2, ..., ï равноточных измерений можно рассматривать как значения одной и той же случайной˝ ве-

личины , которую также будем называть случайной погрешностью.

В соответствии с приведенными выше статистическими свой˝-

ствами случайных погрешностей можно подобрать наиболее˝ подходящую вероятностную модель их распределения — закон ˝распределения случайной величины . Такой наиболее простой и

достаточно точной вероятностной моделью распределения ˝слу-

чайных погрешностей измерений является нормальное распределение.

Плотность нормального распределения случайной погрешности

ãäå σ — среднее квадратическое отклонение случайной погрешн˝ости .

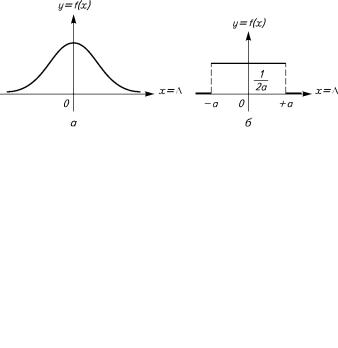
График (рис. 9.1, à) функции (9.21) называют кривой нормального распределения, или кривой Гаусса. Эта кривая симметр˝ична

относительно оси ординат.

Вероятность ð появления погрешности в интервале (õ, õ + dx)

может быть выражена приближенным равенством ð ≈ f(x)dx. На графике (см. рис. 9.1, à) наглядно видны вероятностные свойства

случайной погрешности , имеющей нормальное распределение: положительные и отрицательные значения погрешности, рав˝ные

по абсолютному значению, равновероятны; чем больше погреш˝-

ности, равные по абсолютному значению, тем меньше вероят-

ность их появления.

Рис. 9.1. Графики нормального (à) и равномерного (á) распределения случайной погрешности

279

На основании определения математического ожидания (9.12)

∞

Òàê êàê f(x) — функция четная, то подынтегральная функция xf(x) — нечетная, а потому нетрудно заключить, что значение ин˝- теграла в формуле (9.22) равно нулю, т. е. математическое ожида˝-

ние случайной погрешности равно нулю =

Это свойство случайной погрешности D положено в основу

всей теории случайных погрешностей измерений. Оно соглас˝уется

с четвертым статистическим свойством случайных погрешн˝остей. По закону больших чисел для случайных величин

Нормальное распределение, достаточно хорошо отражая дей˝-

ствительное распределение погрешностей измерений, имее˝т явное отличие от него: действительные погрешности по абсолю˝тно-

му значению не превышают определенного предела, а при нор˝- мальном распределении значение случайной величины може˝т

быть сколь угодно большим. Для практических целей это обс˝тоятельство не имеет существенного значения, так как при нор˝маль-

ном распределении большие по абсолютному значению погре˝ш- ности имеют очень малую вероятность. Учитывая это, обычно˝

считают, что случайные погрешности измерений имеют норма˝ль-

ное распределение или приближенно нормальное.

Говоря о близости распределения погрешностей измерений˝ к нормальному, имеют в виду распределение суммарных погреш˝ностей результатов измерений. Эти погрешности являются сум˝мами элементарных погрешностей, происходящих от отдельных фа˝кторов (причин). Законы распределения элементарных погрешно˝стей могут сильно отличаться от нормального. Так, погрешность ˝отсче-

та по шкале измерительного прибора имеет равномерное рас˝пре-

деление.

Плотность равномерного распределения выражается равен-˝ ствами:

ãäå à — наибольшее значение погрешности (рис. 9.1, á).

280