Маслов А.В., Гордеев А.В., Батраков Ю.Г. - Геодезия

Получив значение ò по этой формуле, находят среднюю квад-

ратическую погрешность среднего арифметического по фор˝муле (9.51):

=

Если подставить выражение для ò из формулы (9.57) в формулу

(9.51), то найдем выражение средней квадратической погрешности Ì через поправки:

Контроль вычисления [υ2] выполняют следующим образом.

Умножив равенство υi = L – li íà υi (i = 1, 2, …, ï) и просуммировав по переменному индексу i îò 1 äî ï, получают [υ2] = –[υl] + L[υ].

По свойству поправок [υ] = 0, поэтому [υ2] = – [υl]. После замены в этом равенстве li íà l0 + εi найдем, что

[υ2] = –[υε].

Существуют и иные формулы для этого контроля, например,

[υ2] = [ε2] – [υ2]/n.

Åñëè L получено с округлением, то указанный контроль не бу-

дет выполняться точно. В этом случае для строгого контрол˝я может быть использовано равенство

[υ2] = –[υε] + (L – l0)[υ].

Приближенный контроль может быть осуществлен с помощью неравенства |[υ2] + [υε]| ≤ 0,5|[ε]| единицы последнего знака L.

П р и м е р. Обработать ряд равноточных измерений угла (табл. 9.3), т. е. н˝айти среднее арифметическое, среднюю квадратическую погрешн˝ость одного измерения и среднюю квадратическую погрешность среднего арифм˝етического.

9.3. Оценка точности измерений по поправкам

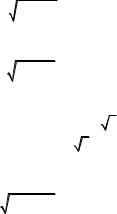
Ê î í ò ð î ë ü: [u] = nw = 5(–0,2²) = –1²; [u2] = –[ue] + (L – l0)[u] = 546 + 13(–1,0) = = 533, = = ¢¢ = = ¢¢ » ¢¢

291

9.12. СРЕДНЯЯ КВАДРАТИЧЕСКАЯ ПОГРЕШНОСТЬ ОДНОГО ИЗМЕРЕНИЯ, ОПРЕДЕЛЯЕМАЯ ПО РАЗНОСТЯМ ДВОЙНЫХ РАВНОТОЧНЫХ ИЗМЕРЕНИЙ

Если каждая из величин данного ряда измерена дважды и все˝ измерения равноточны (например, измерения превышений по

черным и красным сторонам реек при геометрическом нивели˝ровании), то среднюю квадратическую погрешность одного изм˝ере-

ния можно определить по разностям, полученным для каждой пары этих измерений, следующим образом.

Пусть имеется ряд двойных равноточных измерений

′=

Найдем разности

=′ (i = 1, 2, …, ï).

Величины di представляют измеренные значения разностей. При точных измерениях эти разности были бы равны нулю, т. е˝.

истинное значение каждой из них равно нулю. Поэтому на основании формулы (1.25)

Среднюю квадратическую погрешность одной разности вычи˝с- лим по формуле (9.29)

Подставив в это равенство вместо md его выражение (9.60), по-

лучим

Формула (9.61) дает возможность вычислить среднюю квадратическую погрешность одного измерения по разностям двой˝ных

292

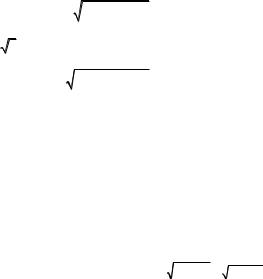
измерений, если в разностях d нет систематических погрешно-

стей. В том случае, когда в них имеется систематическая пог˝решность θ, ее следует определить и из разностей исключить.

Если бы в разностях не было случайных погрешностей, а была˝ только одна систематическая, то все разности были бы равн˝ыθ.

Поэтому можно рассматривать полученные разности как рез˝ультаты равноточных измерений одной и той же величины θ. Тогда

приближенное ее значение получают по формуле среднего ар˝ифметического

Исключив значение θ из разностей di, получим остаточные раз-

ности

Величина –∂i = θ – di представляет собой разность между сред-

ним арифметическим значением θ и результатом измерения di, т. е. имеет тот же смысл, что и поправка υi. На этом основании в

формуле (9.57) вместо υi подставим –∂i, тогда получим

Òàê êàê θ вычисляют как среднее арифметическое, а – ∂i полу- чают как поправку, то для них сохраняются те же контрольны˝е

равенства, которые были указаны в разделе 9.14. Приведем неко˝-

торые из них: [∂] = 0; [∂2] = [∂d]; [∂2] = [d2] – [d]2/ï.

З а д а ч а. Найти среднюю квадратическую погрешность одного измере˝ния угла по разностям двойных равноточных измерений (табл. 9.4)˝.

9.4. Оценка точности по разностям двойных измерений

293

9.13.НЕРАВНОТОЧНЫЕ ИЗМЕРЕНИЯ. ВЕСА ИЗМЕРЕНИЙ

ÈИХ СВОЙСТВА

Если результаты измерений получены в неодинаковых услов˝и- ях и им соответствуют различные дисперсии, а следовательн˝о, и

средние квадратические погрешности, то измерения называ˝ютнеравноточными.

При обработке неравноточных измерений вводят новую хара˝к-

теристику точности измерения — âåñ.

Вес результата измерения ð определяют по формуле

ãäå k — произвольно выбранное число, но одно и то же для всех ве˝сов, участвующих в решении задачи; σ2 — дисперсия результата измерения.

Точное значение дисперсии σ2 никогда не известно, поэтому вес вычисляют по формуле

т. е. принимают σ2 = ò2 (ãäå ò — средняя квадратическая погреш-

ность, полученная по достаточно большому числу результат˝ов измерений).

Òàê êàê k — произвольное число, то вес — относительная характеристика точности, т. е. он дает представление о точно˝сти ре-

зультат измерения только при сравнении с весами других ре˝зуль-

татов.

Как видно из определения веса, отношение весов не изменяе˝т-

ся, если все веса увеличить или уменьшить в одно и то же чис˝ло раз. Это является одним из свойств весов.

Если двум результатам измерения соответствуют веса

т. е. веса двух измерений обратно пропорциональны квадрат˝ам

средних квадратических погрешностей этих измерений.

Равенство (9.68) выражает второе свойство весов.

Из определения веса следует, что равноточные измерения им˝е-

ют равные веса, а неравноточные — неравные. Найдем вес среднего арифметического.

Пусть произведено ï равноточных измерений с дисперсией σ2 = ò2. Веса одного измерения и среднего арифметического соответственно будут ð = k/m2 è Ð = k/M2.

294

Таким образом, в случае равноточных измерений, если вес од˝- ного измерения принят за единицу, то вес среднего арифмет˝иче-

ского равен числу измерений.

З а д а ч а 1. Определить вес дирекционного угла ï-й стороны теодолитного хода, считая исходный дирекционный угол точным, а все изме˝рения правых углов равноточными.

Дирекционный угол ï-й стороны хода определяют из равенства

α = α0 + 180°ï – β1 – β2 – … – βï.

На основании формулы (9.44) напишем выражение для средней ква˝дратиче-

ãäå ò — средняя квадратическая погрешность измеренного угла˝.

Вес дирекционного угла

З а д а ч а 2. Определить зависимость между весом линии, измеренной лен˝- той, и ее длиной s.

Среднюю квадратическую погрешность измерения линии лен˝той определяют

З а д а ч а 3. Найти зависимость между весом линии, определенной по нитя˝- ному дальномеру, и ее длиной s.

При определении длины линии нитяным дальномером отношен˝иеms/s = q — величина постоянная; отсюда ms = qs. Подставив это выражение для ms в формулу

На основании результатов решения задач 2 и 3 можно сказать, ˝что вес линии, измеренной лентой, обратно пропорционален длине лини˝и, а вес линии,

295

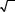
измеренной нитяным дальномером, обратно пропорционален˝ квадрату длины линии.

З а д а ч а 4. Найти вес превышения, полученного в результате геометрич˝е- ского нивелирования хода длиной L.

т. е. вес превышения по всему ходу геометрического нивели˝рования обратно пропорционален длине хода.

9.14. ВЕСА ФУНКЦИЙ ИЗМЕРЕННЫХ ВЕЛИЧИН

Если известны веса аргументов функции, то можно найти и ве˝с

самой функции.

Для различных видов функций можно вывести формулы, по

которым определяют веса этих функций.

Ïðè k = 1 согласно формуле (9.67) ð = 1/ò2, поэтому

Величину 1/ð называют обратным весом.

Рассмотрим различные виды функций и получим для них формулы весов.

1. Функция общего вида

è = f(x1, x2, …, xn).

Для ее эмпирической дисперсии известна формула (9.39).

Заменив в ней дисперсии соответствующими обратными веса˝- ми, согласно формуле (9.76) получим

Так как для этой функции ∂f/∂xi = ki (i = 1, 2, …, ï), то из формулы (9.77) следует

è = kx + c.

296

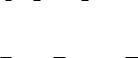
Согласно формуле (9.78)

Здесь ki = ±1 (i = 1, 2, …, ï), поэтому

В случае равноточных измерений, т. е. при ð1 = ð2 = … = ðï = ð, 1/ðè = ï/ð, откуда

Çа д а ч а 1. Найти вес произведения 2β, åñëè âåñ óãëà β равен единице. Согласно формуле (9.79) 1/ð2β = 4/ð2β = 4, откуда ð2β = 1/4 = 0,25.

Çа д а ч а 2. Найти вес среднего арифметического, считая вес одного изм˝ерения равным единице.

Запишем формулу среднего арифметического в виде

= + + +

На основании формулы (9.78) обратного веса линейной функции

= + + +

Òàê êàê ð1 = ð2 = … = ðï = 1, то получим равенство (9.70) Ð = ï.

З а д а ч а 3. Найти вес дирекционного угла ï-й стороны теодолитного хода, вычисленного по формуле α = α0 + 180°ï – [β], считая дирекционный угол α0 точ- ным, а вес каждого измеренного угла равным k.

На основании формулы (9.81) получим выражение (9.72):

ðα = k/n.

9.15. СРЕДНЯЯ КВАДРАТИЧЕСКАЯ ПОГРЕШНОСТЬ ЕДИНИЦЫ ВЕСА

При оценке точности неравноточных измерений в качестве единицы меры дисперсий принимают дисперсию σ измерения,

вес которого равен единице. Так как значение среднего ква˝драти- ческого отклонения σ0 неизвестно, то его заменяют средней квадратической погрешностью μ, соответствующей измерению с весом, равным единице, имея при этом в виду, что μ получена по

297

большому числу измерений и ради краткости ее называют средней квадратической погрешностью единицы веса.

Если дисперсия измерения с весом ð равна σ2 = m2, а с весом единица — σ = μ то по свойству весов [см. формулу (9.68)]:

Найдем выражение средней квадратической погрешности ед˝и- ницы веса μ через погрешности 1, 2, …, ï измерений l1, l2, …, ln,

которым соответствуют веса ð1, ð2, …, ðï.

Нетрудно установить, что величины 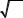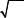ðàâ-

ноточны, их веса равны единице и они имеют погрешности

На основании этого по определению (9.29) можно написать

В целях контроля правильности вычисления μ иногда приме-

9.16. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ ОДНОЙ И ТОЙ ЖЕ ВЕЛИЧИНЫ. СРЕДНЕЕ ВЕСОВОЕ

Допустим, что имеется ï групп равноточных измерений, при этом число измерений в каждой группе соответственно равн˝оð1,

ð2, …, ðï.

По каждой группе получены суммы результатов измерений

298

Среднее арифметическое значение из всех результатов изм˝ере-

ний будет

Lâ = (Σ1 + Σ2 + … + Σn)/(p1 + p2 + … + pn).

Подставив в это равенство вместо Σ1, Σ2, …, Σï их выражения

из формулы (9.88), получим

В этой формуле ði (i = 1, 2, …, ï) — число измерений в i-й группе и в то же время согласно формуле (9.70) — вес среднего ариф˝-

метического li.

Величину Lâ называют средним весовым èëè весовым средним значением.

По формуле (9.89) определяют среднее весовое и в том случае,

когда l1, l2, …, ln получены не как средние значения по группам, а из непосредственных измерений с весами ð1, ð2, …, ðï.

Сокращенно формула среднего весового может быть записан˝а в виде

Для упрощения вычислений используют приближенное значе˝- ние l0, которое выбирают с таким же расчетом, как и при вычисле-

нии среднего арифметического.

Формула среднего весового с приближенным значением имее˝т вид

ãäå ε = li – l0.

Эту формулу выводят так же, как и для среднего арифметиче- ского (9.48). Среднее весовое обладает свойствами, подобными свойствам среднего арифметического.

9.17. ВЕС И СРЕДНЯЯ КВАДРАТИЧЕСКАЯ ПОГРЕШНОСТЬ СРЕДНЕГО ВЕСОВОГО

Запишем формулу (9.89) среднего весового в виде

Lâ = l1p1/[p] + l2p2/[p] + … + lnpn/[p].

Рассматривая Lâ как линейную функцию l1, l2, …, ln и применив

299

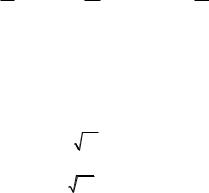
к ней формулу обратного веса (9.78), получим

= + + +

т. е. вес среднего весового равен сумме весов измерений, по˝ кото-

рым оно получено.

Подставив вместо Ðâ его выражение (9.92), получим

ãäå Ìâ — средняя квадратическая погрешность среднего весовог˝о.

9.18.ПОПРАВКИ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ ОДНОЙ

ÈТОЙ ЖЕ ВЕЛИЧИНЫ И ИХ СВОЙСТВА

Если имеется ряд измерений l1, l2, …, ln одной и той же величи-

ны, веса которых соответственно равны ð1, ð2, …, ðn, то поправкой будет разность

между средним весовым и результатом измерения.

Умножив равенства (9.94) на соответствующие веса и просум-

мировав все полученные равенства, найдем

[pυ] = [p]Lâ – [pl].

Подставив в это соотношение выражение среднего весового˝

[pυ] = [p][pl]/[p] – [pl] = 0,

получим

Это равенство выражает одно из свойств поправок, соответ-˝

ствующих случаю неравноточных измерений одной и той же ве˝ли- чины. Свойство поправок (9.95) используют для контроля правильности вычислений Lâ è υi.

Åñëè Lâ получено с округлением, то вместо условия (9.95) должно выполняться равенство [pυ] = [p]ω, в котором ω — погрешность округления.

300