§7. Пучок и связка плоскостей

Пучком плоскостей называется множество всех плоскостей, проходящих через некоторую прямую, называемую осью пучка.

71

Пусть в афинной системе координат ОХУZзаданы две пересе-кающиеся плоскости α₁и α₂своими уравнения вида (3.9) и (3.10) соответственно.

ТЕОРЕМА 3.3. Уравнение вида

α(А₁х+B₁у+C₁z+D₁)+β(А₂х+В₂у+C₂z+D₂)=0. (3.11)

где α и β - некоторые действительные числа одновременно не равные нулю, задает некоторую плоскость пучка, определяемую плоскостями α₁и α₂. Обратно, любая плоскость пучка задается уравнением вида (3.11) при некоторых действительных числах α и β одновременно не равных нулю.

Доказательство проводится аналогично, как и для случая пучка прямых.

Если, например, α0, то, деля обе части (2.11) на α и обозначая β/α=λ, получаем следующее уравнение пучка плоскостей;

А₁х+B₁y+C₁z+D₁+λ(A₂x+B₂y+C₂z+D₂)=0. (3.12)

Связкой плоскостейназывается множество всех плоскостей, проходящих через некоторую точку, называемую центром связки. Если S₀(x₀,y₀,z₀)-центр связки, то уравнение связки с центром в точке S₀имеет вид

А(х-x₀)+В(у-y₀)+С(z-z₀)=0, (3.13)

где А, В и С - произвольные действительные числа, одновременно не равны нулю.

ПРИМЕР 3.1. Составить уравнение плоскости, проходящей череэ точку Р(1,2,3) и прямую, определяемую плоскостями

2х+Зу-z+1=0, х+у-2z-3=0.

РЕШЕНИЕ. Составляем уравнение пучка

2х+Зу-z+1+λ(x+y-2z-3)=0. (*)

Так как искомая плоскость проходит через точку Р, то, подставляя координаты точки Р в уравнение(*),найдем значение λ=1

72

Итак, искомое уравнение имеет вид

2x+Зу-z+1+х+у-2z-3=0, т.е. Зх+4у-3z-2=0.

§8. Угол между двумя плоскостями

Пусть даны плоскости α₁и α₂своими уравнениями вида (3.9)и (3.10) соответственно. Тогда под углом между плоскостями α₁и α₂понимают наименьший угол, на который надо повернуть одну из плоскостей до ее совпадения с другой плоскостью. Поэтому, если φ - угол между плоскостями α₁и α₂, то. Очевидно, что либо φ=(^,), либо φ= (-^,), где и- нормальные векторы плоскостей α₁и α₂соответственно. В любом случае

(3.14)

В частности, если φ=π/2, то

А₁A₂+В₁B₂+С₁C₂=0 (3.15)

- условие перпендикулярности двух плоскостей.

73

IV прямая в пространстве.

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ

§1. Уравнение прямой в пространстве

Очевидно, что прямую в пространстве можно задать как линию пересечения двух плоскостей α₁и α₂. Тогда в произвольной афинной системе координат прямая задается системой двух линейных уравнений

(4.1)

- общее уравнение прямой или уравнение прямой в общем виде.

Ясно, что любая система вида (4.1), с непропорциональными коэффициентами при неизвестных, определяет в пространстве некоторую прямую.

Пусть l-прямая. Тогда ее положение в пространстве одно

з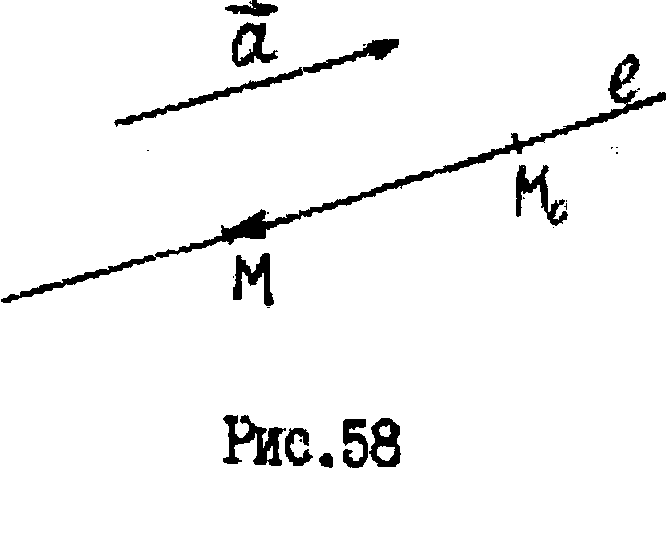начно определяется заданием ее направляющего вектора=(m,n,р) и точкой М₀(х₀,у₀,z₀), через которую прямая проходит (Рис. 58). Возьмем произвольную точку М(х,у,z)l. Тогдаи, значит,

(4.2)

Очевидно, что равенство (4.2) выполняется тогда и только тогда, когда точка Мl, т.е. равенство (4.2) является уравнением прямой в векторной форме. Переходя к координатам, получим

74

x-x₀=tm

y-y₀=tn (4.3)

z-z₀=tp

• параметрические уравнение прямой, проходящей через точку

M₀(x₀,y₀,z₀)параллельно вектору=(m,n,р). Выражая параметр t, в (4.3), получим

(4.4)

- каноническое уравнение прямой, проходящей через точкуМ₀(х₀y₀,z₀) параллельно вектору=(m,m,р).

Уравнение (4.4) можно записать, например, в виде следующей системы

(4.5)

Тем самым прямая lпредставляется как линия пересечения двух плоскостей, параллельных соответственно оси OZ и оси ОУ.

Прямая однозначно определена, если известны две точки чере( которые она проходит. Пусть M₁{x₁,у₁,z₁)lи М₂(х₂,у₂,z₂)l. Тогда в качестве направляющего вектора прямойlможно взять

вектор =(х₂-х₁,у₂-у₁,z₂-z₁). Уравнение (4.4) в этом

случае примет вид

(4.6)

- уравнение прямой, проходящей через две заданные точки.

Решим задачу приведения общего уравнения прямой к каноничес-

75

кому виду. Обозначим ₁=(А₁,В₁,С₁)

₂=(А₂,В₂,С₂) - нормальные векторы соответственно плоскостей α₁и α₂

(Рис. 59). Очевидно, что ₁ ┴lи

₂┴l. Следовательно, вектор =x

коллинеарен прямой lи его можно взять в качестве наиравлявдего вектора прямойl. Из (1.37) следует, что

Беря произвольную точку М₀(х₀,у₀,z₀), удовлетворяющую системе (4.1), окончательно получаем

(4.7)

- каноническое уравнение прямой.

ПРИМЕР 4.1. Привести к каноническому виду уравнение прямой

РЕШЕНИЕ. Найдем направляющий вектор а прямой.

Найдем точку, принадлежащую прямой. Пусть, например, z=0, тогда легко видеть, что х=-1, у=-1. Следовательно,

- искомое уравнение прямой.

76