§8. Угол между двумя прямыми

Под углом φ между двумя прямыми l₁ иl₂будем понимать наименьший угол, на который надо повернуть одну прямую, чтобы она стала параллельной другой прямой или совпала с ней.

Пусть прямые заданы общими уравнениями (2.18). Очевидно, что

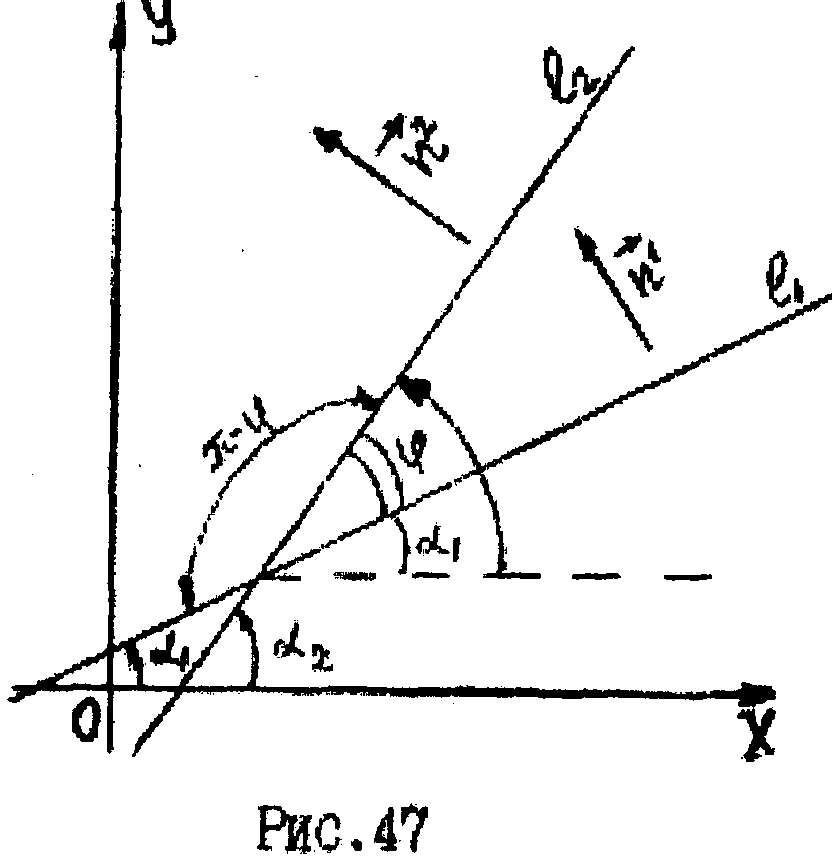соsφ=|cos|(рис. 4?). Тогд Тогда

cosφ==

(2.31)

Заметим, что выражение для cosφ взято по абсолютной величине, так как

и cosφ0,

Пусть теперь прямые l₁иl₂задана уравнениями с угловыми коэффициентами k₁вk₂соответственно. Тогда легко видеть, что φ=α₂-α₁Следовательно,

В силу того, что ипоследнее выражение берем также по модулю. Итак,

(2.32)

Наконец, если прямые заданы каноническими уравнениями <2.16), то либо , либо.Тогда

(2.33)

61

ПРИМЕР 2.8. Составить уравнение прямой, проходящей через точку M₁(2,l) под углом 45° к прямойl: 2х+Зу+4=0.

РЕШЕНИЕ. Из Рис.48 следует, что существуют две прямые l₁иl₂Удовлет воряющие условию задачи. Найдем угловые коэффиилентыk₁и k₂искомых прямых. Так как для прямойlее угловой коэффициент k=-2/3, то

Если , то 3-2k=-2-3k и

К₁=-5. Если, то З-2к=2+3к и к₂=1/5

-Следовательно, прямыe l₁ и l₂, задаются уравнениями:

у-1=-5(х-2); у-1=1/5(х-2)

Итак, l₁:у+5х-11=0;l₂:5у-x-3=0 - искомые уравнения

§9. Расстояние от точки до прямой

Пусть требуется найти расстояние d от точки М₀(x₀,у₀)

д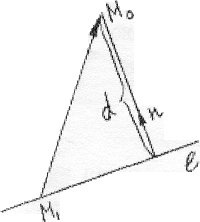о прямой l, заданной уравнением Ax + +By+С=0. Возьмем на прямой точку

M₁(х₁,у₁) и обозначим=(x₀-x₁,

Y₀-y₁) (рис.49)- Тогда

=

Рис.49

=

62

Так как координаты точки М₁удовлетворим уравнению прямойl, то -Ax₁-By₁-С. Тогда окончательно получаем

(2.34)

63

III плоскость

§1. Общее уравнение плоскости

Пусть в прямоугольной системе координат OXYZ задана плос

кость α, проходящая через точку М₀(х₀,

у₀,z₀). Возьмем произвольную точку М(х,у,z)α и обозначим(А,В,C) -нормальный вектор плоскости α(Рис.50)

Очевидно, что , т.е.

Рис.50

А(х-х₀)+В(у-у₀)+C(z-z₀)=0 (3.1)

Так как точка М взята произвольно, то уравнению (ЗЛ) удовлетворяет любая точка плоскости α. Пусть теперь точка M₁(х₁,у_1,z₁) удовлетворяет уравнению (3.1). Тогда

А(х₁-x₀)+B(y₁-y₀)+C(z₁-z₀)=0

и, значит, точка М₁принадлежит плоскости α. Уравнение (3.1) называетсяуравнением плоскости, проходящей через заданною точку.

Раскроем скобки в (3.1) и обозначим D=-Аx₀-Ву₀-Cz₀.Получим

Ax+By+Сz+D=0 (3.2)

-уравнение плоскости в общем видеилиобщее уравнение плоскости. Уравнение вида (3.2) называется линейным относительно переменныхx, у и z, если А²+В²+С²0.

ТЕОРЕМА 3.1. Любая плоскость в произвольной афинной системе Ординат O'X'Y'Z' задается линейным уравнением вида (3.2). Обратно, всякое линейное уравнение вида (3.2) является уравнением

64

плоскости.

Доказательство. Пусть ОXYZ- прямоугольная система координат. Тогда, как было показано выше, уравнение (3.2) является уравнением плоскости в этой системе координат. Перейдем к новой афинной системе координат O'X'Y'Z', Для этого воспользуемся формулами преобразований (1.50)

x=α₁₁x'+α₁₂y'+α₁₃z'+α₁,

y=α₂₁x'+α₂₂y'+α₂₃z'+α₂,

z=α₃₁x'+α₃₂y'+α₃₃z'+α₃.

Подставляя в (3.2) м приведя подобные, получаем

А₁x'+В₁y'+C₁z'+D₁=О (*)

Покажем, что А₁²+B₁²+С₁²0. Предположим противное,т.е. А₁=

=B₁=C₁=0. Если D0, то уравнение (А) не удовлетворяет ни одна из точек плоскости, значит, и уравнение (3.2) не задает ни одну из точек плоскости. Если D=0, то уравнению (*) удовлетворяют все точки пространства, значит, и уравнению (3.2) удовлетворяют все точки пространства. Противоречие. Это означает, что уравнение плоскости в произвольной афинной системе координат задается линейным уравнением вида (3.2).

Докажем обратное утверждение. Пусть дано линейное уравнение вида (3.2) и пусть точка M₀(x₀,y₀,z₀)удовлетворяет этому уравнению. Тогда

Ax₀+By₀+Cz₀+D=0 (**)

Вычтем из (3.2) равенство (**). Получим

А(х-х₀)+В(у-у₀)+С(z-z₀)=О

Последнее уравнение эквивалентно уравнению (3.2) и, как показано выше, задает плоскость. Теорема доказана.

65

Рассмотрим некоторые частные Случаи уравнения (3.2)*

1) Пусть D=0, тогда Ax+By+Сz=0 - уравнение плоскости, проходящей через начало координат.

2) А=0, тогда By+Сz+D=0 - уравнение плоскости, параллельной оси ОХ. При этом плоскость не имеет с осью ОХ общих точек, если D0 (FMC. 52), и проходит через эту ось, вели D=0 (Рис.53).

3) А=0, В=0, тогда Сz+D=0 - уравнение плоскости, параллельной плоскостиOXY. При этом плоскость отлична от плоскости OXY, если D0 (Рис. 52), к совпадает с ней, если D=0. Таким образом уравнение плоскости ОП можно записать так ОХУ

Z=0.

Аналогично рассматриваются и другие случаи равенства нулю некоторых коэффициентов уравнения (3.2).

Пусть в уравнении (3.2) все коэффициенты отличны от нуля. Тогда Ах+By+Сz=-D, т.е.

Обозначим -D/A=a, -D/B=b, -D/C=c. Тогда

(3.3)

- уравнение плоскости в отрезках. Числа |а|, |Ь|, |с| указывают на величины отрезков, отсекаемых плоскостью на координатных осях.

66

§2.Геометрический смысл знака выражения Ах₁+Ву₁+Cz₁+D

Выясним геометрический смысл выражения Аx₁+Ву₁+Cz₁+D,

где М₁(x₁,у₁,z₁) - произвольная точка пространства, Ax+By+Cz+D=0-уравнение плоскости α. Обозначим через М₀ортогональную проекцию точки М₁на

плоскость α(Рис, 54).Тогда ||

и, в силу теоремы 1.1.

=t (3.4)

Рис.54

Запишем равенство (3.4) в координатной

форме. Тогда

x₁-x₀=tA, y₁-y₀=tB, z₁-z₀=tCт.е.

х₁=x₀+tA,y₁=y₀+tВ,z₁=z₀+tC.

Следовательно,

Аx₁+ By₁+Cz₁+D=А(x₀+tA)+В(у₀+tB)+С(z₀+tC)+D =

=Аx₀+By₀+Cz₀+D+t(A²+В²+C²).

Так как Ах₁+By₁+Cz₁+D= 0, то окончательно получим

Ах₁+By₁+Cz₁+D=t(A²+В²+С²). (3.5)

Если Аx₁+By₁+Cz₁+D>0, то и t>0, т.е. вектору и, в силу равенства (3.4). одинаково направлены. Значит,

векторы инаходятся по одну сторону от данной плоскости. И обратно, если точка М₁и векторрасположены по одну сторону от данной плоскости, то векторыиодинаково направлены. Следовательно, в силу равенства (3.4), t>0

67

Ax₁+By₁+Cz₁+D>0.

Аналогичным образом доказывается, что Ах₁+Ву₁+Cz₁+D<0

тогда и только тогда, когда векторы ирасположены по разные стороны от данной плоскости.