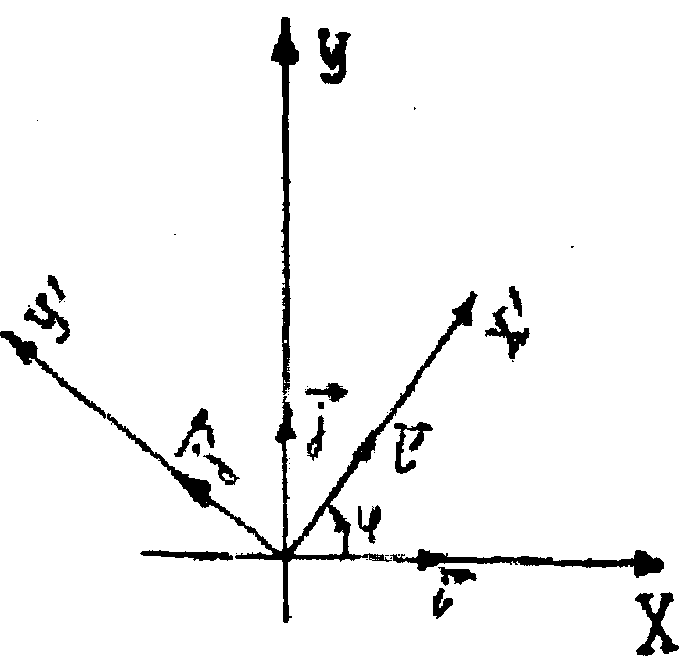
§20. Прямоугольные координаты на плоскости

Пусть дана старая м новая прямоугольные системы координат,

соответственно (0,,) и (О',',') (Рис. 32). Обозначив через (φ угол между векторами и'Тогда

'=cosφ+sinφ,

'=(-cos(π/2-φ))+sin(π/2-φ)=

=-sinφ+cosφ.

Если точка О'имеет координаты (α,β) относительно стари системы координат, то из формул (1.46) следует:

Рис.32

x=x'cosφ-y'sinφ+α,

(1.52)

y=x'sinφ+y'cosφ+β

В частности, если =' и='(Рис.33) ,то формулы

Рис.33 Рис.34

(1.52) принимают вид

х=х'+α,у=у'+β (1.53)

- формулу преобразования координат при параллельном переносе системы координат

42

Если же точки 0 и 0' совпадают (Рис.34), то формулы (1.52) принимают вид

x=x'cosφ-y'sinφ,

(1.54)

y=x'sinφ+y'cosφ.

- формулы преобразования координат при повороте системы координат вокруг начала на угол φ

43

Iiпрямая на проскости

Прежде чем перейти к изучению прямой на плоскости, остановим-ся на некоторых самых общих понятиях и определениях, необходимых дальнейшем.

Фигурой (линией, поверхностью и т.д.) назовем произвольное

множество точек пространства. Зафиксируем некоторую афинную систему координат OXYZ. Тогда уравнение

f(х,у,z)=0 (*)

называется уравнением фигуры Ф, если ему удовлетворяют координаты (α,β,γ) любой точки этой фигуры, и любая упорядоченная тройка чисел (α,β,γ), удовлетворяющая уравнению (*). представляет собой координаты некоторой точки фигуры Ф. Очевидно, что фигура определяется своим уравнением. Составление уравнения фигуры состоит в алгебраической записи свойства, характеризующего все точки этой Фигуры и только их. Эта запись должна связывать текущие координаты произвольной точки фигуры с теми постоянными величинами, которые определяют фигуру. Если точка M(x,у,z) принадлежит фигуре Ф (не принадлежит Ф), то будем писатьM(х,у,z)Ф (М(х,у,z)Ф). Тогда следующее уравнение

f(x,y,z)=(2.1)

задает произвольную фигуру Ф. Из построения следует, что одна и та же фигура Ф может задаваться бесконечным множеством различных уравнений. Для этого достаточно в уравнении (2.1) единицу заменить на любое отличное от нуля число.

ПРИМЕР 2.1. Составить уравнение геометрического места

центров окружностей, касающихся оси ОХ и проходящих через точку А(3, 4).

44

PEШEHИЕ. Возьмем произвольную точку М(х.у), принадлежащую данной фигуре (Рис. 35). Тогда имеет место следующее равенство:

(х-З)²+(у-4)²=у², т.е.

х²-6х-8у+25=0.

Последнему уравнению удовлетворяют координаты всех точек фигуры и только они, значит, полученное уравнение является искомым.

Рис. 35

ПРИМЕР 2.2. Определить вид линии, задаваемой уравнением

Х²+у²+2х-10у+1=0.

РЕШЕНИЕ. Выделим полные квадраты при неизвестных х и у.

Получим

Х²+2х+1+у²-10у+25-25=0. т.е.

(х+1)²-(у-5)²=25 - уравнение окружности с центром в точке 0(1,5) и радиусомr= 5.

ПРИМЕР 2.3. Найти уравнение циклоиды, которая определяется как путь, описываемый одной из точек М окружности, катящейся без скольжения по неподвижной прямой.

РЕШЕНИЕ. Выберем прямоугольную систему координат таким образом, чтобы в начальный момент времени точка М совпадала с началом координат (Рис, 36). Тогда, через некоторый момент времени катящаяся окружность повернется на угол t и точка А станет ее новой точкой касания. Так как качение происходит без скольжения, то ддина дуги МА равна длине отрезка ОА, следовательно. ОА=Rt, где R -Рис. 36 радиус окружности. Обозначим координата точки М через х и у. Тогда

Рис.36

45

х=Пр_ОХ=пр_ОХ+пр_ОХ+пр_ОХ

(2.2)

У=Пр_ОУ=пр_ОУ+пр_ОУ+пр_ОУ

Следовательно,

пр_ОХ=Rt, пр_ОХ=0, пр_ОХ=-Rsint

(2.2)

пр_ОУ=0, пр_ОУ=R, пр_ОУ=-Rcost

Подставляя эти значения в (2.2), окончательно получаем

х=R(t-sint), у=R(1-cost) (2.3)

- параметрическое уравнение циклоиды.

ПРИМЕР 2.4. Найти параметрическое уравнение окружности радиуса r>0 с центром в начале координат.

РЕШЕНИЕ. Возьмем произвольную точку М(х,у) окружности и обозначим через t угол между радиус-вектороми осью ОХ в положительном направлении (Рис.37). Тогда

х=rcost, у=rsint (2.4)

- параметрическое уравнение окружности с центром в начале координат и радиусом, рав-

ным r. Очевидно, что 0<t<2π Из уравнений (2.4) следует, что

Рис. 37

X²=r²cos²t,у²=r²sin²t, т.е. х²+y²=r².

46