§1. Прямая на плоскости

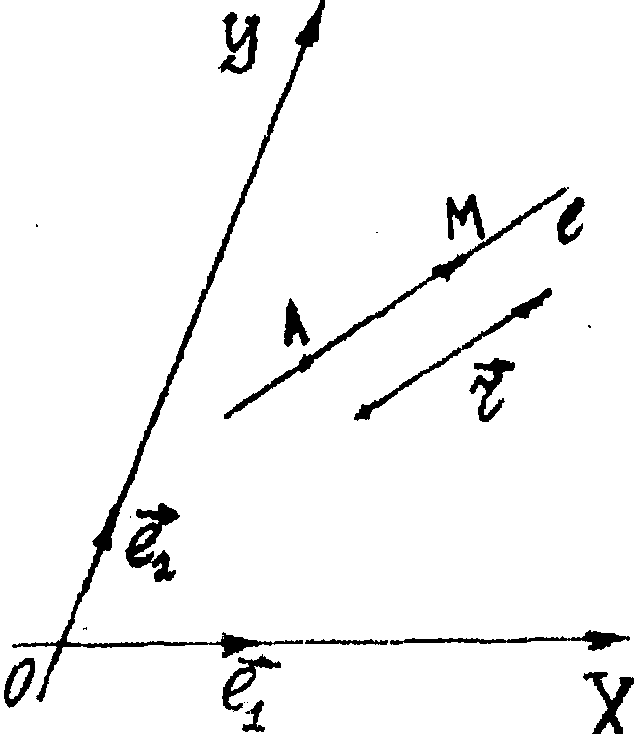
Пусть в плоскости α задана афинная система координат (0,

,) и прямаяl, принадлежащая этой плоскости α (Рис. 38). Составим уравнение прямойl. Заметим, что положение прямойlоднозначно определено, если известен вектор, коллинеарный этой прямой и называемый направляющим вектором прямой, и точка, через которую прямая проходит. Очевидно, что в качестве направляющего вектора прямой можно взять Рис.38 любой вектор, коллинеарный данной прямой. Пусть= (m₁,n₁) и=(m₂,n₂)-

Рис.38

- какие-либо направляющие векторы прямой l. Тогда из необходимого и достаточного условия коллинеарности двух векторов следует, чтоm₁/m₁=n₂/n₂не параллельна оси OY, то

следовательно,

(2.5)

- угловой коэффициент относительно выбранной системы координат.

В частности, для прямоугольной системы координат (0,)

к=tgα, где α- угол между осью ОХ и любым направляющим век

Рис.39. Рис.40.

47

тором прямой l(Рис. 39). Угол α называетсяуглом наклона прямой l к оси ОХ.

Если прямая lпараллельна оси ОУ, тоlпересекает осьOХ в некоторой точке Р(а,0) (Рис. 40). Тогда все точки прямой и только они удовлетворяют соотношению

x=a (2.6)

- уравнение прямой, проходящей через точку Р(а,0) параллельно оси ОУ. Заметим, что в качестве направляющего вектора такой прямой можно взять вектор(0,р), где р - произвольное отличное от нуля число. В этом случае, как видкм. угловой коэффициент прямой не существует.

Пусть прямая lпроходит через точкуA(а,b) и имеет угловой коэффициент k (Рис. 38). Возьмем произвольную точку М(х,

у) на прямой l.Тогда=(х-а, у-b) - направляющий вектор прямойl. Из (2.5) теперь следует, что

(2.7)

Отсюда

у-b=k(x-а) (2.8)

Итак, любая точка прямой lудовлетворяет уравнению (2.8). Покажем, что любая точка М₁(х₁,у₁), удовлетворяющая уравнению (2.8) и отличная от точки А, лежит на прямойl. Так как точка M₁отлична от точки А, то х-а0. Значит,

Это означает, что направляющие векторы прямых lи АМ₁колли- арными,так как эти прямые проходят через общую точку А, то они

48

совпадают. Следовательно, точка M₁лежит на прямойl.

Таким образом, уравнение (2.8) задает прямую, имеющую угловой коэффициент k и проходящую через точку А (а,b).

Если, в частности, точка А лежит на оси OY, т.е. а=0,то уравнение (2.8) принимает вид

у=kx+b. (2.9)

Если прямая параллельна оси ОХ и проходит через точку Р(0, b),то к=0 и ее уравнение принимает вид

у=b. (2.10)

§2. Общее уравнение прямой. Уравнение прямой в отрезках

Пусть задана некоторая афинная система координат OXY.

ТЕОРЕМА 2.1. Любая прямая lсистеме координат ОXзадается линейным уравнением вида

Аx+By+С=О, (2.11)

где А,В,С R и А²+В²0. Обратно, любое уравнение вида (2.11) задает прямую.

Доказательство. Пусть прямая lпараллельна оси OY. Тогда, ее уравнение, согласно (2.6), имеет вид

х-а=0.

Если же прямая lне параллельна оси OY,то из (2.8) следует, что у-b=kx-ka. т.е. у-kx+С=0 - уравнение вида (2.11)

где C=ka-b. , Докажем теперь обратное утверждение. Пусть задано уравнение

вида (2.11). Если В_i0, то By=-Ax-С, у=-Ax/B-C/D т.е. у=kx+b, гдеk=-Ax/B, b=-C/B. Но последнее уравнение задает прямую с угловым коэффициентом k, проходящею через точку Р(0,b).

49

Если же В=0, то Ах+С=0, и так как А0. то х=-С/А- уравнение прямой, параллельной оси OY. Теорема доказана.

Уравнение вида (2.11) называется общим уважением прямой. рассмотрим некоторые частные случаи этого уравнения.

1. С=0. Тогда Ах+By=0 и, значит, прямая lпроходит через начало координат. Обратно, если прямаяlпроходит через начало координат, то А0+В0+C=0, т.е. С=0. Итак,прямаяlпроходит через начало координат тогда и только тогда, когда свободный член С ее уравнения (2.11) равен нулю.

2. В=0. С0. Тогда Ах+С=0, т.е. х=-C/Aи прямаяlпараллельна оси OY, и не совпадает с ней (С0).

3. В=0, С=0, т.е. х=0 - уравнение оси ОУ.

4. А=0. С0. Тогда By+C=0. т.е. у=-C/Bи прямаяlпараллельна оси ОХ и не совпадает с ней (С0).

5. А=0,С=0, т.е. у=0 - уравнение оси ОХ.

Пусть в уравнении (2.11) все коэффициенты А, В и С отличны от нуля. Тогда

-Ах-By=-С, и.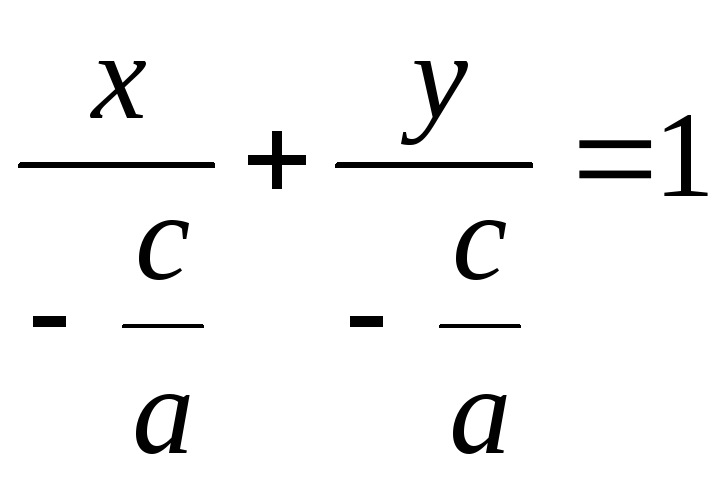

Обозначим -С/А=а, -С/B=b. Получим

(2.12)

- уравнениев отрезках. Действительно, числа |а| и|b| указывают на величины отрезков, отсекаемых прямойlна осях ОХ и OY соответственно (Рис. 40).

Рис.40

Пусть прямая lзадана общим уравнением (2.11) в прямоугольной системе координат и пусть точкиM₁(x₁,у₁) и М₂(х₂,у₂) принадлежитl. Тогда

50

Аx₁+Ву₁+С=Ах₂+Ву₂+С. т.е.A(x₁-x₂)+В(у₁-у₂)=0.

Последнее равенство означает, что вектор =(А,В) ортогонален вектору=(x₁-x₂,у₁-у₂). т.е.Вектор(А,В) называетсянормальным вектором прямой l.

Рассмотрим вектор =(-В,А). Тогда

=А(-В)+ВА=0. т.е. ┴.

Следовательно, вектор =(-В,А) является направляющим вектором прянойl.