МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ

БЕЛАРУСЬ

ГОМЕЛЬСКИЙ ГОСУДАРСТВЕЕНЫЙ УНИВЕРСИТЕТ

ИМЕНИ Ф.СКОРИНЫ

Кафедра алгебры и геометрии

А.Д.Ходалевич, В.М.Селькин, В.В.Аниськов

Краткий курс лекций по геометрии и алгебре

(специальность - "Прикладная математика")

"Аналитическая геометрия", ч 2.

Гомель 1997

УДК 514 122

Рецензенты: Семенчук В.Н. - кандидат физико-математических наук.

Сидоров А.В. - кандидат физико-математических наук.

Дается краткое изложение курса лекций по аналитической

геометрии для студентов, обучающихся по специальности

"Прикладная математика"

Рекомендовано к печати ученым советом Гомельского

государственного университета им. Ф.Скорины.

©Гомельский государственный университет им. Ф.Скорины

Глава I кривые второго порядка

§ 1. Парабола

Пусть в прямоугольной системе координат ОХУ задана парабола уравнением

y = ах²+ Ьх + с.

Выделяя полный квадрат при переменной х, данное уравнение можно записать в следующем виде

Осуществим параллельный перенос в новую систему координат

О^'Х^'Y^', используя формулы

Тогда у'=а(х')².Таким образом, можно считать,что в прямоуголь-

ной системе координат парабола задается уравнением

у=ах².

Повернем систему координат ОХУ на угол φ где φ= /2, еслиa>0

и φ= 3/2, если а<0. Пусть, например, а>0. Тогда

3

Следовательно, в новой системе координат 0^'Х^'Y^'уравнение пара

болы примет вид

х'=а(у')², т.е.

Обозначим 1/а = 2р, тогда (y')²=2рх', где р >0. Итак, в прямо-

угольной системе координат парабола задается уравнением вида

y' = 2рх, p>0 (1.1)

• каноническое уравнение параболы.

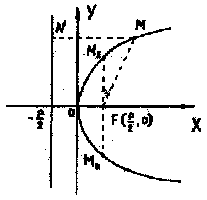
Выясним геометрический

смысл коэффициента р. Для

этого возьмем точку F(p/2,0),

называемую фокусом пара-

болы (1.1) и прямую х=

—(р/2), называемую дирек-

трисой параболы (рис. 1).

Обозначим через М(х,у)

произвольную точку на пара-

боле. Тогда расстояние MN

от точки M до директрисы

равно

Рис.1.

Вычислим расстояние MF от точки M до фокуса F.

Итак, MN = MF, следовательно, все точки параболы равноудалены от ее фокуса и директрисы. Обратно, если точка M такова, что MN =

4

MF, то

,

значит,

т.е. у²= 2ps. Следовательно, точка М лежит на параболе (1.1).

Вывод: Если в прямоугольной системе координат OXY задана

парабола у²= 2рх, то это есть множество всех точек плоскости,

равноудаленных от фокуса F и директрисы d.

Если теперь на плоскости дана произвольная точка F и прямая d, не проходящая через эту точку, то можно провести ось ОХ через точку F перпендикулярно прямой d. Через середину отрезка, заключенного между точкой F и прямой d, проведем ось OY. Обозначим F(p/2,0), тогда прямая d задается уравнением

x=-(р/2). Это означает, что в построенной системе координат OXYканоническое уравнение параболы имеет вид y²= 2рх.

Предыдущие рассуждения позволяют теперь дать определение па

раболы, не связанное с системой координат.

Определение 1.1.Параболой называется геометрическое место

точек плоскости, равноудаленных от некоторой точки,называемой фокусом параболы и некоторой прямой, называемой директрисой параболы.

Следующие свойства параболы непосредственно следуют из

свойств уравнения (1.1).

1.Абсцисса любой точки параболы неотрицательна.

2.Парабола проходит через начало координат.

3.Парабола симметрична относительно оси абсцисс.

4.При неограниченном возрастании абсциссы xордината у возрастает по абсолютной величине.

5

Величина р в уравнении (1 1) называется фокальным параметром

или просто параметром параболы. Укажем еще одно геометрическое истолкование параметра р. Для этого проведем прямую х = р/2 и обозначим точки пересечения прямой с параболой через M₁(x₁,y₁) и М₂(х₂,y₂) (рис.1). Так какx₁=x₂=p/2, то у²=p²т.е. у=р. Итак, параметр р параболы равен длине перпендикуляра к оси ОХ, восстановленного из фокуса до точки пересечения с параболой. Таким образом, параметр р характеризует форму и размеры параболы.

Наряду с уравнением (1.1) часто приходится рассматривать уравнения вида у²=—2рх, х²=2ру, х²=—2ру (рис.2,а,б,в).

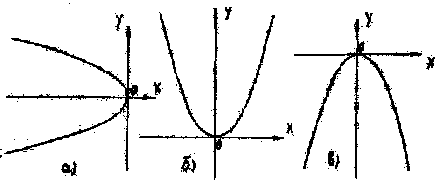
Рис. 2.

Решим задачу о количестве точек пересечения параболы у²=2pxс прямой у = kx+b. Так как у²=k²x²+2kxb+b²,то 2рх=k²х²+2kbх+b².

Следовательно,

K²x²+2(p-kb)x+b²=0 (*)

Теперь, в зависимости от количества корней уравнения (*), возможны три случая:

1) прямая пересекает параболу в двух точках;

2) прямая имеет с параболой одну общую точку;

3) прямая не имеет с параболой общих точек.

6