§3. Уравнение плоскости, проходящей через три заданные точки

Очевидно, что плоскость единственным образом определяется

тремя точками, не лежащими на одной прямой. Пусть это будут точки: А(х₁, у₁,z₁), В(x₂,у₂,z₂),C(x₃,у₃,z₃). Возьмем произвольную точку М(х,у,z) на плоскости α и обозначим вектора

=(x-x₁,y-y₁,z-z₁),

=(х₂-х₁,у₂-у₁,z₂-z₁),

=(x₃-x₁,у₃-y₁,z₃-z₁) (Рис. 55).

Рис.55

В ему необходимого и достаточного условия компланарности трех векторов, получаем

(3.6)

- уравнение плоскости, проходящей через три заданные точки. В частности, если А(а,0,0), В(0,b,0),C(0,0,с), то уравнение (3.6) примет вид

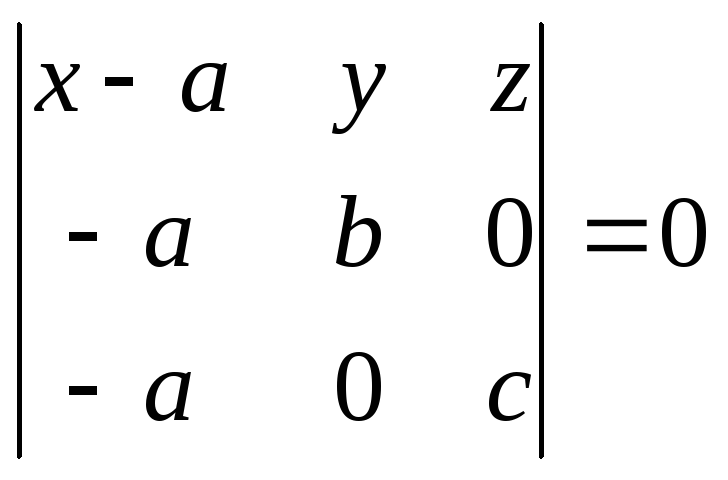, т.е.

68

§4.Нормальное уравнение плоскости

Пусть задана плоскость α и пусть - единичный, вектор

нормали к плоскости α проведенный из начала координат (Рис. 56). Обозначим через М₁(x₁,у₁,z1) ортогональную проекцию точки 0(0,0,0) на плоскость α. Очевидно, что ||=р - расстояние от начала координат до плоскости α.

С другой стороны, для любой точки М(х,у,z)α

Следовательно, из определения скалярного произведения получаем, что

=p (*)

Так как =(х,у,z),=(cosα, cosβ, cosγ),где α, β, γ -

углы, образованные вектором соответственно с осями OX, OY

0Z, то равенство (*) можно записать так;

xcosα+ycosβ+zсозγ-p=0 (**)

- нормальное равнение плоскости.

Отметим, что для преобразования общего уравнения плоскости (3.2) в нормальное надо умножить обе части уравнения (3.2) нормирующий множитель

69

§5. Расстояние от точки до плоскости

Пусть требуется найти расстояние dот точкиM₀(x₀,y₀,z₀)

до плоскости α, заданной уравнением вида (3.2).Обозначим через М₁(x₁,у₁,z₁)ортогональную проекцию точки М₀на плоскость α (Рис. 5?). Тогда и

следовательно"

.(*)

В координатной форме равенство (*) примет вид

А(х₀-x₁)+В(y₀-у₁)+C(z₀-z₁)=

=Ах₀+Ву₀+Сz₀-(Ах₁+By₁+Cz₁)=.

Так как Аx₁+Ву₁+Сz₁=D, то окончательно получаем

(3.8)

§6. Взаимное расположение двух плоскостей

Пусть плоскости α₁и α₂заданы уравнениями вида

α₁: А₁х+B₁y+C₁z+D₁=0, (3.9)

α₂: А₂х+В₂y+С₂z+D₂=0. (3.10)

ТEOPEMA 3.2. Тогда и только тогда плоскости α₁и α₂:

70

1) совпадают, когда А₁=λA₂, B₁=λB₂, C₁=λC₂, D₁=λD₂;

2) параллельны и различны, когда

A₁=λA₂, В₁=λВ₂,С₁=λС₂,D₁λD₂;

3)пересекаются, когда коэффициенты А₁, В₁, С₁не цропор-циональны коэффициентам А₂, В₂, С₂

Доказательство. 1) очевидно, что α₁||α₂тогда и только тогда, когда, т.е. A₁=λA₂, В₁=λВ₂,С₁=λС₂для некоторого λ€R. Если D₁=λD₂, то уравнение (3.9) можно записать в следующем виде;

а₁: λA₂x+λВ₂y+λС₂z+λD₂=0, т.е.

A₂x+В₂y+С₂z+D₂=0

Итак, плоскость α задается точно таким же уравнением, что и плоскость α, значит, эти плоскости совпадают. Обратно, если плоскости α₁и α₂совпадают, то для любой точки М₀(x₀,y₀,z₀)α следует, что М₀€ α. Запишем уравнения плоскостей α₁и α₂в следующем виде;

а₁: λA₁x₀+λВ₁y₀+λС₁z₀+D₁=0

а₂: λA₂x₀+λВ₂y₀+λС₂z₀+D₂=0

Тогда

D₁=-λA₂x₀-λВ₂y₀-λС₂z₀=λD₂

Тем самым случай 1) доказан. Теперь 2) следует из 1). а 3) следует из 1) и 2). Теорема доказана.