Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Киевский национальный университет им. Т. Шевченко

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ovta-zbirnyk-zadach

.pdf

Скачиваний:

Добавлен:

07.03.2016

Размер:

1.46 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 148 9 10 11 12 13 14 > Следующая >>>

9.2.Диференціальні операції

укриволінійних координатах

Основні властивості диференціальних операцій, розглянуті раніше, зберігаються й при використанні криволінійних координат і локального базису. Насамперед, зберігаються всі інваріантні співвідношення (незалежні від вибору базису), зокрема диференціальні векторні тотожності (див. задачі 8.2–8.15).

Суттєва відмінність криволінійного базису від декартового полягає в тому, що криволінійний базис – локальний (залежить від точки простору), і використовувати (8.1)–(8.5), справедливі для декартових координат, не можна. Базисні вектори ei зале-

жать від координат qi і разом із координатами векторів підлягають диференціюванню. Наприклад, для дивергенції векторного поля A = A(1)e(1) + A(2)e(2) + A(3)e(3) , використовуючи векторну

тотожність, можна записати

3	3	3
div ∑ A(i)e(i) = ∑ div( A(i)e(i) ) = ∑(A(i)
i=1	i=1	i=1

div e(i) + e(i) A(i) )

(у декартових координатах перший доданок у дужках відсутній). Нагадаємо, що індекс векторів фізичного базису беремо в дужки, але в прикладних фізичних задачах замість індексу у вигляді цифри у круглих дужках використовують літеру, що позначає відповідну криволінійну координату. Наприклад, eρ, eϕ,

ez – відповідно орти фізичного базису e(1) ,e(2) ,e(3) у циліндрич-

ній системі координат. Аналогічно поступаємо і з індексами

компонент векторів у фізичному базисі. Наприклад, Аρ, Аϕ, Аz – відповідно компоненти вектора А(1), А(2), А(3) у циліндричній системі координат.

Основні диференціальні операції в ортогональних криволінійних координатах мають вигляд:

e(1)

∂f

e(2)

∂f

e(3)

∂f

∂q1

∂q2

∂q3

∂( A H

)

∂(H A H

)

∂(H H

A )

div A =

(1)

(2)

2 (3)

H H

∂q

1 2

∂q

H1e(1)

H2e(2)

H3e(3)

rot A =

∂

H1H2 H3

∂q1

∂q2

∂q3

A(1) H1

A(2) H2

A(3) H3

f = div grad f =

∑

∂

H1H2H3

∂f

H1H2H3 i

∂q

A = grad(div A) − rot(rot A).

Ці формули можна вивести, використовуючи векторні тотожності (див. задачі 9.23–9.25 і вказівки до них).

Зручність використання конкретної криволінійної системи координат (порівняно із декартовою) у певній задачі визначається особливостями геометрії відповідних полів. Наприклад, центрально-симетричне поле у координатах (х, у, z) має вигляд

A(x, y, z) = (xex + yey + zez ) f (r)/r (три компоненти), тоді як у

сферичних координатах (r, θ, ϕ): A(r,θ,ϕ) = er f (r) (одна ком-

понента). Відповідно зменшується кількість доданків у виразах для ротора та дивергенції такого поля, яка визначається кількістю відмінних від нуля його компонент.

У задачах 9.43–9.48 записані в інваріантному вигляді диференціальні вирази за участю оператора можна обчислити, викори-

3	3
стовуючи інваріантні подання A = ∑ A(i)e(i) ,	t = ∑ t(ij)e(i) e( j)
i=1	i, j=1

і формули диференціювання векторів фізичного базисуe(i) (див.

задачу 9.28). Більш універсальний підхід – використання апарату коваріантного диференціювання із переходом до фізичного базису лише у кінцевих виразах. Операція коваріантного диференціювання вводиться у криволінійних координатах як інваріантна диференціальна операція, у результаті якої із довільного тензора рангу n утворюється тензор рангу n+1. Наприклад, коваріантна похідна від коваріантного вектора –

a j,k = ∂∂qakj −aiΓijk , коваріантна похідна від контраваріантного

вектора – a

∂a j

, коваріантна похідна від двічі контра-

∂qk

+ a

∂tij

∂e

tij

+tljΓi

+til Γj

Γi

= ei

варіантного тензора –

, де

–

∂qk

символи Крістоффеля. Усі диференціальні векторні операції ви-

ражаються через коваріантну похідну, наприклад, grad u = u				ei ,
			,i
(a )b = a jb	ei , div A= Ai , диференціал векторного поля A = Aie
i, j		,i		i
має вигляд dA = Ai		dq je . Через	коваріантні похідні можна по-
	, j	i

дати також вираз для тензора деформацій (див. задачу 9.31).

9.18. Записати кінетичну енергію точкової частинки масою m, яку задано виразом T = mr 2 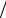2 , де r = r (t), у циліндричній, сферичній і параболічній системах координат.

9.19.Записати кінетичну енергію точкової частинки масою m,

яку задано виразом T = mr 2 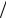2 , де r = r (t), у довільній ортогональній криволінійній системі координат.

9.20.Записати компоненти векторів швидкості v = r і приско-

рення a = r точкової частинки у циліндричній системі координат.

9.21.Записати компоненти векторів швидкості v = r і прискорення a = r точкової частинки у сферичній системі координат.

9.22.Записати компоненти векторів швидкості v = r і при-

скорення a = r частинки у довільній ортогональній криволінійній системі координат.

9.23. Довести формулу для f (r ) в ортогональній криволі-

3	∂f		3	1	∂f
нійній системі координат f = ∑ei		= ∑				e(i).
	i				i
i=1	∂q		i=1	Hi ∂q
9.24. Знайти rot e(i) в ортогональній			криволінійній системі

координат rot e(1) =

вести формулу для

1 e(2)

H1 H3 rot A(r )


			e				1	( H1 ×e(1) ) , до-
∂H1		−	(3)	∂H1		≡	1
∂H1		−		∂H1		≡
∂q	3		H2 ∂q		2		H1
∂q			H2 ∂q				H1

9.25. Знайти div e(i)

ортогональній криволінійній

системі

координат div e(1) =

∂H

, довести

формулу

∂q

для div A(r ) .

9.26. Знайти e(i) у циліндричній системі координат.

9.27. Знайти e(i) у сферичній системі координат.

9.28. Довести формулу

∂e(i)

e( j)

∂H j

−δij Hi та обчисли-

∂q j

∂qi

ти похідні від векторів фізичного базису для циліндричної і сферичної системи координат.

9.29. Симетричний тензор деформацій визначає зміну відстані між нескінченно близькими точками за деформації пружного

середовища, що задається полем зміщень u, а саме, якщо l – вектор, проведений з однієї точки до іншої, то в лінійному на-

	δl		3
ближенні за полем зміщень	δl	=	∑ u(ij)s(i)s( j) , де	s = l	l	.
	l		i, j=1		l
			i, j=1

У декартовій системі координат компоненти тензора деформацій

мають вигляд u	=	1	∂ui			+	∂u j	. Записати компоненти тензора
ij		2		∂x	j		∂x
					j		i

деформацій у циліндричній системі координат.

9.30. Записати компоненти тензора деформацій u(ij) у сфери-

чній системі координат (див. задачу 9.29).

9.31. Записати компоненти тензора деформацій u(ij) у довільній ортогональнійкриволінійній системі координат (див. задачу 9.29).

9.32.Записати оператор Лапласа у системі координат, яку задано рівняннями

x= (a + r cos θ)cos ϕ, y = (a + r cos θ)sin ϕ, z = r sin θ, де a = const.

9.33.Виразити похідні ∂∂x , ∂∂y , ∂∂z через циліндричні коорди-

нати (ρ,ϕ, z) та похідні ∂ρ∂ , ∂ϕ∂ , ∂∂z .

∂

9.34. а) Записати диференціальні оператори

Lx = y

∂z

− z

∂y

∂

Ly = z

∂x

− x

∂z

, Lz = x

∂y

− y

∂x

у циліндричних

координатах

(ρ, ϕ, z);

б) Записати векторний оператор

у циліндри-

L =[r × ]

чній системі координат і знайти його проекції на декартові орти. Порівняти відповідь із результатами п. а).

∂

9.35. Виразити похідні

через сферичні координа-

∂x

∂y

∂z

ти (r,θ,ϕ)

∂

та похідні

∂r

∂θ

∂ϕ

∂

9.36. а) Записати диференціальні оператори Lx = y

∂z

− z

∂y

∂

у сферичних координатах (r,θ,ϕ);

Ly = z

∂x

− x

∂z

, Lz = x

∂y

− y

∂x

б) Записати векторний оператор

L =[r × ] у сферичній системі

координат і знайти його проекції на декартові орти. Порівняти відповідь з результатами п. а).

9.37. Записати циклічні компоненти вектора у циліндричних і сферичних координатах (див. задачі 3.13, 3.14).

У задачах 9.38–9.40 записати оператор Лапласа від скалярної функції f (r ):

9.38.…у довільній криволінійній системі координат.

9.39.…у циліндричних і сферичних координатах.

9.40.…у параболічній системі координат.

У задачах 9.41–9.42 записати оператор Лапласа від векторної функції A(r ):

9.41.…у циліндричних координатах.

9.42.…у сферичних координатах.

У задачах 9.43–9.44 записати вектор ( A ) A:

9.43*. … у циліндричних координатах.

9.44*. … у сферичних координатах.

Дивергенція симетричного тензора другого рангу t у декартових

координатах має компоненти ( t)i = ∂tki . У задачах 9.45–9.46 знайти
компоненти вектора t:	∂xk
компоненти вектора t:
9.45*. … у циліндричних координатах.
9.46*. … у сферичних координатах.
Величина (t )u, t – симетричний тензор другого рангу,						u – век-
тор, у декартових координатах	обчислюється	як t	∂ui	.	У	задачах
тор, у декартових координатах	обчислюється	як t		.	У	задачах
		ij ∂x j
9.47–9.48 знайти вираз для обчислення величини (t )u:
9.47*. …у циліндричних координатах.
9.48*. …у сферичних координатах.
9.49. Записати рівняння Максвелла (у системі СІ):
rot E(r ,t) = − ∂B(r ,t) ,	rot H (r ,t) =	∂D(r ,t) + j			(r ,t) ,
∂t		∂t
div D(r ,t) = ρ(r ,t) ,	div B(r ,t) = 0 ,

уциліндричній і сферичній системах координат.

9.50.Обчислити, використовуючи циліндричні або сферичні координати та локальний базис (тут a = const ):

а) div r ;

б) rot r ;

в) (r a );

г) (a )r ;

д) div( f (r) r );

є) rot ( f (r) r );

r a

a r

ж)

;

з) div

;

і) rot

9.51. Обчислити f (r ), використовуючи

циліндричні або

сферичні координати та локальний базис, якщо

а) f (r ) = 1 r , б) f (r ) = eik r ,

в) f (r ) = eikr

r ,

де k = const .

9.52. Обчислити у сферичних координатах

(

)

aeikr

б)

aeikr

в)

rot

aeik r

а) div

;

rot

;

де a та k

– сталі вектори, k =

9.53. Обчислити в циліндричних координатах:

(ρ

ϕ),

cosϕ

а)

+ 2ρcosϕ−e

sin

б) rot

sin ϕeρ

eϕ −ρz ez

div(ρeρ + zsin ϕeϕ +e

cos z ez ),

sin

в)

г) rot cosϕeρ

−

eϕ

+ρ

ez .

9.54. Обчислити у сферичних координатах:

а) (r

sin θ),

αcos θ

б)

в) div 2cos θe

+ sin θe

г) rot

2cos θe

+ sin θe

3 θ

9.55. Знайти потенціал векторного поля A = 2cosθe + sin θe .

9.56.Знайти потенціал векторного поля A = ρeρ + ϕρ eϕ + zez .

9.57.У сферичній системі координат знайти потенціал векто-r θ

рного поля A = θer +eθ . 9.58. Довести, що

2	r ,	у просторі,	де r =	r	.
r =	r ,		де r =	r	.
1	r ,	на площині,
9.59. Обчислити	rm	у сферичних координатах. Знайти час-

тинний розв'язок рівняння Δϕ = 1/r .

Розділ 10 Інтегральні теореми

Інтеграл від функції однієї змінної має відому властивість

b	d	(10.1)
∫ dx f (x) dx = f (b) − f (a),		(10.1)
∫ dx f (x) dx = f (b) − f (a),
a

іншими словами: інтеграл від повного диференціала функції df на інтервалі [a, b] визначається тільки значеннями функції f на її межах. Інтегральні теореми Остроградського–Гаусса та Стокса узагальнюють цей факт на випадок об'ємних і поверхневих інтегралів.

Для векторних функцій векторного аргументу існує кілька комбінацій із диференціальним оператором , які можна роз-

глядати як узагальнення повної похідної у лівій частині (10.1). Відповідні співвідношення називаються інтегральними теоремами.

У курсі математичного аналізу доводять теореми Остро- градського–Гаусса та Стокса, які можна сформулювати наступним чином.

Теорема ОстроградськогоГаусса. Нехай в об'ємі V, обме-

женому замкненою поверхнею S(V), задано неперервно диференційовну векторну функцію A(r ) , яка є неперервною у замкненій області, включно із поверхнею S. Тоді має місце рівність

∫div A(r ) dV =	∫ A(r ) n(r ) dS.	(10.2)
V	S (V )

Тут і далі використовуються позначення: n(r ) – вектор зовнішньої нормалі до поверхні S у точці r , вектор n dS = dS – век-

торний елемент площі на поверхні S. Рівність (10.2) означає, що інтеграл у лівій частині визначається тільки через граничне зна-

чення функції A(r ) на поверхні S(V). Для функцій, умови непе-

рервності яких порушено, теорема Остроградського–Гаусса може не виконуватись. Підкреслимо, що неперервність функції вимагається у замкненій області, включно із поверхнею S, а існування та неперервність частинних похідних – тільки у внутрішніх точках об'єму V. Подібні за суттю вимоги неперервності існують для всіх

інтегральних теорем. Фізичний зміст (10.2) визначається у контексті гідродинаміки та класичної електродинаміки, інтеграл у

правій частині описує потік векторного поля A(r ) (поля швидко-

стей рідини, електричного поля тощо) через поверхню. У поля із нульовою дивергенцією відсутні джерела в об'ємі V, тоді потік

вектора A(r ) через поверхню S дорівнює нулю.

Теорема Стокса. Нехай задано замкнений контур L, поверхню S, яка спирається на контур L, і неперервно диференційовну

на поверхні S векторну функцію	A(r), що є неперервною на S,
включно із межею L. Тоді має місце співвідношення
∫rot A(r ) n(r ) dS =	∫ A(r ) τ(r ) dl.	(10.3)
S	L(S )

Тут і далі використовуватимемо позначення: τ(r ) – одиничний направляючий вектор на кривій L у точці r (вектор дотичної) у напрямку обходу кривої L, dl = τdl – векторний елемент довжини вздовж контуру. Вибір напрямку нормалі n(r ) до поверхні у точ-

ці r у (10.3) узгоджується із напрямком обходу контуру, який тут і в наступних прикладах вважатимемо вибраним додатним щодо n(r ). Інтеграл у правій частині (10.3) називають циркуляцією век-

торного	поля A вздовж замкненого контуру L. У випадку
rot A = 0	циркуляція зникає (фізичною ілюстрацією може служи-

ти рівна нулю робота потенціальної сили F у результаті перемі-

щення точки вздовж замкненої траєкторії, тобто циркуляція F вздовж контуру).

Із цих основних форм інтегральних теорем можна отримати низку інших, які відрізняються способом множення операто-

ра і типом функції, на яку він діє, під знаком інтеграла. Вони наведені у задачах 10.1 та 10.2 (див. також вказівки до них). Різні формулювання інтегральних теорем можна записати у компактній формі, зручній у практичних застосуваннях – їх наведено в тексті після задач 10.1 та 10.2.

10.1. Довести інтегральні теореми, що є наслідками теореми Остроградського–Гаусса:

а)

∫

ϕndS = ∫ ϕdV ;

б)

∫

(n )ϕdS = ∫ ΔϕdV ;

S(V )

в)

∫

n × AdS = ∫ rot AdV ;

г)

∫

(n ) AdS = ∫ AdV ;

S (V )

д)

∫

n t

dS =

∫

∂tij

dV ,

xi , t

− декартовікомпоненти.

∂xi

S (V )

Інтегральні теореми типу а)–д) можна записати у вигляді загального правила ∫ n (…)dS = ∫ (…)dV , де (…) – означає один і той

S (V )	V
самий об'єкт (будь-який),	а – будь-який допустимий для нього тип

множення, також один і той самий ліворуч і праворуч.

10.2. Довести інтегральні теореми, що є наслідками теореми Стокса: а) ∫ ϕτdl = ∫(n × )ϕdS; б) ∫ (τ )ϕdl = 0;

L(S )	S	L(S )
в) ∫ (τ× A) dl = ∫((n × ) × A)dS.
L(S )		S

Інтегральні теореми типу а)–в) можна записати у вигляді загального правила ∫ τ (…)dl = ∫(n × ) (…)dS, де (…) – означає один і

L(S ) S

той самий об'єкт (будь-який), а – будь-який допустимий для нього тип множення, також один і той самий ліворуч і праворуч.

10.3. Поверхневийінтеграл ∫ Δϕ∂ϕ∂n dS перетворитинаоб'ємний.

	S(V)
10.4. Об'ємний	інтеграл ∫ ϕ rot AdV перетворити на по-
верхневий.	V
верхневий.			а) ∫ r (a n )dS;
10.5. Обчислити	поверхневі	інтеграли:	а) ∫ r (a n )dS;
			S (V )
б) ∫ n(a r ) dS; в) ∫ a(n r ) dS; г) ∫ r ×(n ×a) f (r) dS;
S (V )	S (V )	S (V )

д) ∫ (n ×b) (a ×r ) dS; де a та b – сталі вектори.

S (V )

<<< < Предыдущая 1 2 3 4 5 6 78 / 148 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.09.2019276.26 Кб3otvety_na_ekzamen_s_adminki (1).docx
#
17.12.20182.31 Mб4Otvety_na_voprosy_k_ekzamenu_po_teoreticheskim.doc
#
09.11.2019744.96 Кб5overview_american.doc
#
09.11.20191.26 Mб14overview_British.doc
#
19.03.20151.67 Mб46ovta-posibnyk.pdf
#
07.03.20161.46 Mб28ovta-zbirnyk-zadach.pdf
#
19.03.20152.57 Mб1623O_M_Pazyak_O_A_Serbenska_M_I_Furduy_L_Yu.doc
#
15.11.2019261.12 Кб1Palestina-95 Later edited.doc
#
11.09.2019112.64 Кб6paronimi.doc
#
28.07.201926.2 Кб2Part 1.docx
#
07.03.20162.26 Mб37patology.pdf