Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Киевский национальный университет им. Т. Шевченко

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ovta-zbirnyk-zadach

.pdf

Скачиваний:

Добавлен:

07.03.2016

Размер:

1.46 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1412 13 14 > Следующая >>>

7.14. Указівка:

mr = αr r3

7.13. Указівка:

x(t) = C1et ,

7.2. а) (a,b,c) +(a,b,c) +(a,b,c) ; б) a ×(b ×c) +a ×(b ×c) +a ×(b ×c).

7.6.Указівка: для доведення другого твердження скористатися результатом задачі 7.4.

7.7.Указівка: вектор прискорення r є паралельним до вектора r ,

тобто r × r = 0, якщо	d	(r ×r ) = 0, тоді r ×r = const,	і траєкто-
	dt

рією руху є плоска крива; розв'язати рівняння r = β2 r			у площи-

ні z=0 та отримати знаконевизначену квадратичну форму, яка задає рівняння гіперболи.

7.8. ϕ(t) =1/(at +b) , a,b = const. Указівка: для прямої [r × r ]z = 0.

7.9. Якщо напрям r є незмінним. Контрприклад: r						= (cost,sin t) ,
	r	= 1,	d	r	= 0.
			d
			dt
			dt
7.10. Траєкторіями є кола, утворені перетином сфер							r 2 = C12 із
площинами					(r a) = C2 . Задача відповідає руху	в	просторі

швидкостей зарядженої частинки в однорідному постійному магнітному полі. Інтегралами руху є кінетична енергія та проекція імпульсу на напрямок магнітного поля.

7.11. У декартовій системі координат, де Oz n :

y(t) = C2 et , z(t) = C3 , де Ci = const . Траєкторіями є прямі, що перетинають вісь Oz під прямим кутом.

подати вектор швидкості у вигляді r = vn, де n –

одиничний вектор, та отримати із рівняння Ньютона, що n = 0. рівняння Ньютона помножити вектор-

но на r і на L = mr × r , скористатись результатом задачі 7.1 ж), та отримати векторні інтеграли руху L та A = α(r r )+ r × L.

Траєкторіями є гіперболи, еліпси або параболи, що лежать у площині r L = 0, напрям на перигелій указує вектор A. Рівняння траєкторії у циліндричній системі координат, пов'язаній із L

та A: ρ =	L2 / m	.
	Acos ϕ − α

111

Диференціальні операції над скалярними та векторними функціями

8.3. div(ϕA) = (ϕA) = (ϕA + ϕA) =

=ϕ A + ϕ( A) = A ϕ + ϕdiv A

8.7.( A B) = ( A B) = ( A B) + ( A B) . Для зміни порядку множників у кожному із доданків скористаємося формулою для подвійного векторного добутку у вигляді b(a c) = a ×(b ×c) +(a b)c .

Тоді ( A B) = (B A) = B ×( × A) +(B ) A = B ×rot A +(B ) A,( A B) = A × ( × B) + ( A )B = A × rot B + ( A )B .

Додаючи отримані рівності, знайдемо

( A B) = A rot B + B rot A + ( A ) B + ( B ) A .

8.17.div A .

8.21. а) r 2 = ( x2 + y2 + z2 ) = 2( xex + yey + zez ) ≡ 2r . З іншого

боку, r 2 = 2r r,

звідки r = r/r.

Другий спосіб

r =

+ y

+ z

xex + yey + zez

≡

;

x2 + y2 + z2

∂

б) (a r ) = ex

+ ey

+ ez

( xax + yay + zaz ) =

∂x

∂y

∂z

= ax ex + a y ey + az ez ≡ a;

в) nrn−2r ; г)

(a r )r

+ ra; д) −

αr

; є)

;

r 2

∂

ж)

(a )r = ax

+ a y

+ az

( xex + yey + zez ) =

∂x

∂y

∂z

= ax ex + a y ey + az ez ≡ a .

Зауважимо, що у цьому випадку вектор a може бути змінним.

з) a(r b ) + b(r a) ; і) f (r)a +	(a r )r	f ′(r) ;
	r

к) 2a2r − 2a(a r ) ; л) 2a(a r ) ; м) r 2 a − 3(a r )r . r5

112

8.22. а) 3, 0;

б) 5r2, 0; в) (n + 3)rn, 0; г) 2/r, 0; д) 0, 0; є)

(3 − n)r −n ,

0; ж) 0,

2a ; з)

div(r(a r)) = (a r)divr + r (a r) = 3(a r) + r a = 4(a r) ,

де використано "елементарні"

похідні

div r = 3,

(a r ) = a ;

rot(r (a r )) = a r ;

і)

(a b ) , −a ×b ;

к)

nrn−2(a r) ,

nr n−2 (r × a);

л) 2(a b) , −a b ; м) −2(a r ), 3r ×a ; н) 0 , (−r 2 a + 3(a r )r )/r5 ;

о) a r

, r ×a

п) 0, 3ra −

(a r )r

8.23.

≡ r

а)

ϕ′

;

′

)

′

(r) =

(r) r

(r)

б)

× A (r) .

A(r) ;

8.24.

а) ϕ(r)a + r r ϕ′(r)(a r ) ;

б)

a A(r) + (a r )(r r A′(r));

в)

′

г)

A(r) × a + ( A′(r), a, r )

;

a ×A(r) +(a r )( r

× A (r)) ;

д) 2(a A(r)) + (ra − (a r ) r r ) A′(r) ; є) a ×(A(r) +(r A′(r)) r r ).

8.25. а)

ϕ′′(r) +

ϕ′(r) ; б)

ϕ′′(r)

; в) A′′(r) +

A′(r) ; г) n(n −3)(a r)r−n−2 .

ikr

г) (a

+ik(r a))eik r ;

8.26. а)

ik eik r ;

б)

eikr;

в)

(ikr −1)r

eikr ;

д)

ik r

;

ik r

;

ж)

ik r r

A′(r)

+ ik

;

i(k a)e

є)

i(k ×a)e

A(r)

з) ikr −1(a r)eikr ; r3

л)

− 2i(k r ) + k2r2 eik r ; r3

і)

ikr −1

(

r ×a

)

eikr

;

к) −

ik r

;

2ik

ikr

м)

− k

8.27. с/r3, де c = const.

r ×(a × r )

8.28. с/r, де c = const.

8.29. 0;

2ϕ(r) a + ϕ′(r)

. 8.30.

p −

A .

8.31. a) (a ) ϕ,

2mc

б) ϕgrad(div A) + grad ϕdiv A +

+(grad ϕ ) A + ( A ) grad ϕ + grad ϕ× rot A.

8.32. a)

′

б) 0;

′

3ϕ(r) + rϕ

(r) ;

в) ϕ(r)a + ϕ

(r)(a r )(r / r).

8.33. 1

−

ϕ′(r)

ϕ′′(r)

r × (r × a ) − 2a

113

′

r);

′

8.34. a) A(r) + (r A (r))(r

б) ( A

(r) B(r) + A(r) B

(r))(r r);

в)

(ϕ(r)(r

′

г)

ϕ(r)

′

(r)

× A(r);

A'(r)) +ϕ (r)(r A))/r;

× A

(r) + ϕ

д) a r r ϕ′(r); є) a r r (ϕ′(r) A(r) + ϕ(r) A′(r));

ж) 0;

з) ϕ′(r) + 2

ϕ(r); і) r × a

3 ; к) (A′(r) ×(r ×a))

r .

8.35.a) 2a2 ; б) 4a2 ; в) −2a .

8.36.a) ddfϕ f ; б) dAdf f ; в) f × dAdf .

8.37. a) u u + (grad u)2 , б) u v + grad u grad v.
8.38. div v = 0, rot v = 2ω; div a = −2ω2 ,			rot a = 2ε.
8.39. −∫ rϕ(r) dr + c, де c = const .
8.40. F = − Φ(r) = −	d Φ(r)	er = F (r )er ,	Φ(r) = −∫ F(r)dr.

	dr

8.41. F = ϕ(ρ)ρ/ρ = − Φ;	Φ = −∫ ϕ(ρ) d ρ , де ρ = xi + yj.
	n	γmi
8.42. ϕ(r ) = −γm r .	8.43. ϕ(r ) = −∑		.
		r − r

	i=1	i

8.44. Указівка: обчислити div A . 8.45. ϕ(r) = c/r3, де c = const, r ≠ 0.

8.46.Указівка: обчислити rot A .

8.47.Указівка: див. указівку до задачі 8.44.

8.49.Указівка: спростити вираз (r × )2 u(r ).

8.50.Указівка: виконати операцію rot від обох частин рівняння

рівноваги рідини і скалярно помножити на f .

Π r

4πμ ∂j

με ∂2 E

8.51. A = 4π

8.52.

E − div E −

− c2

∂t2 = 0,

c2 ∂t

H − div H +

4π rot j − εμ ∂2 H = 0 .

4π

∂t2

8.53.

A = −

j ,

ϕ = −4πρ , де

–

оператор

д'Аламбера,

≡

−

∂2

∂t 2

8.54. Указівка: скористатись результатом задачі 8.52.

114

8.56. E = E0 e−k2 r ei(k1 r −ωt ) , H = H 0 e−k2 r ei(k1 r −ωt) , де

4πσ

1/2

4πσ

1/2

k = ω με

, k

= ω με

−1 ,

c 2

εωcosθ

θ = (k1, k2 ) .

8.58.Φ = ∂ϕ + v2 . ∂t 2

Указівка: якщо врахувати формулу v2 = 2(v )v + 2v ×rot v (див. задачу 8.8), то поле прискорень можна записати у вигляді

∂v

−v ×rot v. Оскільки v = ϕ, то

∂

ϕ+

v2,

∂t

звідки знаходимо відповідний потенціал.

Векторний аналіз у криволінійних координатах

Криволінійні ортогональні координати

9.1. а) Hρ = 1 , H ϕ = ρ , H z = 1 . Приклад обчислення:

∂r	=	∂(ρcos ϕ) ex +				∂(ρsin ϕ) ey +	∂z	ez = cos ϕex + sin ϕey ,
∂ρ	=	∂(ρcos ϕ) ex +				∂(ρsin ϕ) ey +	∂ρ	ez = cos ϕex + sin ϕey ,
∂ρ				∂ρ		∂ρ	∂ρ
звідки H		ρ	=	∂r	= 1 ;
звідки H			=	∂r	= 1 ;
				∂ρ

б)	eρ = ex cos ϕ + e y sin ϕ,		eϕ = −ex sin ϕ + ey cos ϕ,	ez = ez ;
в)	ax	= aρ cos ϕ − aϕ sin ϕ,	ay = aρ sin ϕ + aϕ cos ϕ,	az = az ;
г)	ρ =	x2 + y2 = const –циліндр, tgϕ = y x = const –		напівплощи-

на, що утворює кут ϕ із площиною xOz та обмежена віссю Oz, z = const – площина.

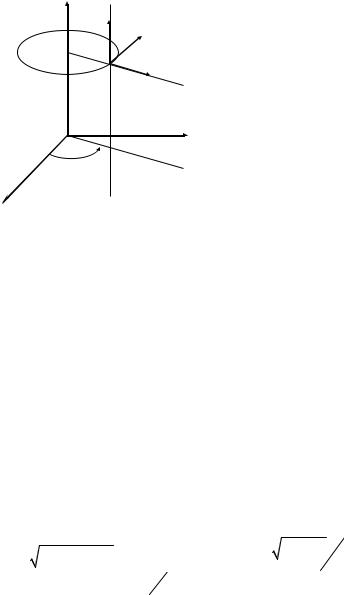
Через кожну точку проходять три координатні лінії, які можна розглядати як результат перетину відповідних координатних поверхонь: коло (ϕ-лінія, уздовж якої ϕ змінюється у межах від 0 до 2π, ρ і z –фіксовані), напівпряма (ρ – лінія, уздовж якої ρ змінюється у межах від 0 до +∞, ϕ і z – фіксовані), пряма (z-лінія, уздовж якої z змінюється в межах від –∞ до +∞, ϕ і ρ – фіксовані);

115


		д) вектори локального базису
z	eGz	та	параметри			Ламе	можна
		знайти геометрично, не кори-
	eGϕ	стуючись прямокутною дека-
	eGρ	ртовою системою координат.
ϕ-лінія		Візьмемо			довільну		точку
		M (ρ0 , ϕ0 , z0 ) (див. до рис. 9.1).
	ρ-лінія
		Зафіксуємо ϕ, z, змінювати-
		мемо		ρ.	Тоді	радіус-вектор
ϕ	у	r =r(ρ, ϕ0, z0) опише ρ-коорди-
		натну лінію. Аналогічно отри-
		мують ϕ-, z-координатні лінії,
x	z-лінія	і,	таким		чином	через	кожну
		точку		можна		провести три
до задачі. 9.1
		різні координатні лінії.

Якщо ми надаємо приріст радіус-вектору r =r(ρ, ϕ, z) за ρ-ко-

ординатною лінією Δρ, то величина	∂r	=	lim	r	=	lim	Δρρ	=	ρ	=e
	∂ρ		Δρ→0	Δρ		Δρ→0	Δρρ		ρ	ρ

– вектор, дотичний до ρ-координатної лінії, а його довжина Нρ=1.

Якщо ми надаємо приріст радіус-вектору			r =r(ρ, ϕ, z) за ϕ-ко-
ординатною лінією Δφ, то величина	∂r	= lim		r	= lim	ρΔϕeϕ	=ρe

	∂ϕ	Δϕ→0 Δϕ Δϕ→0				Δϕ	ϕ

– вектор, дотичний доϕ-координатної лінії, айогодовжина Нϕ=ρ.

9.2. а) Нr = 1, Нθ = r, Нϕ = rsinθ;

б) er = ex sin θcos ϕ+ ey sin θsin ϕ+ ez cos θ,

eθ = ex cosθcosϕ+ey cosθsinϕ−ez sinθ, eϕ = −ex sinϕ+ey cosϕ; в) ax = ar sin θcos ϕ+ aθ cos θcos ϕ− aϕ sin ϕ,

ay = ar sin θsin ϕ+ aθ cos θsin ϕ+ aϕ cos ϕ, az = ar cos θ−aθ sin θ;

г) r = x2 + y2 + z2	= const – сфера, tg θ = x2 + y2			z = const –
конічна поверхня,	tgϕ =	y	= const – напівплощина, що утворює
		x
			116

кут ϕ (0 ≤ ϕ < 2π) із площиною xOz та обмежена віссю Oz. Через кожну точку із координатами r, θ, ϕ проходить три координатні лінії: коло (ϕ-лінія, вздовж якої ϕ змінюється у межах від 0 до 2π, r і θ – фіксовані), напівпряма (r-лінія, уздовж якої r змінюється у межах від 0 до +∞, ϕ і θ – фіксовані), напівколо (θ-лінія, вздовж якої θ змінюється у межах від 0 до π, а ϕ і r – фіксовані).

	z		r-лінія
		eGr
		eGϕ
ϕ-лінія	θ	eGθ
	θ	eGθ	y
			y
	ϕ
		θ-лінія
x		до задачі. 9.2
		до задачі. 9.2

9.3. а) H u = H v = u 2 + v2 , Hϕ = uv;

б) eu =

ev =

в) ax =

ay =

1	(v(ex cos ϕ + ey sin ϕ) + uez ),
u 2 + v2	(v(ex cos ϕ + ey sin ϕ) + uez ),
u 2 + v2	(u(ex cos ϕ + ey sin ϕ) − vez ) , eϕ = −ex sinϕ+ey cosϕ;
1
u 2 + v2
u 2 + v2
v cos ϕ	au +	u cos ϕ	av − sin ϕaϕ;
u2 + v2	au +	u2 + v2	av − sin ϕaϕ;
u2 + v2		u2 + v2		−vav +uau
v sin ϕ	au +	u sin ϕ	av + cos ϕaϕ; az =	−vav +uau	;
u 2 + v2	au +	u 2 + v2	av + cos ϕaϕ; az =		;
u 2 + v2		u 2 + v2		u2 + v2

г) y x = tg ϕ = const –	напівплощина,	що утворює кут	ϕ
(0 ≤ ϕ < 2π) із площиною xOz та		обмежена віссю	Oz,
x2 + y2 + z2 ± z = const	– параболоїди. Через кожну точку із ко-

координатами u, v, ϕ проходить три координатні лінії: коло (ϕ-лі- нія, уздовж якої ϕ змінюється у межах від 0 до 2π, u та v – фіксовані) та дві напівпараболи, які є результатом перетину координатних поверхонь (напівплощини і відповідного параболоїда).

9.4. H ξ = H η =	a	,	H α =		a sin η	.
	ch ξ − cos η				ch ξ − cos η

9.5. Hρ = H ξ =	a	,	H α =		a sh ρ	.
	ch ρ − cos ξ			ch ρ − cos ξ

			117

9.6. e

= eiϕ (e

+ ie

), e = e−iϕ(e −ie ),

= k .

−

9.7. e+ = eiϕ (sin θer

+ cos θeθ ) + ieiϕeϕ ,

−

= e−iϕ (sin θe

+ cos θe

) − ie−iϕ e

= cos θe

−sin θe .

9.8. txx = tρρ cos2 ϕ − 2tρϕ sin ϕcos ϕ + tϕϕ sin 2 ϕ,

txy

= tρρ sin ϕcos ϕ + tρϕ (cos2 ϕ − sin 2 ϕ) − tϕϕ sin ϕcos ϕ,

txz

= tρz cos ϕ − tϕz sin ϕ,

t yy

= tρρ sin 2 ϕ + 2tρϕ sin ϕcos ϕ + tϕϕ cos2 ϕ,

t yz

= tρz sin ϕ + tϕz cos ϕ,

tzz = tzz .

9.9.

ρeρ + zez

9.10. ρsin 2ϕ+ρcos 2ϕ.

9.11. ρz(eρ −ez ).

ρ2 + z 2

9.12. r 2 sin 2ϕcos 2θ.

9.13. sin θeϕ.

9.14.ρ = cϕ, c = const (спіраль Архімеда).

9.15.ϕ = C1, r = 2sin θ+C2. Векторні лінії утворюються перетином двох сімейств поверхонь.

9.16.

−2

= −ln

+ C1,

tg θ = C 2.

9.17. Промені, які виходять із точки розташування заряду.

Диференціальні операції у криволінійних координатах

9.18.а) T = m2(ρ2 +ρ2ϕ2 + z2 ); б) T = m2(r2 +r2θ2 +r2 sin2 θϕ2) ; в) T = m 2 ((u2 + v2 )(u2 + v2 ) + u2v2ϕ2 ).

9.19.T = m 2 (H12 (q1 )2 + H 22 (q2 )2 + H32 (q3 )2 ).

9.20. v = ρe

+ρϕe

+ ze

, a = (ρ − ρϕ2 )e

1 d

(ρ2 ϕ)e

+ ze

ρ dt

9.21. v = rer

+ rθeθ + r sin θϕeϕ ,

a = (r − rθ2 − rϕ2 sin 2

θ) er + (rθ + 2rθ − rϕ2 sin θcos θ) eθ +

+ (rϕsin θ + 2rϕsin θ + 2rθϕcos θ) eϕ.

118

9.22. v = ∑Hiqie(i) ; i=1

3 e(i)

∂T

a =

∑

−

∂q

i=1

Hi dt ∂q

1 3 2

T = ∑ Hi2 (qi ) –

2 i=1

кінетична енергія частинки одиничної маси.

9.23. Указівка: для довільних dqi прирівняти диференціали

df = 3 ∂f dqi = dr f , записавши dr через фізичний базис.

∑i=1 ∂qi

9.24. Указівка: в ортогональній криволінійній системі координат використати результат задачі 9.23 у тотожності rot qi ≡ 0 .

9.25. Указівка: в ортогональній криволінійній системі координат використати результат задачі 9.24 у тотожності div e(1) = div(e(2) ×e(3) ).

9.26.

= −

, e

− 1

e ,

= 0.

ρ2

ρ2 ϕ

9.27.

= −

er ,

eθ = −

eθ −

ctg θer ,

eϕ = −

eϕ.

sin

9.28. Відмінні від нуля похідні: а) у циліндричній системі коор-

динат

∂eρ

= e

∂eϕ

= −e

;

б) у сферичній системі

координат

∂ϕ

∂eϕ

∂e

= e ,

= sin θe

= −e

= cos

θe

= −sin θe −cos θe .

∂θ

∂ϕ

∂θ

∂ϕ

Указівка: порівнюючи дві формули

∂g

∂e

∂g

Γij,l = 1 2

∑

−

∂q

= ∑ ek Γij = ∑ ek g

∂q

k =

k ,l

∂H j

= e

∂H

−δ

та

∂e

∂H

∂e(i)

= e

i + H

∂qi

∂q j

i ∂q j

(i) ∂q j

( j)

(i) ∂q j

знаходимо

∂e(i)

e( j)

∂H j

− δij Hi .

∂qi

∂q j

∂u

∂

∂u

9.29. u

∂uz

;

ρρ

∂ρ

ϕϕ

ρ ∂ϕ

∂z

ϕz

ρ ∂ϕ

∂z

2uρz =

∂uρ

∂u

2uρϕ

∂uϕ

−

uϕ

1 ∂uρ

∂z

∂ρ

ρ ∂ϕ

∂ρ

119

9.30. u

∂ur

, u

∂u

∂uϕ

∂r

θ +

, u

θ ctg θ+

r ,

rsin θ ∂ϕ

θθ

∂θ

ϕϕ

∂uϕ

∂uθ

2uθϕ =

−uϕ ctg θ

∂θ

r sin θ ∂ϕ

∂uϕ

uϕ

2urθ =

∂u

θ −

∂u

r ,

2uϕr =

∂u

r +

−

∂r

∂θ

r sin θ ∂ϕ

9.31. Відповідь:

1 ∂u(i)

1 ∂u( j)

u(ij ) =

−

∂q

+ δij H1i (u )Hi .

	∂H j			∂H
u( j)			+ u(i)		ji	+
	∂q	i		∂q

Указівка: із означення (див. задачу 9.29) маємо

δl	= s (s )u =	3	e(i)	∂	(u(k )e(k ) ) ,
		∑ s(i) s( j)
l			H j	j
		i, j,k =1		∂q

компоненти тензора деформацій зручно знаходити за формула-

ми u ij		=	1	(ω(ij) + ω( ji) ),	де ω(ij) =	1	∂u (i)
	)
								j
(			2				∂q
						H j

	3		∂e
	∑
	∑			j
+		u(k )e(i)	(k )		,
+		u(k )e(i)			,
	k =1		∂q

користуючись результатами задачі 9.28 для відповідних криволінійних систем; можна також використати представлення тензора деформацій через коваріантні похідні від вектора зміщень

= 1

j,i

+ u

i, j

)

та відповідні фізичні компоненти

uij

u(ij)

(ui, j

+ u j,i ) ,

Hi H j

2Hi H j

оскільки u

e i

e j =

uij

= u

Hi H j

(i)

( j)

(ij) (i)

( j)

∂

∂f

9.32.

r(a + r cos θ)

r(a

+ r cos θ) ∂r

∂r

∂

∂f

∂

+ r cos θ)

a + r cos θ ∂ϕ

∂θ

120

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1412 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.09.2019276.26 Кб3otvety_na_ekzamen_s_adminki (1).docx
#
17.12.20182.31 Mб4Otvety_na_voprosy_k_ekzamenu_po_teoreticheskim.doc
#
09.11.2019744.96 Кб5overview_american.doc
#
09.11.20191.26 Mб14overview_British.doc
#
19.03.20151.67 Mб46ovta-posibnyk.pdf
#
07.03.20161.46 Mб29ovta-zbirnyk-zadach.pdf
#
19.03.20152.57 Mб1623O_M_Pazyak_O_A_Serbenska_M_I_Furduy_L_Yu.doc
#
15.11.2019261.12 Кб1Palestina-95 Later edited.doc
#
11.09.2019112.64 Кб6paronimi.doc
#
28.07.201926.2 Кб2Part 1.docx
#
07.03.20162.26 Mб37patology.pdf