
ovta-zbirnyk-zadach
.pdfвеличини detA = ± 1). Якщо detA > 0 (див. задачу 2.1), то відповідне перетворення (2.1) системи координат є просторовим поворотом і переводить праву систему координат у праву, а ліву – у ліву (див. задачу 2.2). Якщо ж detA < 0, то перетворення (2.1) системи координат можна подати як послідовність деякого просторового повороту та дзеркального відображення у площині або інверсії, що переводить праву систему координат у ліву, а ліву – у праву.
Зауважимо, що декартові координати точки при переході від однієї прямокутної декартової системи координат до іншої перетворюються так само, як і базисні вектори (вирази (2.1) та (2.4), відповідно), а саме
xi′ = αij x j та xi = α ji x′j . |
(2.6) |
Для пошуку елементів матриці переходу можна скористатись будь-яким із співвідношень (2.1)–(2.6), а найбільш раціональний спосіб залежить від того, які саме величини задано.
Якщо відомо кути між осями двох систем координат (див. задачу 2.4), то елементи αij матриці переходу зручно шукати за (2.2) як косинуси відповідних кутів. Можна також виразити базисні вектори штрихованої системи координат як лінійні комбінації векторів нештрихованого базису, або навпаки. Згідно із (2.1) та (2.4), рядки матриці переходу – суть компоненти штрихованих базисних векторів у нештрихованому базисі (див. задачу 2.5), а стовпчики – компоненти нештрихованих базисних векторів відносно штрихованих (див. задачу 2.6).
2.1. Довести, що |
det A |
= 1. |
|
|
|
|
2.2. Довести, що |
(e′ |
,e′ |
,e′ ) = det A (e ,e ,e ) . |
|||
|
1 |
2 |
3 |
1 |
2 |
3 |
2.3. За заданими елементами матриці переходу відновити решту
|
1 |
|
|
|
|
|
|
|
α |
|
β |
|
|
|
|
|
||
1) |
|
|
|
|
|
; |
2) |
|
|
−1 |
|
, де α |
2 |
+β |
2 |
= 1; |
||
|
−1 |
|
|
|
|
|
||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3) |
|
|
|
α |
|
, |
|
α |
|
= 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
Для випадку 2) знайти визначник матриці переходу для обох варіантів вибору знаку α31. У чому полягає їх відмінність?
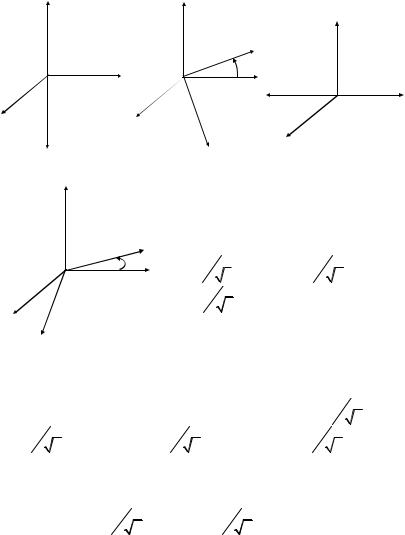
2.4. Знайти елементи матриць переходу для перетворень, по-
даних на рис. 2.2.–2.5.
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z, x' |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О |
|
|
|
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
y,y' |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
O |
|
|
y' |
|||||
|
x,z' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
x,z' |
|
|
|
|
|
|
|
|
|
|
|
|
x,z' |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x' |
|
|
|
|
|
|
|
|
|
|
|
|
y' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Рис. 2.2 |
|
|
|
|
|
Рис. 2.3 |
|
|
|
|
|
|
|
|
|
|
Рис. 2.4 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.5. |
Знайти матрицю |
переходу |
|||||||||||||||||||
|
|
|
|
|
|
|
|
z,z' |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
від системи координат S до S', якщо |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
базисні вектори |
ei |
|
(де |
i = 1, 2,3 ) |
у |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
системі S' |
мають |
|
координати |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x' |
|
|||||||||||||||||||||||
|
|
|
|
|
O |
|
|
|
α |
|
|
|
|
|
e |
= |
1 |
|
|
(1,1,1) , |
e |
|
= |
1 |
|
|
|
(1,0, −1) , |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
1 |
|
1 |
3 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
= |
(−1,2, −1) . |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.6. Знайти |
матрицю |
переходу |
|||||||||||||||||||
|
|
|
|
|
y' |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
від базису i , |
j, |
k |
до базису, що за- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
Рис. 2.5 |
|
|
|
|
|
||||||||||||||||||||||||
даний векторами e1′ = (0,α,β) , |
e2′ = (1,0,0) , |
e3′ = (0,β, −α) , якщо |
|||||||||||||||||||||||||||||||||||
α2 + β2 = 1. |
|
|
|
|
|
|
|
|
|
e = (1,0,0), |
|
|
|
1 |
|
|
|
|
|
|
|||||||||||||||||
|
|
2.7. У ПДСК задано вектори |
|
e |
= |
|
|
(0,1,1), |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
||
e3 |
= 1 |
|
|
|
|
|
|
|
|
e1′ = |
1 |
|
|
|
|
|
|
|
|
e2′ = |
1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
(0,1, −1), |
|
2 |
(1, −1,0) , |
|
2 |
(−1, −1,0) , |
||||||||||||||||||||||||||||
e3′ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= (0,0,1) . Знайти матрицю переходу від базису ei |
до базису |
||||||||||||||||||||||||||||||||||||
ei′ ( i = 1, 2,3 ).
2.8. Знайти матрицю переходу від системи координат S до S',
якщо x |
′ |
= z , |
y |
′ |
= |
1 |
2 (x − y) , |
z |
′ |
= |
1 |
(x + y) . |
|
|
|
|
2 |
||||||||
|
|
|
|
|
|
|
|
22 |
|
|
||
2.9. Подати зображення взаємного розташування систем координат, пов'язаних матрицями переходу
|
0 |
0 |
1 |
|
|
0 |
0 |
1 |
|
|
1 |
0 |
0 |
|
|
0 |
−1 0 |
|
|
а) |
; |
б) |
. |
||||||
|
0 |
1 |
0 |
|
|
1 |
0 |
0 |
|
|
|
|
|
||||||
2.10. Знайти матриці переходу для перетворень: а) поворот на кут π навколо осі Ох; б) дзеркальне відображення у площині уОz; в) інверсія.
2.11.Показати, що поворот на кут π із наступним дзеркальним відображенням у площині, перпендикулярній осі обертання, еквівалентний інверсії.
2.12.Знайти матриці переходу для поворотів системи коор-
динат на кут α (проти годинникової стрілки): а) навколо осі Ох; б) навколо осі Оу; в) навколо осі Оz. Переконатись, що матриця переходу для повороту на кут (–α) (тобто перетворення, оберненого до даного) збігається із транспонованою матрицею.
2.13.Знайти матрицю переходу для повороту на кут ϕ навколо осі Оz із наступним дзеркальним відображенням у площині хОу (дзеркально-поворотна вісь).
2.14.Знайти матрицю переходу для двох послідовних поворо-
тів на кут ϕ навколо осі Оz та кут θ навколо осі Оу'.
2.15. Знайти матрицю переходу для дзеркального відобра-
ження в площині, |
перпендикулярній вектору: а) (0, 0, 1); |
б) (1, 1, 0); в) (1, 1, 1); г) |
n, де n = 1. |
2.16. Знайти матрицю переходу для повороту системи координат на кут ϕ навколо осі, паралельної вектору: а) (1, 1, 1);
б) n , де n = 1.
2.17. Знайти матрицю переходу для нескінченно малого повороту на кут δϕ = n δϕ , де n – одиничний вектор, який задає на-
прямок осі.
2.18. За яких умов наведені матриці переходу перетворюють
ортонормований базис |
в ортонормований: а) αij |
= 2aia j −δij ; |
б) αij = aiaj −εijk ak ; в) αij = β(aiaj −εijk ak −δij ). Тут ai |
( i = 1, 2,3 ) – |
|
компоненти вектора a, |
β – число. |
|
|
23 |
|
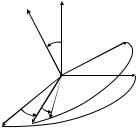
2.19. Знайти матрицю переходу для |
|
x3′ |
|
x3 |
||
повороту на три кути Ейлера ψ, θ, ϕ |
|
|
|
x2′ |
||
(послідовність поворотів: навколо осі |
|
|
θ |
|||
х3 на кут ψ (після такого повороту вісь |
|
|
|
|||
|
|
|
|
|||
х1 переходить в ON), навколо лінії ON |
|
|
O |
x2 |
||
− на кут θ, навколо осі x3′ |
− на кут ϕ) |
|
ψ |
ϕ |
|
|
(рис. 2.6). (Лінія ON визначає перетин |
|
|
||||
|
|
|
|
|||
площин х1Ох2 та x′Ox′ |
). |
|
x1 |
N |
x′ |
|
1 2 |
ei |
системи S |
|
1 |
|
|
2.20. Виразити орти |
|
|
Рис. 2.6 |
|||
через орти ei′ системи S' та кути Ейлера (див. задачу 2.19). |
||||||
2.21. Виразити орти ei′ |
системи S' через орти ei |
системи S та |
||||
кути Ейлера (див. задачу 2.19).
2.22.Використовуючи явний вираз для матриці переходу, до-
вести, що для просторового повороту навколо осі Ох (осі Оy, або Оz) має місце групова властивість A(ϕ1) A(ϕ2 ) = A(ϕ1 +ϕ2 ) .
2.23.Довести на прикладах, що результат двох послідовних поворотів навколо різних осей залежить від порядку їх виконання.
2.24*. Знайти напрямок c та кут θc повороту навколо нього, який еквівалентний двом послідовним поворотам навколо напрямків a і b на кути θa та θb, відповідно.
|
2.25. Який зміст мають перетворення простору r → r′ вигля- |
||||||
ду |
xi′ = Aij x j , задані матрицями: а) |
A = λE , де λ – додатне чис- |
|||||
ло, E – одинична матриця; б) |
A = E + a a , де a – довільний |
||||||
вектор; в) A = 2n n − E , |
де |
|
n – |
одиничний |
вектор; |
||
г) |
A = E + a b , де вектори |
a |
і |
b |
перпендикулярні; |
||
д) |
A = e1′ e1 + e2′ e2 + e3′ e3 , |
де |
e1 , e2 , |
e3 |
та e1′, e2′ , |
e3′ – дві |
|
трійки взаємно перпендикулярних одиничних векторів.
24

Розділ 3 Перетворення векторів і тензорів при заміні базису
Закон перетворення компонент вектора (прямий та обернений)
за ортогональних перетворень системи координат має вигляд |
|
ai′ = αija j , ai = αjia′j , |
(3.1) |
тобто компоненти вектора перетворюються за тим самим законом, що й відповідні базисні вектори (2.1) та (2.4) або декартові координати (2.6)5. Закон перетворення вектора зручно подати у матричній формі:
a |
′ |
= Aa, |
T ′ |
(3.2) |
|
a = A a . |
|
Закон перетворення тензора другого рангу t із компонентами
tij (пишуть t ={tij }, |
говорять "тензор tij ", матрицю компонент |
||||||||
тензора позначають |
|
|
tij |
|
|
|
) |
за ортогональних перетворень систе- |
|
|
|
|
|
||||||
ми координат має вигляд |
|
|
|||||||
|
tij = αik αjltkl , tij = αkiαljtkl . |
|
|||||||
|
|
′ |
′ |
(3.3) |
|||||
У матричній формі закон перетворення тензора другого рангу (3.3) можна подати як
t |
′ |
T |
T ′ |
(3.4) |
|
= AtA , |
t = A t A. |
|
Для тензорів вищих рангів закон перетворення компонент за ортогональних перетворень систем координат можна записати
аналогічно, зокрема для тензора третього рангу маємо |
|
λ′ijk = αilαjmαknλlmn , λijk = αliαmjαnkλ′lmn . |
(3.5) |
Компоненти тензора другого рангу у новій системі координат можна шукати, перемножуючи матриці за однією із формул (3.4). Для тензорів вищих рангів такої можливості у загальному випадку немає. Тому залишається покомпонентно розписувати суми типу (3.5).
Однак існує інша можливість, яка дає особливо ефективний спосіб розв'язку тоді, коли задача полягає в знаходженні не всього тензора, а лише деяких його компонент, або коли матри-
5тому декартові координати точки утворюють вектор, який називають радіусвектором цієї точки.
25
ця переходу проста та має велику кількість нульових елементів. Метод ґрунтується на результатах задачі 3.5: компоненти тензора перетворюються за таким самим законом, що й добутки відповідних координат вектора (зауважимо, що порядок множників принциповий, якщо тензор не є симетричним відносно перестановки відповідних індексів). Наприклад, компонента тензора λ1231 перетворюється за таким самим законом, що і добуток х1х2х3х1. Таким чином, маючи закон перетворення декартових координат вектора, складаємо відповідні добутки нештрихованих координат, виражаючи їх через добутки штрихованих (або навпаки) і зберігаючи порядок множників до розкриття дужок. Закон перетворення відповідної компоненти тензора записуємо за аналогією (із тими самими коефіцієнтами розкладання), замінивши добутки декартових координат на компоненти тензора із відповідними індексами, наприклад x2′x3′x1′x1′ – на компоненту
λ′2311 (див. розв'язок задачі 3.7). Зауважимо, що при цьому немає потреби у знаходженні матриці переходу в явному вигляді.
3.1. Записати закон перетворення компонент вектора a = (a1, a2 , a3 ): а) при повороті системи координат на кут ϕ на-
вколо осі Oz проти годинникової стрілки; б) за інверсії. Виконати аналогічне обчислення для компонент векторного
добутку a ×b . Порівняти результати.
3.2. Знайти закон перетворення компонент вектораa = (1, 2,3)
для послідовних перетворень системи координат: поворот на кут π/6 навколо осі Oz, далі – на кут π/2 навколо осі Ох' так, щоб вісь Оy' збігалася з Oz.
3.3. Задано вектор a = (a1, a2 , a3 ) . Знайти послідовність двох
поворотів системи координат навколо координатних осей, у результаті яких a = (0,0, a3′) . Чому дорівнює a3′?
|
|
I |
0 |
0 |
|
|
3.4. Знайти компоненти тензора |
|
1 |
I2 |
0 |
|
у системі ко- |
I = |
0 |
|
||||
|
|
|
0 |
I3 |
|
|
|
0 |
|
|
|||
ординат, повернутій на кут ϕ відносно осі Ох.
3.5. Показати, що компоненти довільного тензора другого рангу tij перетворюються як добутки декартових координат xi x j .
26
Тут набори (x1, x2 , x3 ) і (x1, x2 , x3 ) – координати двох довільних
точок або компоненти двох довільних радіус-векторів. Результат узагальнити на випадок тензорів вищих рангів.
3.6.Знайти компоненти t11′ , t12′ тензора другого рангу t при перетворенні системи координат x′ = y , y′ = −x , z′ = −z .
3.7.Знайти всі компоненти tij′ тензора t другого рангу загаль-
ного вигляду у системі координат, повернутій на кут π навколо осі Oz.
3.8. Знайти компоненту t12′ симетричного тензора t = {tij} у
системі′ координат, повернутій на кут ϕ навколо осі Oz. Для яких |
|||||
кутів t12 = 0? |
поворот, |
який |
приводить симетричний тензор |
||
3.9. Знайти |
|||||
|
t11 |
t12 |
0 |
|
|
другого рангу |
|
t22 |
0 |
|
до діагонального вигляду. |
t = t12 |
|
||||
|
|
0 |
t |
|
|
|
0 |
|
|
||
|
|
|
33 |
|
|
У задачах 3.10, 3.22–3.27 розглядатимуться так звані матеріальні тензори, що характеризують деяку фізичну систему із заданою симетрією та залишаються інваріантними (тобто матриця, що є зображенням тензора, – незмінна) відносно перетворень, у результаті яких фізична система суміщається сама із собою. Необхідно визначити відмінні від нуля та незалежні компоненти тензора, виразити залежні компоненти через незалежні.
3.10. Знайти обмеження на загальний вигляд тензора t другого рангу, якщо він не змінюється після просторових перетворень:
поворот на кут 2π/2 навколо осі Oz (вісь симетрії С2); поворот на кут 2π/4 навколо осі Oz (вісь симетрії С4); поворот на кут 2π/6 навколо осі Oz (вісь симетрії С6); поворот на кут 2π/8 навколо осі Oz (вісь симетрії С8); віддзеркалення у площині хОу (перетворення σh); є) поворот на кут 2π/2 навколо осей Oх, Oу та Oz.
3.11. Відомо, що у кожній системі координат виконуються співвідношення аі = tijbj, де tij – компоненти тензора другого рангу. Довести необхідну та достатню умову (обернена тензорна ознака): коли величини bi – компоненти вектора, то величини аі також утворюють вектор.
27

3.12. Довести, що об'єкт ∫ xi x j dV є тензором другого рангу,
V
де xi (i = 1, 2, 3) – декартові координати радіус-вектора.
3.13. Розкладання вектора a за векторами циклічного базису6 e± = ex ±iey , e0 = ez
має вигляд a = 12 (a+e− + a−e+ ) + a0e0 . Виразити циклічні компо-
ненти вектора a± , a0 через декартові.
3.14. Циклічний базис і циклічні координати вектора означені в задачі 3.13: а) знайти співвідношення ортогональності та попарні векторні добутки векторів циклічного базису; б) виразити скаляр-
ний a b і векторний a ×b добутки через циклічні компоненти співмножників; в) знайти закон перетворення компонент a± , a0 при повороті системи координат навколо осі Oz на кут ϕ.
3.15*. Циклічними |
компонентами |
симетричного тензора |
|||||
(tij = tji) називаються величини |
|
|
|
|
|||
t++ = t11 |
−t22 |
+ 2it12 |
, |
t00 |
= t33 , |
= t13 |
+it23 , |
t−− = t11 |
−t22 |
− 2it12 |
, |
t0+ |
= t+0 |
||
t+− = t−+ = t11 +t22 , |
|
t0− |
= t−0 |
= t13 |
−it23. |
||
Записати закон перетворення циклічних компонент тензора t при повороті системи координат навколо осі Oz на кут ϕ.
3.16*. Знайти закон перетворення циклічних компонент вектора при поворотах системи координат на всі кути Ейлера (див.
задачу 2.19).
3.17.Записати закон перетворення компонент тензора t при повороті системи координат на кут ϕ навколо осі Oz. Розкласти тензор t на симетричну та антисиметричну частини. Довести, що вони є тензорами.
3.18.Антисиметричний тензор Ω другого рангу можна подати
увигляді
|
|
0 |
−ω3 |
ω2 |
|
Ω = |
|
ω |
0 |
−ω |
. |
|
|
3 |
|
1 |
|
|
|
−ω2 |
ω1 |
0 |
|
|
|
|
6Циклічний базис зручний за опису векторів, що обертаються, зокрема, для частинок у магнітному полі, світла циркулярної поляризації тощо.
28
Довести, що величини ω1, ω2, ω3 утворюють аксіальний вектор ω. Виходячи із закону перетворення компонент тензора Ω, знайти закон перетворення компонент вектора ω за віддзеркалення у площині хОу та інверсії.
3.19.Дано: а та b – тензори другого рангу, між компонентами
яких існує лінійний зв'язок вигляду aij = λijklbkl. Довести, що величини λijkl утворюють тензор четвертого рангу.
3.20.Знайти компоненту λ123′ тензора λ третього рангу у сис-
темі координат, отриманій поворотом на кут π/4 навколо осі Ох. 3.21. Знайти число незалежних компонент тензора t = {tijk } у
n-вимірному просторі, якщо він абсолютно: а) симетричний; б) антисиметричний.
3.22.Знайти відмінні від нуля компоненти λ тензора четвертого рангу, якщо він не змінюється при повороті на кут π навколо осі Оz.
3.23.Визначити число незалежних компонент тензора пруж-
них сталих λ = {λijkl } , що задовольняє властивості симетрії:
λijkl = λklij, λijkl = λjikl, λijkl = λijlk.
3.24*. Компоненти тензора λ четвертого рангу задовольняють
рівності: λijkl = λklij, λijkl = λjikl, λijkl = λijlk. Які компоненти тензора λ відмінні від нуля, якщо він не змінюється при повороті на
кут π/2 навколо осей Ох, Оу та Оz? Знайти незалежні компоненти тензора λ.
3.25*. Компоненти тензора λ четвертого рангу задовольняють рівності λijkl = λklij , λijkl = λ jikl , λijkl = λijlk . Які компоненти тен-
зора λ відмінні від нуля, якщо він не змінюється при повороті на довільний кут навколо осей Ох, Оу та Оz?
3.26. Показати, що тензор λ = {λijkl } пружних сталих ізотроп-
ного тіла характеризується двома незалежними параметрами. 3.27. Визначити число незалежних компонент тензора
λ = {λijkl } пружних сталих кристалу: а) кубічної симетрії C4; б) гексагональної симетрії C6 (вісь симетрії – Оz).
29

Розділ 4 Алгебраїчні операції над тензорами
Якщо за допомогою якої-небудь операції із одного або кількох тензорів утворюються інші, то такі операції називаються тензорними. За координатного підходу всі тензорні операції визначаються через компоненти тензорів, але мають інваріантний зміст, тобто означені співвідношення між компонентами тензорів виконуються у будь-якій системі координат.
Додавання (віднімання). Якщо А та В – тензори рангу n, то їх
сумою (різницею) називається тензор С рангу n із компонентами
Ci1…in = Ai1…in + Bi1…in (Ci1…in = Ai1…in − Bi1…in ).
Зауважимо, що додавати (віднімати) можна тільки тензори одного рангу7.
Множення. Зовнішнім (тензорним) добутком тензора A={Ai1i2…in }
рангу n із тензором B = {B j1 j2…jm } рангу m називається тензор С
рангу n + m із компонентами Ci1i2…in j1 j2…jm = Ai1i2…in Bj1 j2…jm . Тензори-співмножники, на відміну від доданків у сумі (різни-
ці), можуть бути різного рангу. Наприклад, якщо А – тензор першого рангу (вектор), В – тензор другого рангу, то їх тензорним добутком є тензор С третього рангу із компонентами Cijk = Ai Bjk .
За інваріантного запису ця операція звичайно позначається знаком або іноді без символу множення. Для наведеного вище прикладу A B ≡ AB ≡{Ai B jk } . Зовнішній добуток тензорів – це
спосіб побудови тензорів вищих рангів.
Як й у випадку множення матриць, добуток тензорів є асоціативним A (B C) = ( A B) C, і, загалом кажучи, некому-
тативним A B ≠ B A.
У випадку векторів a та b їх тензорний добуток
часто називають прямим добутком векторів, а сам тензор a b ще називають діадою.
7Нульовий тензор довільного рангу позначається символом 0.
30
