
ovta-zbirnyk-zadach
.pdf3.25. Дві лінійно незалежні компоненти. Відповідь до задачі 3.24 доповнюється додатковою умовою λ1111 – λ1122 = 2 λ1212.
3.27. а) три компоненти, λ1111 = λ2222 = λ3333 = α,
λ1122 = λ1133 = λ2233 = β, λ1212 = λ1313 = λ2323 = γ, б) п'ять компонент, λ1111 = λ2222, λ3333, λ1122, λ1133 = λ2233,
λ1313 = λ2323, λ1212 = (λ1111 – λ1122)/2.
Алгебраїчні операції над тензорами
4.2. Указівка: показати, що tijk |
= −tijk . |
|
|
|
|
|||||||||||
4.3. Указівка: умову tik a jk |
= δij |
переписати у матричній формі. |
||||||||||||||
|
|
|
|
4 |
5 |
|
6 |
|
|
4 |
8 |
|
12 |
|
||
4.7. |
a b = |
|
8 10 12 |
|
|
|
5 10 15 |
. |
||||||||
|
|
|
, b a = |
|
||||||||||||
|
|
|
|
|
12 |
15 |
18 |
|
|
|
6 |
12 |
18 |
|
||
|
|
|
|
|
|
|
|
|
||||||||
4.9. а) |
a (b c ), |
|
б) |
(a b )c , |
|
в) |
b2 a , |
г) 0. |
||||||||
4.10. а) |
t(a + b ) = (a b )(a ± b ) + b2 a ± a 2b , |
|
|
|||||||||||||
|
|
t(a − b ) = (a b )(a b ) − b2 a ± a 2b , |
|
б) 0. |
||||||||||||
4.11. a2 b2 , |
(a b )2 . |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
1 −2 |
|
|
0 −3 5 |
|
|
|||||||
4.12. |
|
|
1 |
|
−5 7 |
|
|
|
3 0 −1 |
|
, |
|
||||
|
S = |
|
, |
|
A = |
|
|
|||||||||
|
|
|
−2 7 |
|
9 |
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
−5 1 |
|
|
|
|
||||||
а) 5; 0; 5; |
|
б) b = (6,12, 36), |
c = (−12,12,42); |
в) 138; |
|
г) 215, 70; |
|||||||||||||||
−2/3 |
|
|
−2 |
|
|
3 |
|
13/3 |
|
|
|
|
|
|
|
|
|
||||
|
4 |
|
−20/3 |
|
6 |
|
|
26/3 |
|
344/3; |
|
є) 28, 8, 42, –26. |
|||||||||
д) |
|
|
, |
|
, |
|
|||||||||||||||
|
−7 |
|
|
|
8 |
|
|
22/3 |
|
|
31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
14 |
|
30 |
|
|
|
|
|
|
|
|
|
−4 2 3 |
9 |
|
|
||||
4.13. а) |
|
32 |
|
|
36 |
|
, 228; б)12,0, |
0; |
в)15,0,15; г) |
|
4 0 6 |
|
|
22 |
|
, 158. |
|||||
|
|
, |
|
|
|
, |
|
||||||||||||||
|
|
|
50 |
|
|
42 |
|
|
|
|
|
|
|
|
|
7 8 4 |
|
|
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
ε11 − ε13ε31/ε33 |
|
ε12 − ε13ε32 /ε33 |
|
0 |
|||||
4.14. 221. |
|
|
|
|
4.15. 0, |
ε21 − ε23ε31/ε33 |
|
ε22 − ε23ε32 /ε33 |
0 . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
101 |
|
|
|
|
|
|
|
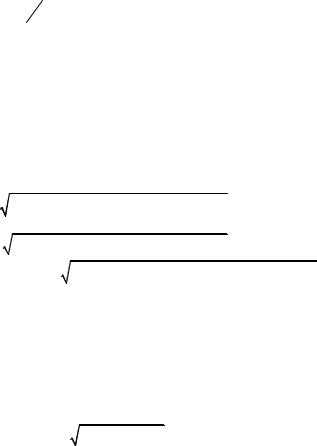
4.16.Еліпсоїд r′T r′= 1 , де Tij = tki−1 tkj−1 , i, j, k = 1, 2,3.
4.17.(b c )(a d ) .
4.18. а) L = ω(0, −I sin α, I3 cos α) , |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
(I3 − I ) sin 2α |
|
|
|
2 |
|
2 |
|
|
||
|
L′ = ω |
0, |
|
|
|
, I sin |
|
α + I3 cos |
|
α |
, |
|||||||
|
|
2 |
|
|
||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
б) |
T = T |
′ |
= |
2 |
ω |
2 |
(I sin |
2 |
α + I3 cos |
2 |
α), |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||||
в) |
N = (I − I3 )ω2 sin α cos αe1 , |
N ′ = (I − I3 )ω2 sin αcos αe1′ . |
||||||||||||||||
4.19. I1 cos2 α + I2 cos2 β + I3 cos2 γ . Указівка: Inn = n I n – момент інерції відносно осі, що задається одиничним вектором n.
4.20. 2m(a 2b2 + b2 c2 + c2 a 2 ) , де m – маса паралелепіпеда.
3(a 2 + b2 + c2 )
Указівка: скористатись результатом задачі 4.19.
4.21.I xy = I1 , I xz = I yz = ( I1 + I3 )/2 .
4.22.а) σ = nσn = σ1nx2 +σ2n2y +σ3nz2 = σ1 cos2 α+σ2 cos2 β+σ3 cos2 γ ,
б) |
j = (σ cos α)2 |
+ (σ |
2 |
cosβ)2 + (σ |
3 |
cos γ)2 E, |
|
||||||
|
1 |
|
σ |
|
|
|
|
|
|
||||
cos θ = |
|
|
|
|
|
|
|
|
, |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
(σ cos α)2 |
|
|
|
cos β)2 + (σ |
|
|
|
|
|||||
|
|
+ (σ |
2 |
3 |
cos γ)2 |
|
|
||||||
|
1 |
|
|
|
|
|
|
|
|
|
|||
в) |
j = σE , j = (σ cos α)2 + (σ |
2 |
cosβ)2 + (σ |
3 |
cos γ)2 −σ2 E . |
||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
||
4.23. Указівка: урахувати Iωω = ωI ω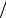 (ω ω) та записати вираз для
(ω ω) та записати вираз для
кінетичної енергії, використовуючи формулу Ейлера.
4.24. Указівка: переписати співвідношення в індексній формі й використати означення симетричного (антисиметричного) тензора.
4.25. Див. задачу 4.24. 4.26. Tij = t ji , де i, j = 1, 2,3. 4.27. a b.
4.28.Указівка: вираз для тензора С записати в індексній формі.
4.29.t = En2 −n n .
4.30. |
|
u |
|
= |
|
v |
|
, |
|
μ |
|
= a2b2 − (a b )2 . Вектори a × b , |
u та v утво- |
||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
||||||||||||||||||
рюють праву (ліву) трійку векторів, якщо μ = |
|
μ |
|
( μ = − |
|
μ |
|
). |
|||||||||||||
|
|
|
|
||||||||||||||||||
4.31. a = te1 , b = te2 , c = te3 , або a = e1t , b = e2 t , |
c = e3 t . |
||||||||||||||||||||
102 |
|
|
|
|
|
|
|
|
|
||||||||||||

4.32. Указівка: для доведення компланарності всіх векторів tu скористатись розкладанням вектора u на повздовжню та поперечну складові відносно вектора v; усі вектори, ортогональні до v, – компланарні.
4.34. Указівка: довільний вектор завжди можна розкласти за трійкою некомпланарних векторів.
4.35. A a* + B b* + C c* , де вектори a*, b * , c* взаємні до векторів a, b , c .
4.36. Указівка: записати результат дії правої частини тотожності на αa +βb + γc , де α,β, γ – довільні числа.
4.37. (b × c ) e1 + (c × a ) e2 + (a ×b ) e3 .
4.38. t−1 = a * e |
+ b * e |
+ c * e , |
t−1 = e a *+e |
|
b *+e c *, де |
|||||
|
1 |
1 |
2 |
3 |
2 |
1 |
2 |
|
3 |
|
вектори a*, b * , |
c* взаємні до векторів a, b , c. |
|
|
|||||||
4.40. λijkl = αδijδkl +βδik δjl + γδilδjk , |
а) αδijukk |
+βuij + γu ji , |
||||||||
б) αδij ukk + (β + γ)uij , в) (β − γ)uij ; г) (3α + β + γ)δij . |
|
|||||||||
4.41. Загальний випадок λijkl = Aδij δkl + Bδik δ jl |
+ C δil δ jk , |
|||||||||
а) |
λijkl |
= Aδijδkl |
+ B(δik δjl + δil δjk ), |
|
|
|
|
|
||
б) |
λijkl |
= A( 1 2 (δik δ jl + δil δ jk ) − 13 δij δkl ), |
λijkl = 0, |
|
||||||
в) |
λijkl |
= A(δij δkl |
+ δik δ jl |
+ δil δ jk ), |
|
г) |
|
|||
д) |
λijkl |
= A(δik δ jl − δil δ jk ). |
|
|
|
|
|
|
||
4.43. Відповідь: за такого повороту відносне розташування вектора s і координатних осей (яке може бути задане, напр., кутами між координатними осями та вектором s ) не змінюється, не
змінюються й координати вектора s , отже – і компоненти тен-
зора sisj.
4.44. Відповідь: а) εij = Aδij + Bsi s j , тензор є одновісним як лінійна
комбінація ізотропного та одновісного тензорів (див. задачі 4.39
та 4.43); б) εij = B(si s j − 1 3 δij ) .
4.45. Указівка: показати, що довільний симетричний одновісний тензор рангу два має дві незалежні компоненти, які можна вира-
103
зити через головні значення тензора, тобто діагональні компоненти тензора в головній системі координат.
4.46. δij δkl , δik δ jl , δil δ jk ,
|
δij sk sl , δik s j sl , δil s j sk , δ jk si sl , δ jl si sk , δkl si s j , |
si s j sk sl . |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4.47. а) |
|
ηijkl |
|
= A(δij δkl |
|
+ δik δ jl |
+ δil δ jk ) + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
+ B(δ s s +δ s |
|
s +δ s |
s +δ |
|
s s +δ |
s s +δ |
|
|
s s |
j |
) +Cs s |
s s , |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ij k l |
|
|
ik |
j l |
|
|
|
il |
|
|
j k |
|
|
|
|
jk i l |
|
|
|
|
jl i k |
|
|
|
kl i |
|
|
|
|
|
|
i |
|
j k l |
|||||||||||||||||||||||||||||||
б) |
|
|
ηijkl = Aδijδkl + D(δik δjl + δilδjk ) + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
+B(δ s s +δ s s |
j |
) +F(δ s |
|
s +δ s s +δ |
s s +δ |
|
s s ) +Cs s s s . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ij k l |
|
|
|
kl i |
|
|
|
|
|
|
|
|
ik |
|
j l |
|
|
|
il j k |
|
|
|
|
jk i l |
|
|
|
|
jl i k |
|
|
|
|
|
i j k l |
|||||||||||||||||||||||||||||||
4.48. η |
ijkl |
= |
1 |
3 |
λ (δ |
ij |
δ |
kl |
+ δ |
ik |
δ |
jl |
+ δ |
il |
δ |
jk |
) |
+ (λ |
1 |
+ λ |
3 |
− 6λ |
2 |
)s s |
j |
s |
k |
s + |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
l |
|||||||||||||||||||||||||||
+(λ3 − 13 λ1 )(δij sk sl + δik s j sl + δil s j sk + δ jk si sl + δ jl si sk + δkl si s j ) . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
= 0, |
|
|
=δ/3, |
|
|
|
=0, |
|
|
|
|
|
|
|
= (δ δ |
+δ δ |
|
|
+δ |
|
|
δ )/15. |
||||||||||||||||||||||||||||||||||||||||||
4.49. |
|
n |
nn |
nn |
n |
n n |
j |
n n |
jl |
|
jk |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
i |
|
|
|
|
|
|
i j |
ij |
|
|
i j |
|
k |
|
|
|
|
|
|
|
i |
|
|
k |
l |
|
|
ij kl |
|
|
|
ik |
|
|
|
|
|
il |
|
|
|
|
|
||||||||||||||||||||||
4.50. а) |
|
|
|
1 |
3 |
a2 ; |
б) |
|
1 |
3 |
|
(a b); |
|
|
|
в) |
|
|
|
1 |
3 |
a; |
|
г) |
2 |
3 |
a2 ; |
|
д) |
2 |
3 |
(a b); |
|||||||||||||||||||||||||||||||||||
є) 115 ((a b )(c d ) + (a c )(b d ) + (a d )(b c ) ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
4.51. Оскільки протилежні орієнтації вектора |
|
|
s |
рівноймовірні, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
то тензори непарних рангів дорівнюють нулю: |
|
= 0 , |
|
|
|
= 0 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
si |
si s j sk |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Тензор |
|
|
|
є симетричним та одновісним щодо напрямку век- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
si s j |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
тора n . Позначивши |
|
|
|
|
|
|
через |
|
εij , |
|
відповідно до результатів |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
si s j |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
задач 4.44 і 4.45, маємо |
|
εij |
= ε1δij + (ε3 − ε1 )ni n j , |
де |
ε1 = |
sx2 |
= |
s2y |
, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ε3 = |
sz2 |
|
|
у системі координат із віссю Oz, |
паралельною до s. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Крім того, |
|
s 2 |
= 1 , |
тому |
|
sx2 |
+ |
s2y |
+ |
sz2 |
= 2ε1 + ε3 = 1 . Отже, |
|
головні |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
значення тензора |
|
|
|
|
|
задаються одним незалежним парамет- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
si s j |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ром, який залежить від вигляду функції розподілу f (θ).
У подібних випадках, зокрема у теорії нематичних рідких кристалів, використовують наступне розкладання функції роз-
поділу, що залежить тільки від сферичного кута θ:
∞
f (θ) = ∑ (2l +1)Sl Pl (cos θ)
l =0
за поліномами Лежандра Pl (cos θ) , які утворюють систему ортогональних на одиничній сфері функцій,
104

|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
∫ |
P′(cos θ)P (cos θ) sin θd θ = |
|
|
δ ′ . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
l |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
2l +1 |
l l |
||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
У розкладанні функції розподілу f(θ) коефіцієнти |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
S |
|
= |
1 |
π |
f (θ) P (cos θ) sin θd θ |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
l |
|
|
2 |
∫ |
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
, де |
|
|
– так звані параметри порядку, Sl |
= |
|
|
|||||||||||||||||||||||||||
Pl (cos θ) |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 π |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
π |
∫ |
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
P (cos θ) = |
1 |
|
|
d ϕ |
|
P |
|
(cos θ) f (θ) sin θd θ . |
|||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 1 |
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
= 1 |
|
|
|
|
|
|
||||
Зокрема, |
S |
2 |
2 |
(3cos2 θ −1), |
|
|
S |
4 |
8 |
(35cos4 |
θ − 30cos2 θ + 3), |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
s4 = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
звідки s2 |
= 1 |
3 |
(1 |
+ |
2S |
2 |
), |
35 |
(8S |
4 |
+ |
20S |
2 |
+ 7). Тоді остаточно |
||||||||||||||||
z |
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
||||||||
si s j = 13 δij + S2 |
(ni n j |
− 13 δij ). Частина цього тензора, пропор- |
||||||||||||||||||||||||||||
ційна параметру порядку, є тензором із нульовим слідом (див. задачу 4.44 б). У випадку сферично симетричного розподілу, коли f (θ) =1 і S2 = 0, ця частина зникає, отримуємо результат за-
дачі 4.49. Навпаки, якщо вектор s орієнтований строго вздовж n , маємо S2 =1, тоді si s j = ni n j .
Тензор si s j sk sl є повністю симетричним тензором четвертого рангу, крім того, він є одновісним відносно напрямку вектора
n , |
отже має загальний вигляд, отриманий у задачі 4.48. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
s |
s |
j |
s |
k |
s |
l |
= 1 |
3 |
λ |
1 |
(δ |
ij |
δ |
kl |
+ δ |
ik |
δ |
jl |
+ δ |
il |
δ |
jk |
) + (λ |
1 |
+ λ |
3 |
− 6λ |
2 |
)n |
n |
j |
n |
k |
n |
l |
+ |
||||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
||||||||||||||||||
+(λ3 − 13 λ1 )(δij nk nl + δik n j nl + δil n j nk + δjk ninl + δjl nink + δkl nin j ) , |
||||||||||||||||||||||||||||||||||||||||
де λ1 = |
sx4 |
, |
λ2 |
|
= |
sx2 sz2 |
, λ3 = |
sz4 |
. Ураховуючи, що вектор s |
|
– оди- |
|||||||||||||||||||||||||||||
ничний, після усереднення за кутом ϕ отримаємо, що всі середні
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
значення |
s s |
j |
виражаються через два незалежні параметри s2 та |
|||||||||||
|
|
|
i |
|
|
|
|
|
|
|
z |
|||
|
|
: sx2 = 12(1− sz2 ) , λ3 = |
|
, λ2 = 12 (sz2 − sz4 ), λ1 = 3 8 (1 − 2 sz2 + sz4 ). |
||||||||||
|
sz4 |
sz4 |
||||||||||||
|
|
|
можна виразити через параметри порядку |
|||||||||||
У свою чергу, |
|
sz2 |
і |
sz4 |
||||||||||
S2 і S4.
4.52. Усереднення за об'ємом еквівалентне усередненню за орієнтаціями, оскільки розміри мікрокристалів однакові. Нехай напрямок осі симетрії окремого мікрокристала задається вектором
105
s (протилежні орієнтації вектора s еквівалентні). У гексагональному кристалі симетричний тензор другого рангу є одновісним і має вигляд εij = ε1δij + (ε3 − ε1 )si s j (див. задачу 4.45), а повністю симетричний тензор четвертого рангу мікрокристалів за
заданого s |
|
стає одновісним після усереднення за орієнтаціями |
|||||||||||||||||||||||||||||
кристалічних осей, |
перпендикулярних до s , |
і має вигляд (див. |
|||||||||||||||||||||||||||||
задачу 4.48) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
η |
ijkl |
= 1 |
3 |
λ |
1 |
(δ |
ij |
δ |
kl |
+ δ |
ik |
δ |
jl |
+ δ |
il |
δ |
jk |
) + (λ |
1 |
+ λ |
3 |
− 6λ |
2 |
)s |
s |
j |
s |
k |
s |
l |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|||||||||||||||
+(λ3 − 13 λ1 )(δij sk sl + δik s j sl + δil s j sk + δ jk si sl + δ jl si sk + δkl si s j ) . |
|||||||||||||||||||||||||||||||
Незалежні компоненти цього тензора λ1, λ2, λ3 вважатимемо заданими. Позначимо компоненти тензора для середовища через ςijkl , ςijkl = ηijkl . Скориставшись результатом задачі 4.51, після
усереднення за орієнтаціями вектора s, дістанемо
ε |
ij |
= 1 |
3 |
(2ε + ε |
3 |
)δ |
ij |
+ S |
2 |
(ε |
3 |
− ε |
1 |
)(n |
n |
j |
− 1 |
3 |
δ |
ij |
) , |
|
|
1 |
|
|
|
|
i |
|
|
|
|
||||||||||
ςijkl |
= 13 μ1 (δij δkl |
+ δik δ jl |
+ δil δ jk |
) + (μ1 + μ3 − 6μ2 )ni n j nk nl + |
|||||||||||||||||
+(μ3 − 13 μ1 )(δij nk nl + δik n j nl + δil n j nk + δjk ninl + δjl ni nk + δkl ni n j ). |
|||||||||||||||||||||
Тут μ1 = λ1 + (3λ2 − λ1 )2sx2 + (λ1 + λ3 − 6λ2 )sx4 ,
3μ2 = λ1 + (3λ2 − λ1 )(sx2 + sz2 ) + 3(λ1 + λ3 − 6λ2 )sx2 sz2 ,
μ3 = λ1 + (3λ2 − λ1 )2 sz2 + (λ1 + λ3 − 6λ2 )sz4 ,
а всі середні в правих частинах обраховані в задачі 4.51.
Головні осі тензора. Інваріанти тензора
5.1. λ1,2 |
= |
t11 +t22 |
± |
t11 −t22 |
2 |
+(t12 ) |
2 |
, тензор діагоналізується |
|
|
|
|
|
|
|||||
2 |
2 |
|
|||||||
|
|
|
|
|
|
|
|
||
поворотом навколо осі Oz |
на кут |
ϕ = 1 |
2t12 |
. |
|
2 arctg t −t |
22 |
||||
|
|
|
11 |
|
|
5.2. Указівка: діагоналізувати тензор поворотом навколо осі Oz
на кут ϕ = 1 2 arctg 2−t12 . Власні значення
t11 t22
106

λ1,2 |
= |
t11 +t22 |
± |
t11 −t22 |
2 |
+(t12 ) |
2 |
, |
λ3 = t33 . |
|
|
|
|
|
|
||||||
2 |
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
||
5.4. Власні вектори a1 та a2 , які відповідають комплексно спряженим власним значенням λ1 і λ2 ( λ1 = λ*2 ), задовольняють спів-
відношення a |
a |
* = 0 , |
a a |
2 |
= 1 , |
a |
2 |
= a |
*. |
|
|
|||
|
1 |
|
2 |
|
1 |
|
|
|
1 |
|
|
|||
5.5. а) λ1 = 1 , λ2,3 = 3 ± |
10 ; |
x1 = (1,0,0) |
, |
x2,3 |
= (0, 3,1 ± |
10 ) ; |
||||||||
б) |
λ1 = 3 , λ2,3 = (3 ± |
17 )/2; |
x1 = (0,0,1) |
, |
x2,3 |
= (4,1 ± 17 , 0) ; |
||||||||
в) |
λ1 = 1 , λ2,3 = 1 ± |
3 ; x1 = (1, −1,1) , |
x2,3 |
|
= (2 3,1, −1 ± |
3 ) ; |
||||||||
г) |
λ1=4, λ2,3 = (5 ±3 |
5)/2; x1 =(2,−2,1), |
x2,3 = (−5 ±3 5, 2,14 6 5); |
|||||||||||
д) |
λ1,2 = 1, λ3 = 4; x3 = (1,1,1) , для дійсного симетричного тен- |
|||||||||||||
зора із власними значеннями, що збігаються, λ1 = λ2 , довільний
вектор, що лежить у площині, яка перпендикулярна до власного вектора x3 , буде власним;
є) λ1 = 0, λ2 =1, λ3 = 4 ; x1 = (1,1,0) , |
x2 = (1, −1,1) , |
x3 = (−1,1, 2) . |
|||||||||||||||||||||||||||||||||||||
5.6. λ |
|
= 0 , |
|
λ |
2 |
= 1, |
λ |
3 |
= 4, |
|
x R = 1 |
|
|
(−2,1, 0) , |
|
x R |
= (0,0,1) , |
||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
5 |
|
|
|
|
|
|
2 |
|
|
|
|
||||
xR = |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x L |
|
|
|
|
|
|
= 1 |
|
|
|
|
||||
|
|
|
(2,1,0); |
xL = |
1 |
|
(−1, 2,0) , |
= (0, 0,1) , |
xL |
|
(1,2,0) . |
||||||||||||||||||||||||||||
3 |
|
|
5 |
|
|
|
|
|
|
|
1 |
|
|
|
5 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
5 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5.7. Для всіх матриць λ1 |
= –1, λ2 |
|
= 1. Власні вектори для σ1: |
||||||||||||||||||||||||||||||||||||
x = 1 |
|
|
(1, −1) , |
x |
|
= |
1 |
|
|
|
(1,1) ; для σ2: |
|
x = |
1 |
|
(i,1) |
, x = (−i,1) ; |
||||||||||||||||||||||
1 |
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
для σ3: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
x1 = (0,1) , |
|
x2 = (1, 0) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
5.8. λ |
|
= ± |
1 |
; |
|
|
|
|
|
|
1 |
|
|
|
|
|
iϕ θ |
|
, |
|
|
|
|
1 |
|
|
|
|
iϕ |
|
θ |
. |
|||||||
± |
|
x |
|
= |
|
|
|
|
|
|
|
1,e tg |
|
|
x |
= |
|
|
|
|
1, |
− |
e ctg |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
+ |
|
|
cos(θ/2) |
|
|
|
|
2 |
|
|
− |
|
sin(θ/2) |
|
|
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||||||
5.9. λ |
|
|
= 1, |
|
λ |
3,4 |
|
= −1; |
e = |
|
|
(1, 0, 0,1) , |
e |
|
= |
|
(0,1,1, 0) , |
||||||||||||||||||||||
1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
e = |
|
|
|
(−1, 0, 0,1), |
e |
4 |
= |
|
|
|
(0, −1,1, 0); |
довільна лінійна ком- |
|||||||||||||||||||||||||||
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
бінація векторів e1 і e2 , а також векторів e3 і e4 |
буде власним |
||||||||||||||||||||||||||||||||||||||
вектором. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
107

|
|
|
sin 2 ϕ |
−sin ϕcos ϕ |
0 |
|
|
|
||
5.10. а) ml |
2 |
|
−sin ϕcos ϕ |
cos |
2 |
ϕ |
0 |
|
, |
ϕ − кут між стержнем |
|
|
|
|
івіссю Ox, |
||||||
|
|
|
0 |
0 |
|
1 |
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
б) λ1 = 0, λ2,3 |
= ml2; x |
= (cos ϕ,sin ϕ, 0) |
, x = (− sin ϕ,cos ϕ,0) , |
|
1 |
|
2 |
x3 = (0, 0,1) ; вектори x2 , |
x3 вибираються неоднозначно, довіль- |
||
ний вектор, що лежить у площині, перпендикулярній x1 , буде
|
|
0 |
0 |
0 |
|
|
власним вектором; г) ml |
2 |
|
0 |
1 |
0 |
|
|
|
. |
||||
|
|
|
0 |
0 |
1 |
|
|
|
|
|
|||
5.11. Указівка: скористатися явним виглядом I1 та I2 і розписати
I12 − 2I2 .
5.14. Указівка: використати подання інваріантів тензора через його компоненти tij = ei te j .
5.15. I1 = (a , b , C ) + (a, B, c ) + ( A, b , c ) , (a, b , c )
I2 = ((a, B, C ) + ( A, b , C ) + ( A, B, c ))/(a, b , c ), |
|
I3 = ( A, B, C )/(a , b , c ). |
|||||||||||||||||||||||||
Указівка: t = A a* + B b* +C c* = |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
= |
1 |
|
|
(A (b ×c) + B (c ×a) +C (a ×b)) , |
||||||||||||||||||||
|
|
|
(a,b,c) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I2 |
|
|||||||
|
−1 |
|
|
|
|
* |
|
|
|
|
|
* |
|
|
|
* |
|
−1 |
|
|
|
||||||
t |
|
|
= a A |
+b B |
|
|
+ c C |
|
. Sp t |
|
|
= |
|
|
|
|
. |
||||||||||
|
|
|
|
|
|
|
|
det t |
|||||||||||||||||||
t11 |
t12 |
t13 |
a1 |
b1 |
c1 |
A1 |
B1 |
|
|
C1 |
|
|
|||||||||||||||
|
|
|
t22 |
|
|
|
|
|
b2 |
|
|
|
|
A2 |
B2 |
|
|
|
|
|
випливає рів- |
||||||
Із t21 |
t23 a2 |
c2 = |
|
|
C2 |
||||||||||||||||||||||
t |
31 |
t |
32 |
t |
33 |
a |
3 |
b c |
3 |
|
A B C |
3 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
3 |
|
|
|
|
|
|||||||||
ність det t(a, b , c ) = ( A, B, C ). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
5.16. x , λ2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
i |
|
|
i |
|
|
|
|
|
|
|
|
|
|
x = (0,0,1), |
|
|
|
|
|
|
1 |
(1, ±i, 0). |
|||||
5.17. λ |
= ε , λ |
2,3 |
= ε |
|
± ε |
a |
; |
x |
2,3 |
= |
|
||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
108

5.18. λ1 |
= 0, λ2,3 |
= ± іω; |
x1 |
= |
ω |
, |
|
|
|
|
|
|
|
1 |
|
|
ω×e |
|
|
|
, де |
e |
|
– |
||||||||||||||||||||||||||||||||||||||||||||
ω |
x2,3 = |
|
|
|
|
|
|
|
|
|
|
|
± ie |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
ω× e |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
одиничний |
вектор, |
ортогональний |
до |
вектора |
ω; |
|
|
I1 = 0 , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
I2 = −ω2 , I3 = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
= a |
|
|
|
|
|
|
|
|
|
a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
5.19. λ |
1 |
= a2 , |
|
|
|
|
λ |
2,3 |
= 0; |
|
x |
|
|
|
a |
, |
|
x |
|
|
|
|
Можна |
|
вибрати |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
x2 = |
|
|
|
a ×c |
|
|
|
, |
x3 = |
|
|
a×(a ×c ) |
|
, де c |
– довільний вектор, неколіне- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
a × c |
|
|
|
|
a ×(a × c ) |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
арний із вектором |
|
|
a. |
I1 = a |
2 , |
|
|
|
I2 = I3 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
5.20. λ1 = a b , |
|
λ2,3 = 0; |
|
|
|
|
x1 = a a , |
|
|
x2,3 b. |
|
|
Можна |
|
вибрати |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
|
= |
|
|
|
|
|
c ×b |
|
|
|
, |
|
x |
= |
|
|
b ×(c×b ) |
|
|
, |
|
|
де c |
– довільний вектор, неколіне- |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
c ×b |
|
|
|
|
|
|
|
3 |
|
|
|
b ×(c×b ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
арний |
|
|
|
із |
|
векторами |
|
|
a та b |
|
. |
|
|
|
I1 = a b , І2 = І3 = 0. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
5.21. Див. відповідь до задачі 5.18, де слід покласти ω= b ×a . |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5.22. λ1 = 0, λ |
2,3 |
= a b ± ab; |
|
x = |
a×b |
|
|
, |
|
|
|
|
x |
2 |
= |
|
|
|
|
1 |
|
|
|
|
a + b |
|
, |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
a |
×b |
|
|
|
|
|
|
|
|
|
|
2cos(ϕ/2) a |
b |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
a |
|
|
|
b |
, де ϕ – кут між векторами a та b . |
|
|
|
||||||||||||||||||||||||||||||||||||||||
x3 = |
|
|
|
|
|
|
|
|
a |
− b |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 sin(ϕ/2) |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.23. λ1 = 0, |
|
λ2,3 = ma2; |
|
x1 = a/a , |
|
x2,3 a . |
|
Можна |
|
вибрати |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x2 = |
|
|
|
a ×c |
|
|
|
, |
|
x3 |
= |
|
|
a ×(a × c ) |
|
|
|
, |
де |
c |
|
– довільний вектор, неколі- |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
a × c |
|
|
|
|
|
|
a × (a |
× c ) |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2ma2, І2 = m2a4, І3 = 0. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
неарний із вектором |
a; |
І1 = |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5.24. |
|
|
|
|
|
λ1 = a2 |
2 , λ2,3 = −a2 |
|
2 , x1 = a a , |
|
x2,3 |
|
a . |
|
Вибір |
векторів |
||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
2 |
і |
|
|
|
x |
|
указано у попередній задачі; |
|
|
|
I = −a2 |
, |
I |
2 |
= −a |
4 |
|
, |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
||||
I |
3 |
= a6 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a×b |
|
|
|
|
|
|
|
|
|
|
|
|||||||
5.25. λ1 = 0, λ2 = 1 + cosϕ, λ3 = 1 – cosϕ; x1 = |
|
|
, |
x |
|
= |
|
|
a+b |
|
, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a ×b |
|
2 |
|
|
|
2cos(ϕ/2) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
a −b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x3 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
І1 = 2, І2 = sin |
ϕ, І3 |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
2 |
sin(ϕ/2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
109 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

Тензор Леві-Чівіта
6.2. а) εijk ek ; б) εijk . 6.5. |
a ×b . |
|
|
||||
6.6. S = 1 |
2 |
(a b +b a), |
A = 1 |
2 |
(a b −b a) =ω×E, ω= b ×a |
2 |
. |
|
|
|
|
|
|||
6.7. atb −bta = a(S + A)b −b(S + A)a =2a Ab =2a (ω×E)b =2a (ω×b).
Указівка: використати зв'язок антисиметричної частини А тензора t з аксіальним вектором ω у вигляді Aij = −εijk ωk , де i, j, k = 1, 2, 3.
6.8. Указівка: антисиметрична частина тензора
A = 12 (e1 a − a e1 ) + 12 (e2 b − b e2 ) + 12 (e3 c − c e3 ) =
= 12 (a ×e1 )× E + 12 (b ×e2 )× E + 12 (c ×e3 )× E = ω× E,
де ω= 12 (a ×e1 +b ×e2 + c ×e3 ), E – одинична матриця.
6.9.Указівка: див. попередню задачу.
6.10.Указівка: використати (ei , e j , ek ) = εijk , де i, j, k = 1, 2, 3.
6.11. a) ε′ijk = Δαil α jmαknεlmn ; б) [a′× b′]i = Δαij [a × b ] j , |
= det A |
– визначник матриці переходу. |
добутку |
6.12. а) Ураховуючи формулу для векторного |
|
a × b = εijk aib j ek і тотожність із задачі 6.11, знайдемо |
|
a ×(b ×c ) = εijk ai [b ×c ] j ek = εijk aiεαβjbαcβek = εkijεαβj aibαcβek =
= (δkαδiβ − δiαδkβ )aibαcβek = aibk ciek − aibick ek = b (a c ) − c (a b );
б) b (a c ) − a (b c ); в) (a c )(b d ) − (b c )(a d ); г) b (a, c , d ) − a (b , c , d ) = c (a, b , d ) − d (a, b , c );
д) (b (a c ) − a (b c ))(a , b , c ).
6.13. Указівка: в інтегралі виконати перехід від однієї ПДСК до іншої.
6.14. а) a 2 (b c ) + (a b )(a c ) ; б) (a ×(b ×c )) (a'×(b' ×c')).
Векторні функції скалярного аргументу
7.1. а) 2(r r ) ; б) |
r ×r ; |
в) (r r ) + (r r ) ; |
г) (r r )/ r 2 ; |
д) (r ×r ) (r ×r ) |
(r ×r ) 2 ; є) (r , r , r ) ; ж) r ×(r ×r ) r3 . |
||
|
|
110 |
|
