Ряды Тейлора и Маклорена

Прежде чем говорить о рядах Тейлора выведем формулу Тейлора.

Предположим, что функция имеет все производные до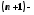го порядка включительно в некотором промежутке, содержащем точку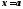. Найдем многочленстепени не выше, значение которого в точкеравняется значению функциив этой точке, а значения его производных дого порядка в точкеравняются значениям соответствующих производных от функциив этой точке

. (13)

Естественно ожидать, что такой многочлен в некотором смысле «близок» к функции .

Будем искать этот многочлен в форме многочлена по степеням с неопределенными коэффициентами

. (14)

Коэффициенты определим так, чтобы удовлетворялись условия (13). Предварительно найдем производные от

(15)

Подставляя в левые и правые части равенства (14) и (15) вместо значениеи заменяя на основании равенства (13)через,черези т.д., получим:

откуда находим

(16)

Подставляя найденные значения в формулу (14), получим

. (17) Обозначим черезразность значений данной функциии построенного многочлена:, откуда, или в развернутом виде

Последнее выражение называется формулой Тейлора.

Допустим, что в рассматриваемой окрестности точки , тогда, переходя к пределу, справа получим бесконечный ряд, который называется рядом Тейлора:(18)

Если в ряде Тейлора положим , то получим частный случай ряда Тейлора, который называется рядом Маклорена:

(19)

На примере покажем разложение функции в ряд Маклорена.

Подставив полученные значения в формулу (19), получим:

Поступая аналогичным образом, получим разложение в ряд Маклорена функций:

Ряды Фурье

Функциональный ряд вида

(20)

называется тригонометрическим рядом, где коэффициенты тригонометрического ряда. Если ряд (20) сходится, то его сумма есть периодическая функцияс периодом, так каки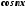являются периодическими функциями с периодом. Таким образом. Определим коэффициенты ряда (20).

Пусть периодическая с функциятакова, что она представляется тригонометрическим рядом, сходящимся к данной функции в интервале, т.е. является суммой этого ряда:

.(21)

Проинтегрируем обе части равенства (21) в пределах от до:

Вычислим отдельно каждый интеграл, встречающийся в правой части:

Следовательно, ,откуда

(22)

Для вычисления остальных коэффициентов ряда нам потребуются некоторые определенные интегралы (доказать самостоятельно). Если и- целые числа, то имеют место следующие равенства:

если 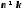, то

(23)

если же , то

(24)

Для определения коэффициента при каком-либо определенном значенииумножим обе части равенства (21) наи проинтегрируем в пределах отдо:

Принимая во внимание формулы (23) и (24), заметим, что все интегралы в правой части равны нулю, кроме интеграла с коэффициентом . Следовательно,

,

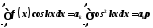откуда

(25)

Умножая обе части равенства (21) на и снова интегрируя в тех же пределах, получим:

,

откуда

(26)

Коэффициенты, определенные по формулам (22), (25), (26) называются коэффициентами Фурье функции, а тригонометрический ряд (20) с такими коэффициентами называетсярядом Фурье функции.

Если периодическая функцияс периодом-кусочно-монотонная и ограниченная на , то ряд Фурье, построенный для этой функции, сходится во всех точках. Сумма полученного рядаравна значению функциив точках непрерывности функции. В точках разрыва функции сумма ряда равняется среднему арифметическому пределов функции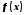справа и слева, т.е. еслиточка разрыва функции, то

.

Периодическая функция обладает свойством, каково бы ни было число, поэтому при вычислении коэффициентов Фурье мы можем заменить промежуток интегрированияпромежутком интегрирования, т.е.

(27)