Дифференциальные уравнения высших порядков

Дифференциальное уравнение го порядка имеет вид:

или, если его можно разрешить относительно ой производной,

Для этих уравнений имеет место теорема о существовании и единственности решения:

Если в уравнении функция и её частные производные по аргументам непрерывны в некоторой области, содержащей значениято существует и притом единственное решениеуравнения, удовлетворяющее условиям

Эти условия называются начальными условиями.

Общим решением дифференциального уравнения го порядка называется функциязависящая отпроизвольных постоянныхи такая, что:

1. она удовлетворяет уравнению при любых значениях постоянных ;

2. при заданных начальных условиях

постоянные можно подобрать так, что функциябудет удовлетворять этим условиям.

Всякая функция, получающаяся из общего решения при конкретных значениях постоянных , называетсячастным решением.

Уравнения вида

Простейшим уравнением го порядка является уравнение вида. Такие уравнения решаются путём интегрирования левой и правой частираз.

. . . . . . . . . . .

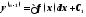
Уравнения второго порядка, приводящиеся к уравнениям первого порядка

1. Уравнения вида , не содержащие явным образом искомой функции, приводятся к уравнениям первого порядка с помощью подстановкигде. Тогдаи данное уравнение примет вид- уравнение первого порядка.

2. Уравнения вида , не содержащие явным образом независимую переменную, приводятся к уравнениям первого порядка с помощью подстановкигде, но, следовательно. Тогдаи данное уравнение примет вид- уравнение первого порядка.

Линейные однородные уравнения. Определения и общие свойства

Определение. Дифференциальное уравнение го порядка называется линейным, если оно первой степени относительно искомой функциии её производныхи имеет вид, гдеи- заданные функции отили постоянные.

Если то уравнение называется неоднородным, если жето уравнение называется линейным однородным уравнением.

Определим некоторые основные свойства линейных однородных уравнений, ограничиваясь уравнениями второго порядка:

1. Если и- два частных решения линейного однородного уравнения второго порядкатоесть также решение этого уравнения.

2. Если есть решение уравненияипостоянная, тоесть также решение этого уравнения.

Определение. Два решения уравнения и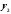называются линейно независимыми на отрезке, если их отношение на этом отрезке не является постоянным, т.е. если.

Определение: Если ифункции от, то определительназывается определителем Вронского.

3. Если , то .

4. Если и- два линейно независимых решения уравнения, тоесть его общее решение, гдепроизвольные постоянные.

Линейные однородные уравнения второго порядка с постоянными коэффициентами

Пусть дано однородное уравнение второго порядка

,(1)

где и- постоянные числа.

Согласно свойству (4) для определения общего решения уравнения надо найти два линейно независимых частных решения. Будем искать частные решения в виде

, где.

Тогда .

Подставим полученные выражения в данное уравнение

,

откуда, т.к. ,(2)

Уравнение (2) называется характеристическим уравнением уравнения (1). Решение уравнения (2) имеет вид:

Возможны следующие случаи:

1. и - действительные и притом не равные между собой;

2. и - действительные и притом равные между собой;

3. и - комплексные числа.

Рассмотрим каждый случай отдельно:

1. 

В этом случае , причёмт.к., следовательно, общее решение по свойству (4) имеет вид

2. 

Одно частное решение можно искать в виде , но второе уже искать в таком же виде нельзя, т.к. они окажутся линейно зависимыми. Второе частное решение будем искать в виде, где. Тогдаи

. Подставим значения в уравнение (1):

.

Т.к. корень характеристического уравнения, то, кроме того, т.к. корни равны между собой. Следовательно,, откуда. Решая последнее уравнение получим. Полагаяполучим. Следовательно, второе частное решение можно искать в виде. Заметим, что. По свойству (4) имеем, т.е.

3. 

В этом случае .. Следовательно,

.

Обозначим и ,тогда по свойству (4) общее решение: